什么是树?

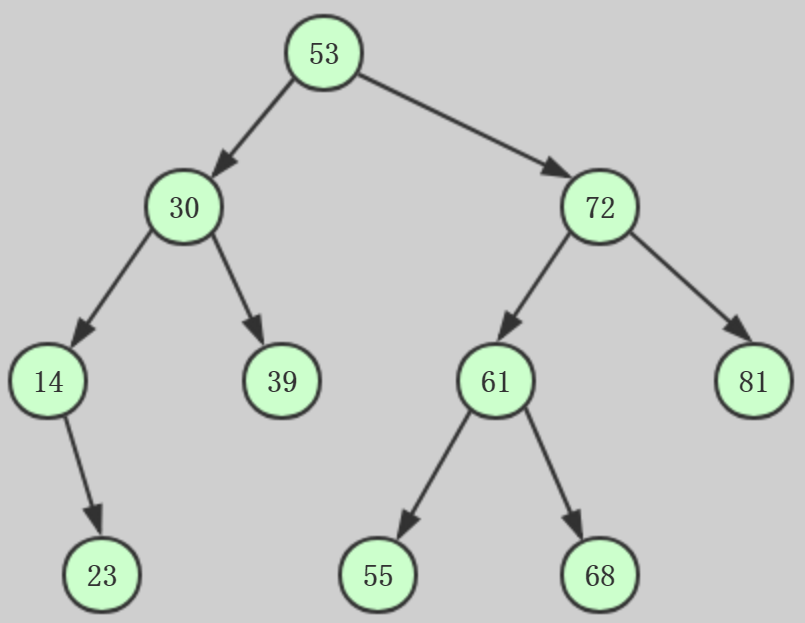
上面图例就是一个树,用圆代表节点,连接圆的直线代表边。树的顶端总有一个节点,通过它连接第二层的节点,然后第二层连向更下一层的节点,以此递推
,所以树的顶端小,底部大。和现实中的树是相反的,但是代码一般从顶点开始执行操作
本文会讲述一种特殊的树--二叉树,每个节点最多有两个子节点。普通的树,节点可以多于两个,称为多路树/多叉树
树的术语:

1、路径:顺着节点的边从一个节点走到另一个节点,所经过的节点的顺序排列就称为“路径”
2、根:树顶端的节点称为根。一棵树只有一个根,如果要把一个节点和边的集合称为树,那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点
3、父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点
4、子节点:一个节点含有的子树的根节点称为该节点的子节点
5、兄弟节点:具有相同父节点的节点互称为兄弟节点
6、叶节点:没有子节点的节点称为叶节点,也叫叶子节点
7、子树:每个节点都可以作为子树的根,它和它所有的子节点、子节点的子节点等都包含在子树中
8、层:从根开始定义,根为第一层,根的子节点为第二层,以此类推
9、深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0
10、高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长
为什么使用二叉树?
树通常结合了有序数组和链表的优点,和有序数组查找的速度一样快,和链表插入和删除的速度一样
至于有序数组和链表的缺点,在之前学习ArrayList和LinkedList以及链表的时候,都有详细说明
可以参考:
Java集合(四)--基于JDK1.8的ArrayList源码解读
二叉树:
每个节点最多有两个子节点,也可以有一个子节点或者没有,这样的树称为二叉树,二叉树想对比较简单,而且常用。二叉树的两个子节点称为左子节点和右子节点
下面讲述的是二叉搜索树,定义:一个节点的左子节点的关键字值小于这个节点,右子节点的关键字值大于或等于父节点
Node类
public class Node {
private Object data; //节点数据
private Node leftChild; //左子节点
private Node rightChild; //右子节点
public void display() { //打印节点数据
}
}
Tree类
public class Tree {
private Node root;
public void find(Object key) {}
public void insert(Object key) {}
public void delete(Object key) {}
public void other(int key) {}
}
查找节点:
public Node find(int key) {
Node current = root; //从根节点开始
while (key != current.data) { //不断循环,直到找到和key相等的节点
if (key < current.data) { //如果key小于当前节点的数据,肯定就是就在左边
current = current.leftChild;
} else { //否则就在右边
current = current.rightChild;
}
if (current == null) { //如果current为null,证明已经到叶子节点,直接返回
return null;
}
}
return current;
}
插入节点:
public void insert(int data) {
Node newNode = new Node();
newNode.data = data;
if (root == null) {
root = newNode;
} else {
Node current = root;
Node parent;
while (true) {
parent = current; //保存父节点
if (data < current.data) {
current = current.leftChild;
if (current == null) { //如果左子节点为null,直接赋值
parent.leftChild = newNode;
return;
}
} else { //如果右子节点为null,直接赋值
current = current.rightChild;
if (current == null) {
parent.rightChild = newNode;
return;
}
}
}
}
}
遍历树:
遍历树就是以一定的顺序访问树的所有节点,相比插入、删除和搜索不是太常用,因为遍历的速度不快
遍历树的方式有三种:前序、中序、后序,其中中序是最常用的
前序遍历:根节点-->左子树-->右子树
中序遍历:左子树-->根节点-->右子树
后序遍历:左子树-->右子树-->根节点
public void prefixOrder(Node localRoot) {
if (localRoot != null) {
System.out.print(localRoot.data + " ");
prefixOrder(localRoot.leftChild);
prefixOrder(localRoot.rightChild);
}
}
public void infixOrder(Node localRoot) {
if (localRoot != null) {
infixOrder(localRoot.leftChild);
System.out.print(localRoot.data + " ");
infixOrder(localRoot.rightChild);
}
}
public void suffixOrder(Node localRoot) {
if (localRoot != null) {
suffixOrder(localRoot.leftChild);
suffixOrder(localRoot.rightChild);
System.out.print(localRoot.data + " ");
}
}
图例:
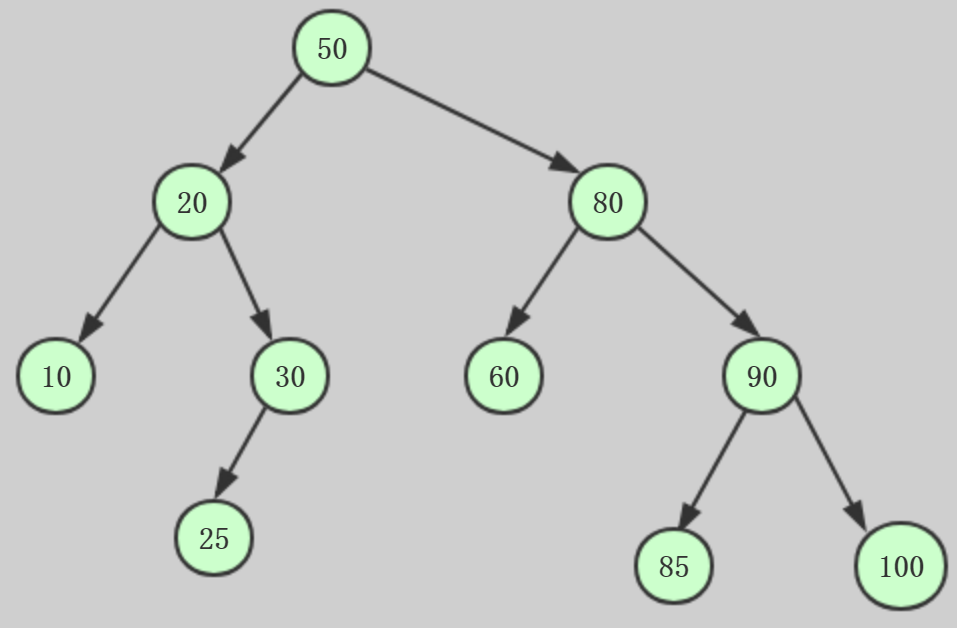
前序:50 20 10 30 25 80 60 90 85 100 中序:10 20 25 30 50 60 80 85 90 100 后序:10 25 30 20 60 85 100 90 80 50
查找最大值和最小值:
查找最大值和最小值对于二叉搜索树很简单的,最小值就是从根节点开始查询左子节点,不断递归,直到没有左子节点,就是最小值,而最大值就是递归调
用右子节点,如下图

public void findMin() {
Node current = root;
Node minNode = current;
while (current != null) {
minNode = current;
current = current.leftChild;
}
}
public void findMax() {
Node current = root;
Node minNode = current;
while (current != null) {
minNode = current;
current = current.rightChild;
}
}
删除节点:
删除节点是二叉搜索树中最复杂的操作,但是又非常重要。删除节点首先找到要删除的节点,有三种情况:
1、该节点是叶节点
2、该节点有一个子节点
3、该节点有两个子节点
第三种情况很复杂
删除没有子节点的节点:
要删除叶节点,只需要改变该节点的父节点的对应子字段的值,由指向该节点改为null就可以了。要删除的节点仍然存在,但它不是树的一部分了

public boolean deleteNoChild(int key) {
Node current = root;
Node parent = root;
boolean isLeftChild = true;
while (current.data != key) {
parent = current;
if (key < current.data) {
isLeftChild = true;
current = current.leftChild;
} else {
isLeftChild = false;
current = current.rightChild;
}
}
if (current == null) {
return false;
}
if (current.leftChild == null && current.rightChild == null) {
if (current == root) {
root = null;
} else if (isLeftChild) {
parent.leftChild = null;
} else {
parent.rightChild = null;
}
return true;
}
}
删除只有一个子节点的节点:
else if (current.rightChild == null) {
if (current == root) {
root = current.leftChild;
} else if (isLeftChild) {
parent.leftChild = current.leftChild;
} else {
parent.rightChild = current.rightChild;
}
} else if (current.leftChild == null) {
if (current == root) {
root = current.rightChild;
} else if (isLeftChild) {
parent.leftChild = current.rightChild;
} else {
parent.rightChild = current.rightChild;
}
}
把删除节点的子节点指向父节点就可以
删除有两个子节点的节点:
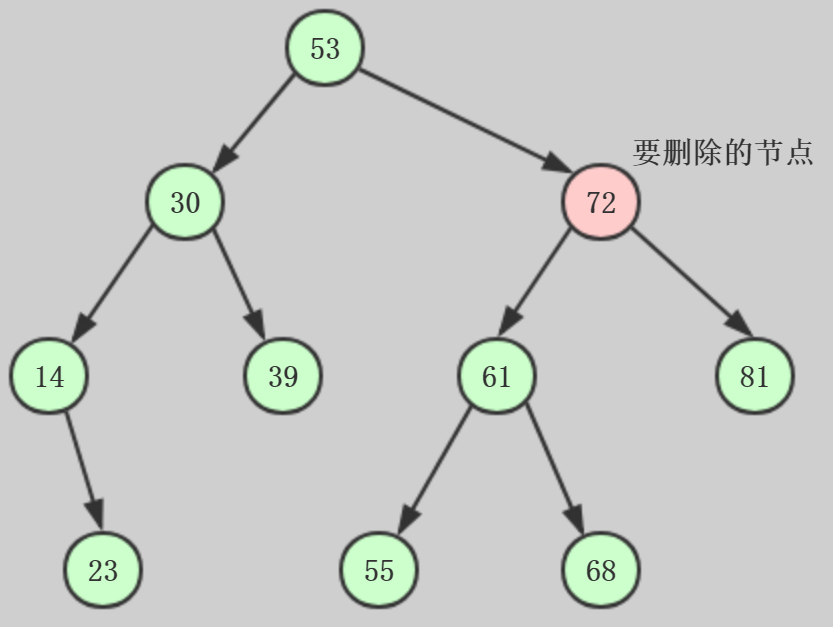
现在要删除节点72,那两个子节点61和81改如何放置,现在有个解决方法就是选取一个节点去替换被删除的节点,那该如何选取呢?
针对二叉搜索树而言,因为其节点按照关键字的值进行排序,所以寻找其后继节点去替换被删除节点,后继节点就是比被删除节点大的最小节点
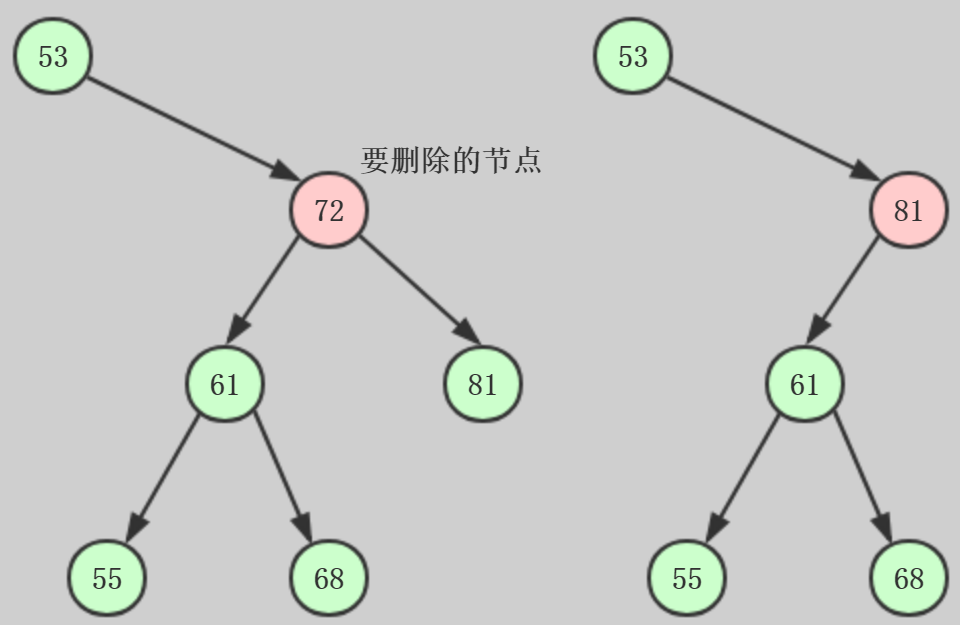
如何查找后继节点?
首先寻找要删除节点的右子节点(这里针对删除有两个子节点的节点的情况),然后寻找其左子节点,就有一个后继节点就是后继节点,如果该右节点没有左子
节点,该右节点就是后继节点,分别对应这两种情况
这里直接先给出代码示例:
else {
Node succuessor = getSuccessor(current);
if (current == root) { //当前节点为root,把后继节点赋值给root
root =succuessor;
} else if (isLeftChild) { //如果删除的节点为父节点的左子节点,后继节点赋值给父节点的leftChild
parent.leftChild = succuessor;
} else {
parent.rightChild = succuessor;
}
succuessor.leftChild = current.leftChild; //把current的左子节点指向后继节点的左子节点
return true;
}
//获取后继节点,默认删除节点有两个节点
private static Node getSuccessor(Node delNode) {
Node successorParent = delNode; //后继节点父节点
Node successor = delNode; //后继节点
Node current = delNode.rightChild; //当前节点从删除节点右节点开始
while (current != null) { //不断遍历当前节点的左子节点,直到找到最后一个
successorParent = successor;
successor = current;
current = current.leftChild;
}
//寻找后继节点结束
if (successor != delNode.rightChild) { //后继节点不是删除节点的右子节点,替换删除节点
successorParent.leftChild = successor.rightChild;
successor.rightChild = delNode.rightChild;
}
return successor;
}
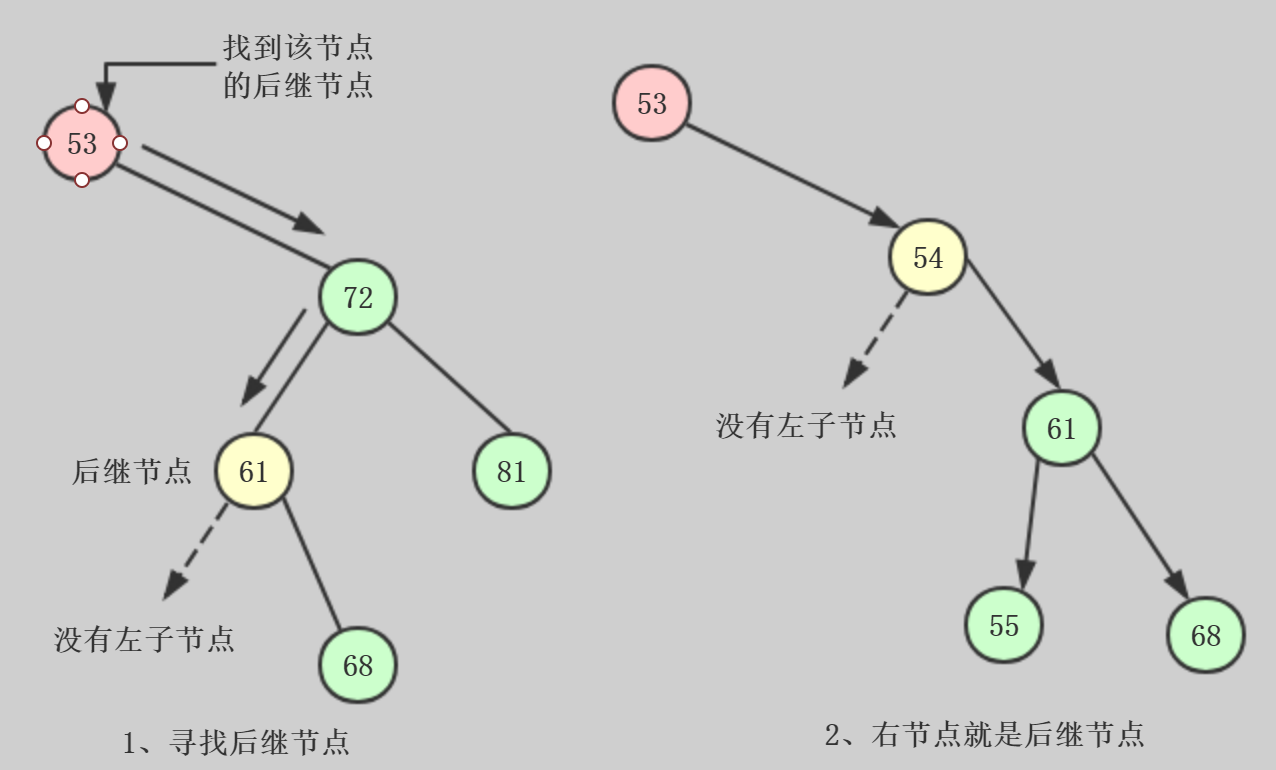
获取后继节点的代码是getSuccessor()前半部分,理解起来很简单
如果后继节点是删除节点的右子节点:
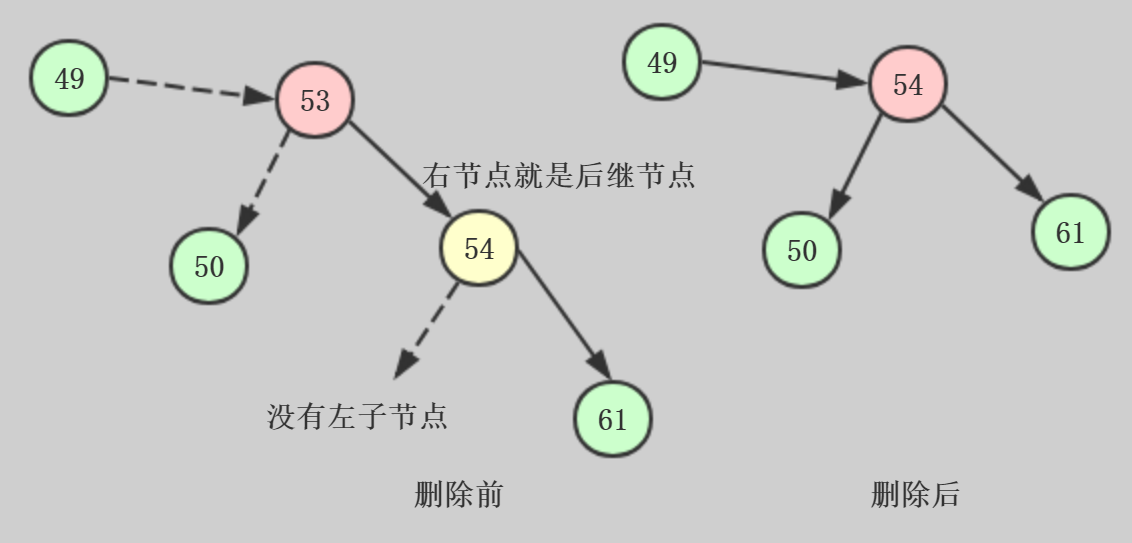
这时候只需要把后继节点为根的子树移到删除节点的位置
1、把current从它父节点的rightChild/leftChild字段删除,把这个字段指向后继节点
2、把current的左子节点移出来,把它插到后继节点的leftChild字段
具体代码在上面的delete()部分
如果后继节点是删除节点右子节点的左子节点:
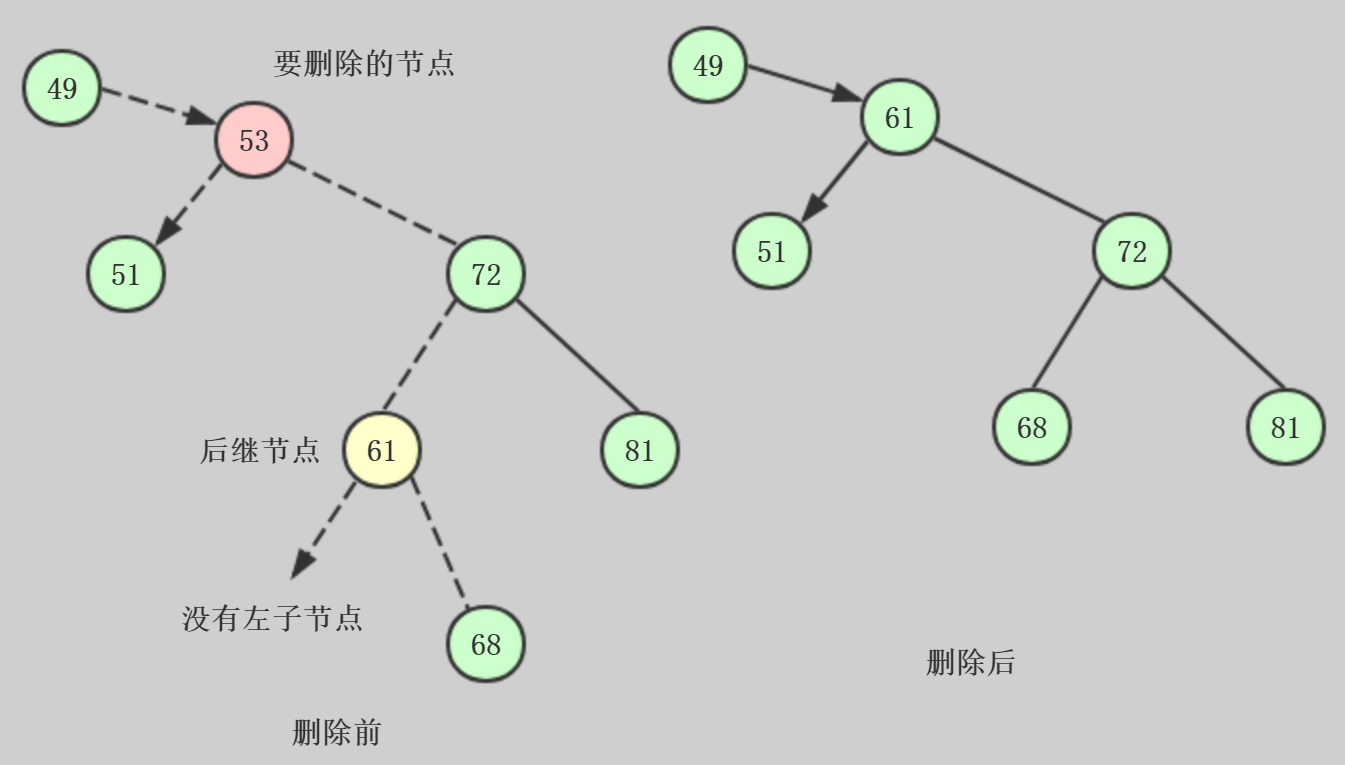
这里既然是后继节点了,肯定没有左子节点了,只有右子节点
操作步骤:
1、后继节点的父节点的左子节点设置为后继节点的右子节点,也就是把68设置到61的位置
2、把successor的rightChild字段设置为要delNode的右子节点
3、把current从它的父节点的rightChild删除,把这个字段设置为successor
4、把current的左子节点从current删除,successor的leftChild设置为current的左子节点
对应代码:
if (successor != delNode.rightChild) { //后继节点不是删除节点的右子节点,替换删除节点
1、 successorParent.leftChild = successor.rightChild;
2、 successor.rightChild = delNode.rightChild;
}
3、parent.rightChild = succuessor;
4、succuessor.leftChild = current.leftChild;
第一步:successor被它的右子树代替
第二步:delNode的右子节点移动到正确位置(当后继是delNode的右子节点这一步自动完成)
这两部的位置在getSuccessor()比delete()中好,因为可以在树中向下寻找后继节点的时候顺便找到后继节点的父节点
删除有必要吗?
上面删除的步骤真的很麻烦,一些人会在Node类中添加一个boolean类型的isDeleted,代表这个节点是否已经删除,查询的时候先判断标志。这样删除不会
改变树的结构
public class Node {
int data; //节点数据
Node leftChild; //左子节点
Node rightChild; //右子节点
private boolean isDeleted;
public void display() { //打印节点数据
}
}
二叉树的效率:
树的大部分操作都是从上到下一层层查找,那要花费多少时间?一个树有一半的节点在底层。一次有一半的都需要查找查找到底层
如果是满树,底层节点个数比其他节点数多1

这种情况和有序数组很相似,常见的树的操作时间复杂度为O(logN)
现在假如有1000000个数据
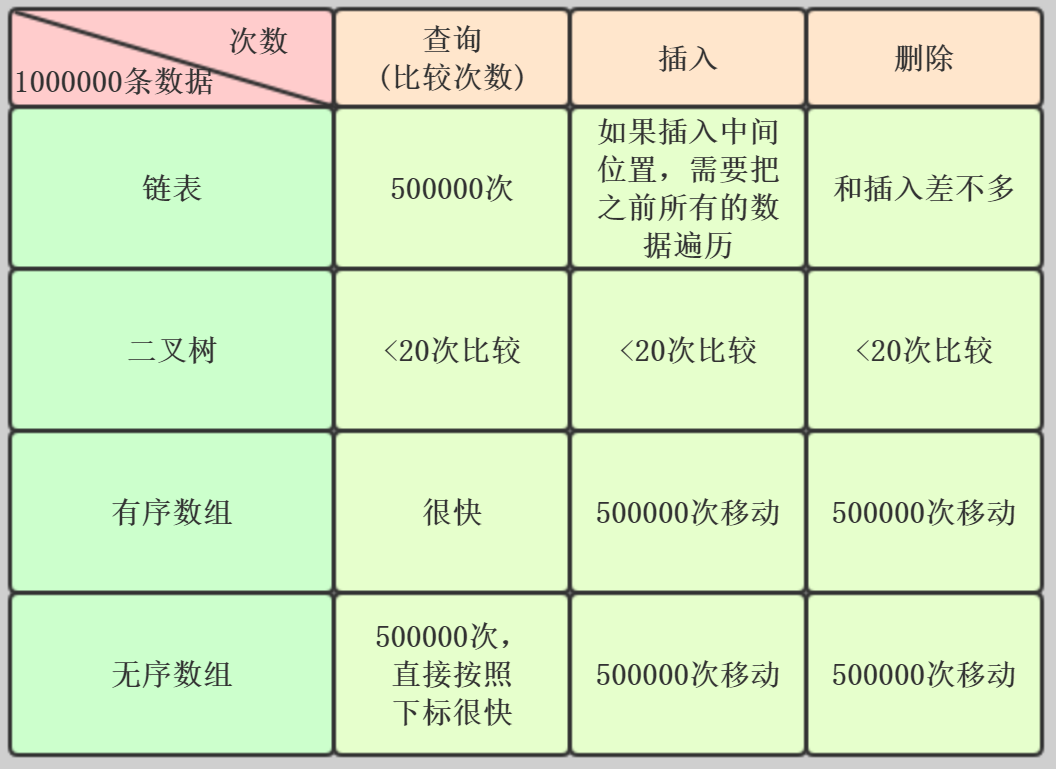
PS:以上都是平均值
所以,树对所有常用数据结构的操作都有很高的效率
遍历可能不如其他操作快,但是在大型数据库中,遍历是很少使用的操作,它更常用于程序中的辅助算法来解析算术或其它表达式
完整的Tree.java代码:
public class Tree {
Node root;
public Node find(int key) {
Node current = root;
while (key != current.data) {
if (key < current.data) {
current = current.leftChild;
} else {
current = current.rightChild;
}
if (current == null) {
return null;
}
}
return current;
}
public void insert(int data) {
Node newNode = new Node();
newNode.data = data;
if (root == null) {
root = newNode;
} else {
Node current = root;
Node parent;
while (true) {
parent = current;
if (data < current.data) {
current = current.leftChild;
if (current == null) {
parent.leftChild = newNode;
return;
}
} else {
current = current.rightChild;
if (current == null) {
parent.rightChild = newNode;
return;
}
}
}
}
}
public void prefixOrder(Node localRoot) {
if (localRoot != null) {
System.out.print(localRoot.data + " ");
prefixOrder(localRoot.leftChild);
prefixOrder(localRoot.rightChild);
}
}
public void infixOrder(Node localRoot) {
if (localRoot != null) {
infixOrder(localRoot.leftChild);
System.out.print(localRoot.data + " ");
infixOrder(localRoot.rightChild);
}
}
public void suffixOrder(Node localRoot) {
if (localRoot != null) {
suffixOrder(localRoot.leftChild);
suffixOrder(localRoot.rightChild);
System.out.print(localRoot.data + " ");
}
}
public Node findMin() {
Node current = root;
Node minNode = current;
while (current != null) {
minNode = current;
current = current.leftChild;
}
return minNode;
}
public Node findMax() {
Node current = root;
Node maxNode = current;
while (current != null) {
maxNode = current;
current = current.rightChild;
}
return maxNode;
}
public boolean delete(int key) {
Node current = root; //当前节点
Node parent = root; //当前节点的父节点
boolean isLeftChild = true; //被删除节点是否为父节点的左子节点,默认为左子节点
while (current.data != key) { //判断是否有和key相等的节点
parent = current;
if (key < current.data) { //如果小于当前节点值,肯定在左边
isLeftChild = true;
current = current.leftChild;
} else { //如果大于当前节点值,肯定在右边
isLeftChild = false;
current = current.rightChild;
}
}
if (current == null) { //如果没找到,直接返回false
return false;
}
if (current.leftChild == null && current.rightChild == null) { //删除的节点没有子节点
if (current == root) {
root = null;
} else if (isLeftChild) {
parent.leftChild = null;
} else {
parent.rightChild = null;
}
return true;
} else if (current.rightChild == null) { //删除的节点只有左节点
if (current == root) {
root = current.leftChild;
} else if (isLeftChild) { //如果被删除节点为父节点的左子节点,把delNode的右子节点赋值给父节点的左子节点
parent.leftChild = current.leftChild;
} else { //如果被删除节点为父节点的右子节点,把delNode的右子节点赋值给父节点的右子节点
parent.rightChild = current.rightChild;
}
return true;
} else if (current.leftChild == null) { //删除的节点只有右节点
if (current == root) {
root = current.rightChild;
} else if (isLeftChild) {
parent.leftChild = current.rightChild;
} else {
parent.rightChild = current.rightChild;
}
} else { //删除的节点右两个子节点
Node succuessor = getSuccessor(current); //获取后继节点
if (current == root) { //被删除节点为root,直接把后继节点赋值给root
root =succuessor;
} else if (isLeftChild) { //如果被删除节点为父节点的左子节点,父节点的左子节点指向后继节点
parent.leftChild = succuessor;
} else { //如果被删除节点为父节点的右子节点,父节点的右子节点指向后继节点
parent.rightChild = succuessor;
}
succuessor.leftChild = current.leftChild; //把被删除节点的左子节点指向后继节点的左子节点
return true;
}
return false;
}
//获取后继节点,默认删除节点有两个节点
private static Node getSuccessor(Node delNode) {
Node successorParent = delNode; //后继节点父节点
Node successor = delNode; //后继节点
Node current = delNode.rightChild; //当前节点从删除节点右节点开始
while (current != null) { //不断遍历当前节点的左子节点,直到找到最后一个,就是后继节点
successorParent = successor;
successor = current;
current = current.leftChild;
}
if (successor != delNode.rightChild) { //后继节点不是删除节点的右子节点,也就是为右子节点的左子节点,或者后序左节点,然后替换删除节点
successorParent.leftChild = successor.rightChild;
successor.rightChild = delNode.rightChild;
}
return successor;
}
public void other(int key) {}
}
测试代码:
public static void main(String[] args) {
Tree tree = new Tree();
tree.insert(50);
tree.insert(20);
tree.insert(80);
tree.insert(10);
tree.insert(30);
tree.insert(60);
tree.insert(90);
tree.insert(25);
tree.insert(85);
tree.insert(100);
tree.prefixOrder(tree.root);
System.out.println("");
tree.infixOrder(tree.root);
System.out.println("");
tree.suffixOrder(tree.root);
System.out.println("");
tree.delete(10);//删除没有子节点的节点
tree.delete(30);//删除有一个子节点的节点
tree.delete(80);//删除有两个子节点的节点
System.out.println(tree.findMax().data);
System.out.println(tree.findMin().data);
System.out.println(tree.find(50));
System.out.println(tree.find(200));
}
输出结果: 50 20 10 30 25 80 60 90 85 100 10 20 25 30 50 60 80 85 90 100 10 25 30 20 60 85 100 90 80 50 100 20 com.it.tree.Node@65b54208 null
PS:删除的步骤和三种遍历方式,想对难理解一点,可以对照图,一步步查看完整版Tree.java代码,最终肯定可以理解的
内容参考:<Java数据结构和算法>