汉诺塔
设(T_n)为(n)个圆盘的方案数,显然(T_0=0,T_1=1)
构造一种方案:将(n-1)个圆盘移动到第二根柱子上,将最大的圆盘移动到第三根柱子,再将(n-1)个圆盘移动过去
那么按照此方案至少有
[T_n≤2T_{n-1}+1,n>0
]
且易证最优
[T_n≥2T_{n-1}+1,n>0
]
所以
[T_0=0,T_n=2T_{n-1}+1,n>0
]
(n)很大时递归式不好算,考虑一个封闭形式
观察好像有
[T_n=2^n-1
]
至少(T_1=2^1-1)
那么当(T_{n-1}=2^{n-1}-1)时,有(T_n=2T_{n-1}+1=2^n-1),根据归纳得(T_n=2^n-1)
有时我们观察不到(T_n=2^n-1)
也许更容易发现(U_n=T_n+1=2^n)
平面上的直线
求平面上(n)条直线所界定的区域的最大个数(L_n)
显然(L_0=1,L_1=2,L_2=4)
那么似乎有(L_n=2^n)
然后有(L_3=7),What a pity
第(n)条直线使得区域增加(k)个,当且仅当对(k)个已有区域进行分割,即与已有直线有(k-1)个交点,此前仅有(n-1)条直线
[L_n≤L_{n-1}+n,n>0
]
易证等号可取(第(n)条与此前所有直线有交点可取)
[L_0=1,L_n=L_{n-1}+n,n>0
]
展开(L_n)得
[L_n=L_0+1+2+3+…+n
]
[L_n=1+S_n
]
[S_n=1+2+3+…+n
]
(S_n)又称三角形数,是一个有(n)行的三角形阵列中保龄球的个数
高斯九岁得出了计算(S_n)的办法
[S_n=1+2+3+…+n
]
[S_n=n+(n-1)+(n-2)+…+1
]
[2S_n=(n+1)+(n+1)+…+(n+1)=n*(n+1)
]
[S_n=frac{n*(n+1)}{2}
]
由此得出
[L_n=1+frac{n*(n+1)}{2},n≥0
]
归纳也可得
[L_n=L_{n-1}+n=(frac{(n-1)*n}{2}+1)+n=1+frac{n*(n+1)}{2}
]
问题变形:用折线代替直线,每个折线包含一个尖,求(n)条折线能界定的区域最大个数(Z_n)
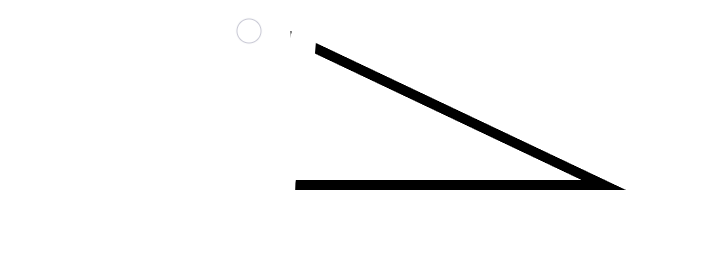
先列小数据:(Z_0=1,Z_1=2,Z_2=7)
观察发现(根本没法发现x):一个折线相当于两条相交直线去掉一半(去掉蓝色一半)
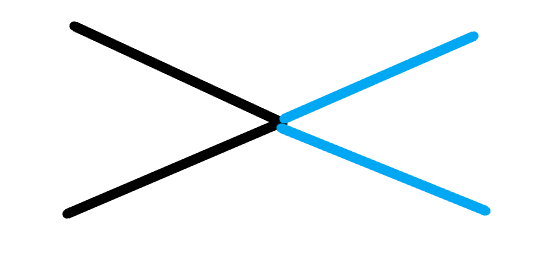
等价于:每条折线我们失去了两条直线界定空间中的两个,也就是
[Z_n=L_{2n}-2n
]
[Z_n=2n^2-n+1,n≥0
]
约瑟夫问题
(n)个人围成一个圆圈,隔一个杀一个,直到只有一人存活,求存活的人的编号
如(n=10)时,杀死的顺序是(2、4、6、8、10、3、7、1、9)
于是得到(J(10)=5)
猜测(J(n)=frac{n}{2})
然后试了几次就(GG)了
假设有(2n)个人,经过第一轮只剩下奇数编号的人,那么(3)号就成为下一个要离开的人
也就是除了每个人的号码加倍再减一,其他规则同(n)个人一致
那么(J(2n)=2J(n)-1)
由此(J(20)=2*J(10)-1,n≥1)
同理(J(2n+1)=2J(n)+1)
结合得到递推式
[J(1)=1
]
[J(2n)=2J(n)-1,n≥1
]
[J(2n+1)=2J(n)+1,n≥1
]
指数级的递推式更快捷
打表
[J(1)=1
]
[J(2)=1,J(3)=3
]
[J(4)=1,J(5)=3,J(6)=5,J(7)=7
]
[J(8)=1,J(9)=3,J(10)=5,J(11)=7,J(12)=9,J(13)=11,J(14)=13,J(15)=15
]
[J(16)=1
]
似乎可以按(2)的幂分组,并且每组开始(J(n)=1)
[J(2^m+l)=2l+1,m≥0,0≤l<2^m
]
对(m)归纳
[J(1)=1,J(2^m+l)=2J(2^{m-1}+frac{l}{2})-1=2(frac{l}{2}+1)-1=2l+1
]
观察前式可知
[J(2n+1)-J(2n)=2
]
拓展:
假设(n)的二进制展开式是
[n=(b_mb_{m-1}…b_1b_0)_2
]
等价于
[n=b_m*2^m+b_{m-1}*2^{m-1}+…+b_1*2+b_0
]
其中(b_i=0)或(1),而首位(b_m=1)
那么依次有
[n=(1b_{m-1}…b_1b_0)_2
]
[l=(0b_{m-1}…b_1b_0)_2
]
[2l=(b_{m-1}…b_1b_00)_2
]
[2l+1=(b_{m-1}…b_1b_01)_2
]
[J(n)=2l+1,J(n)=(b_{m-1}…b_1b_0b_m)_2
]
最后得到了
[J((b_mb_{m-1}…b_1b_0)_2)=(b_{m-1}…b_1b_0b_m)_2
]
(n)向左循环一位就得到了(J(n))
如果一直用二进制表示也许很快就能发现
根据循环可以期待进行(m+1)次迭代再次得到(n)
但事实上例如(J((1101)_2)=(1011)_2),再迭代一次(J((1011)_2)=(111)_2),当(0)为首位时会消失
实际上(J(n))必然(≤n),于是如果(J(n)<n)就不可能迭代回(n)
反复迭代得到一系列递减数列后最终会到达一个不动点(J(n)=n)(至少还有(J(1)=1)呢)
显然这个不动点的二进制表示中全是(1)
所以不动点的数值是(2^{v(n)}-1),其中(v(n))是(n)的二进制表示中(1)的个数
回去考虑第一个猜测:(J(n)=frac{n}{2})
考虑它什么时候成立
[J(n)=frac{n}{2}
]
[2l+1=frac{2^m+l}{2}
]
[l=frac{2^m-2}{3}
]
当(l=frac{2^m-2}{3})为整数时,(n=2^m+l)就是一个解
不难验证,当(m)为奇数时,(2^m-2)是(3)的倍数,但当(m)为偶数时则不然(后面再研究)
前几个解:
[m=1,l=0,n=2,J(n)=1,n=(10)_2
]
[m=3,l=2,n=10,J(n)=5,n=(1010)_2
]
[m=5,l=10,n=42,J(n)=21,n=(101010)_2
]
[m=7,l=42,n=170,J(n)=85,n=(10101010)_2
]
其中通过二进制很好看出来
再拓展:
引入
[f(1)=α,f(2n)=2f(n)+β,f(2n+1)=2f(n)+γ
]
打表
[f(1)=α
]
[f(2)=2α+β,f(3)=2α+γ
]
[f(4)=4α+3β,f(5)=4α+2β+γ,f(6)=4α+β+2γ,f(7)=4α+3γ
]
[f(8)=8α+7β,f(9)=8α+6β+γ
]
一般地
[f(n)=A(n)α+B(n)β+C(n)γ
]
[A(n)=2^m,B(n)=2^m-l-1,C(n)=l
]
归纳法易证,但是很难直接得出此结论
下面考虑一般方法
令(f(n)=A(n)),可得(α=1,β=γ=0)
[A(n)=1,A(2n)=2A(n),A(2n+1)=2A(n)
]
成立
若代入(f(n)=1)
[1=α,1=2*1+β,1=2*1+γ
]
此时(α=1,β=γ=-1)
类似,若代入(f(n)=n),得到(α=1,β=0,γ=1)
但由此我们有
[A(n)=2^m,A(n)-B(n)-C(n)=1,A(n)+C(n)=n
]
[C(n)=n-A(n)=l
]
[B(n)=A(n)-1-C(n)=2^m-1-l
]
猜想的结果被完美推出
此为成套方法,有多少个独立参数就需多少独立特解
将成套方法用于约瑟夫问题:
已知
[J((b_mb_{m-1}…b_1b_0)_2)=(b_{m-1}…b_1b_0b_m)_2
]
若令(β_0=β,β_1=γ)
[f(1)=α
]
[f(2n+j)=2f(n)+β_j,j=0,1,n≥1
]
按二进制展开就是
[f((b_mb_{m-1}…b_1b_0)_2)=2f((b_mb_{m-1}…b_1)_2)+β_{b_0}
]
[=4f((b_mb_{m-1}…b_2)_2)+2β_{b_1}+β_{b_0}
]
[=2^mα+2^{m-1}β_{b_{m-1}}+…+2β_{b_1}+β_{b_0}
]
则有
[f((b_mb_{m-1}…b_1b_0)_2)=(αb_{m-1}…b_1b_0)_2
]
打表
[f(1)=α
]
[f(2)=2α+β,f(3)=2α+γ
]
[f(4)=4α+2β+β,f(5)=4α+2β+γ,f(6)=4α+β+2γ,f(7)=4α+γ+2γ
]
例如
[n=100=(1100100)_2,α=1,β=-1,γ=1
]
[f(n)=64+32-16-8+4-2-1=73
]
以(100)为例,(1100100)中每个(1)被(0)((-1))减至最靠右的(0)的位置上
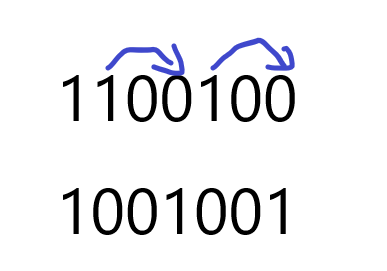
由此推出循环移位性质
更拓展:
[f(j)=α_j,1≤j<d
]
[f(dn+j)=cf(n)+β_j,0≤j<d,n>0
]
则有
[f((b_mb_{m-1}…b_1b_0)_d)=(αb_{m-1}…b_1b_0)_c
]
例如假设
[f(1)=34,f(2)=5,f(3n)=10f(n)+76,n>0,f(3n+1)=10f(n)-2,n>0,f(3n+2)=10f(n)+8,n>0
]
有(d=3,c=10),要求(d=19)
则
[f(19)=f((201)_3)=(5,76,-2)_{10}=5*100+76*10-2=1258
]
约瑟夫问题有趣起来了
习题
1.当(n=2)时,(1)到(n-1)与(2)到(n)不存在交叉部分,不具有传递性
[T_0=0,T_1=2
]
[T_n=3T_{n-1}+2
]
[T_n=3^n-1
]
3.显然
4.数学归纳法
(n=1)时,移动次数为(0)或(1)
(g(1)=1=2^n-1)
对于第(n)个盘子,若在第三根柱子上(g(n)=g(n-1)≤2^{n-1}-1)
若不在第三根柱子上(g(n)=g(n-1)+1+T_{n-1}≤2^n-1)
5.不能,第四个圆与前三个圆最多有6个交点,最多增加6个表示集合
6.(f(1)=f(2)=0,f(n)=f(n-1)+n-2=S_{n-2},n>2)
7.(H(1)=J(2)-J(1)=0)
[Q_2=frac{1+β}{α}
]
[Q_3=frac{1+frac{1+β}{α}}{β}=frac{1+α+β}{αβ}
]
[Q_4=frac{1+frac{1+α+β}{αβ}}{frac{1+β}{α}}=frac{α+frac{1+α+β}{β}}{1+β}=frac{1+α+frac{1+α}{β}}{1+β}=frac{frac{(1+α)(1+β)}{β}}{1+β}=frac{1+α}{β}
]
[Q_5=frac{1+frac{1+α}{β}}{frac{1+α+β}{αβ}}=frac{αβ+α(1+α)}{1+α+β}=frac{α(1+α+β)}{1+α+β}=α
]
a:
[(frac{x_1+…+x_n}{n})^n≥x_1…x_n
]
[(frac{x_1+…+x_{n-1}+frac{x_1+…x_{n-1}}{n-1}}{n})^n≥x_1…x_{n-1}*frac{x_1+…+x_{n-1}}{n-1}
]
[(frac{x_1+…+x_{n-1}}{n-1})^n≥x_1…x_{n-1}*frac{x_1+…+x_{n-1}}{n-1}
]
[(frac{x_1+…+x_{n-1}}{n-1})^{n-1}≥x_1…x_{n-1}
]
b:
引理一:基本不等式:
[ab≤(frac{a+b}{2})^2
]
证明:
[(frac{sum_{i=1}^{n}x_i}{n})^n≥prod_{i=1}^{n}x_i
]
[(frac{sum_{i=n+1}^{2n}x_i}{n})^n≥prod_{i=n+1}^{2n}x_i
]
两式相乘
[(frac{sum_{i=1}^{n}x_i}{n}*frac{sum_{i=n+1}^{2n}x_i}{n})^n≥prod_{i=1}^{2n}x_i
]
由引理一得
[(frac{sum_{i=1}^{2n}x_i}{2n})^{2n}≥prod_{i=1}^{2n}x_i
]
c.
疑问,对于a.的证明,题目给出了特定条件,是否对一般地情况成立
引用
补充对不等式的证明:
引理一:
[x≤e^{x-1}
]
证明:
如果存在(x_i=0),那么显然成立
若任意(x_i>0),令
[a=frac{sum_{i=1}^{n}x_i}{n}>0
]
对任意(x_i)有
[frac{x_i}{a}≤e^{frac{x_i}{a}-1}
]
所有式子相乘得到
[frac{prod_{i=1}^{n}x_i}{a^n}≤e^{sum_{i=1}^{n}frac{x_i}{a}-n}=e^{n-n}=1
]
[a^n≥prod_{i=1}^{n}x_i
]
[(frac{sum_{i=1}^{n}x_i}{n})^n≥prod_{i=1}^{n}x_i
]
(Q_n):先将(n-1)个盘子挪到(C),将第(n)个盘子挪到(B),再将(n-1)个盘子挪到(B)
(Q_n=R_{n-1}+1+R_{n-1}=2R_{n-1}+1)
(R_n):将(n-1)个盘子挪到(A),将第(n)个盘子挪到(C),将(n-1)个盘子挪到(B),将第(n)个盘子挪到(A),将(n-1)个盘子挪到(A)
(R_n=R_{n-1}+1+Q_{n-1}+1+R_{n-1}=Q_n+Q_{n-1}+1)
a.
[P_n=2P_{n-1}+2=2^{n+1}-2
]
b.
注意,只需要在最后恢复,经偶数次(a)中放置即可恢复顺序
[Q_n=4P_{n-1}+3=4*(2^n-2)+3=2^{n+2}-5
]
[P_n=2P_{n-1}+m_n=sum_{i=1}^{n}2^{n-i}m_i
]
每条(Z)比三条直线少了(5)块区域
[F_n=L_{3n}-5n=frac{3n(3n+1)}{2}-5n+1=frac{9n^2-7n+2}{2}
]
或,第(n)个折线与前(n-1)条折线每条最多有(9)个交点,共计最多(9n-9)个交点,可新增(9n-8)个区域
(F_n=F_{n-1}+9n-8=frac{9n^2-7n+2}{2})$
新切一刀增加的空间数量为切面上直线划分的二维平面数量
[P_n=P_{n-1}+L_{n-1}
]
类似的,设(X_n)是一条直线上(n)个点所确定的一维区域的最大个数,有
[L_n=L_{n-1}+X_{n-1}
]
更有趣的:
[X_n=dbinom{n}{0}+dbinom{n}{1}
]
[L_n=dbinom{n}{0}+dbinom{n}{1}+dbinom{n}{2}
]
[P_n=dbinom{n}{0}+dbinom{n}{1}+dbinom{n}{2}+dbinom{n}{3}
]
符合上述规律:
[P_n=P_{n-1}+L_{n-1}=dbinom{n-1}{0}+dbinom{n-1}{1}+dbinom{n-1}{2}+dbinom{n-1}{3}+dbinom{n-1}{0}+dbinom{n-1}{1}+dbinom{n-1}{2}
]
[=dbinom{n-1}{0}+(dbinom{n-1}{0}+dbinom{n-1}{1})+(dbinom{n-1}{1}+dbinom{n-1}{2})+(dbinom{n-1}{2}+dbinom{n-1}{3})
]
[=dbinom{n}{0}+dbinom{n}{1}+dbinom{n}{2}+dbinom{n}{3}
]
组合意义待探究
(I(2)=2,I(3)=1)
若(n)为偶数,第一轮删掉(2,4,6,…),剩下(1,3,5,……),再从(1)开始,那么(I(n)=2I(frac{n}{2})-1)
若(n)为奇数,第一轮过后再从(3)开始,那么(I(n)=2I(frac{n}{2})+1)


