上一篇文章写了栈的相关知识,而本文会讲一下队列
队列是一种特殊的线性表,在尾部插入(入队Enqueue),从头部删除(出队Dequeue),和栈的特性相反,存取数据特点是:FIFO
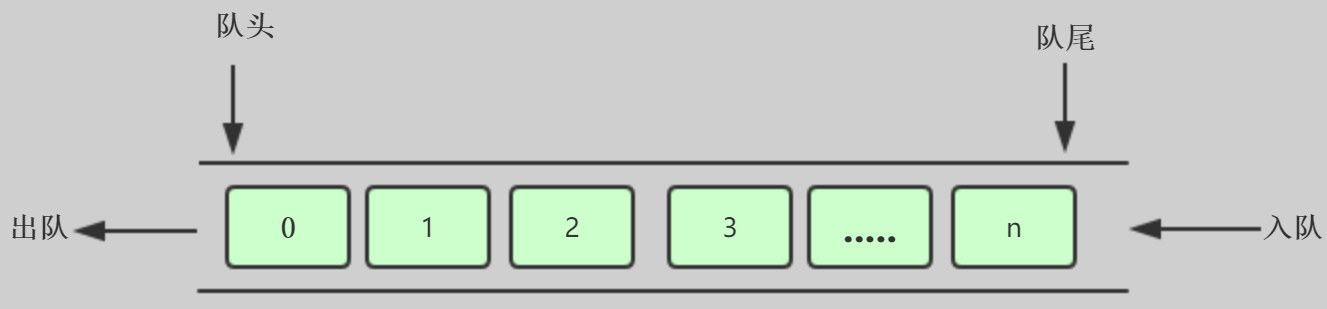
Java中queue源码:
public interface Queue<E> extends Collection<E> {
boolean add(E e); //添加一条数据到队尾,成功返回true,否则false
boolean offer(E e); //添加一条数据到队尾,如果队列满了,会返回null
E remove(); //从队头删除一条数据,如果是空队列,会发生异常
E poll(); //从队头删除一条数据,如果是空队列,会返回null
E element(); //返回队头的数据,如果是空队列,会发生异常
E peek(); //返回队头的数据,如果是空队列,会返回null
}
queue直接继承Collection,有6个基本方法实现增删查的功能
单向队列:
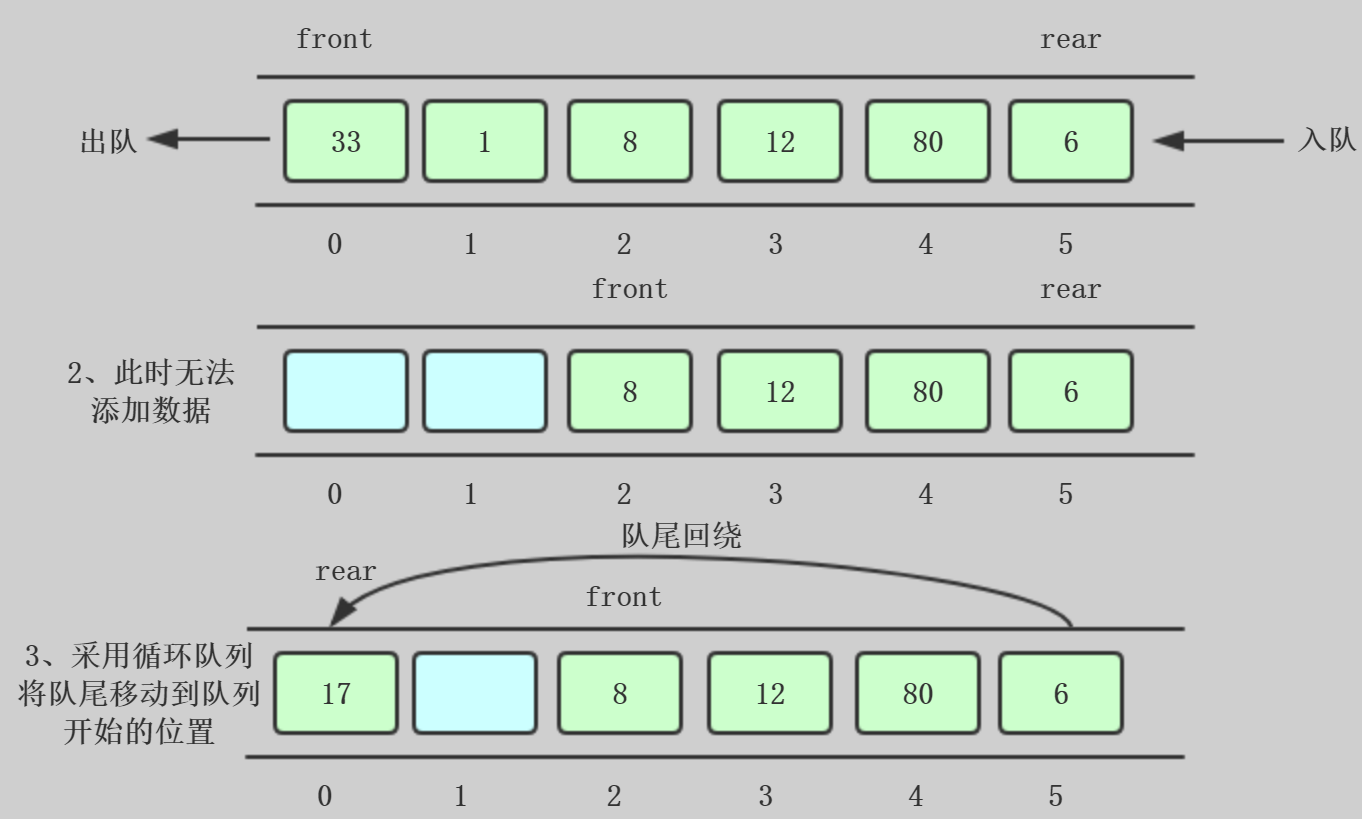
PS:删除的数据还是保存在内存中的,只是不能被访问,因为front位置移动了
上图中第二步,我们从队头front删除一些数据,然后队尾由于插入数据,rear移动到最后,此时无法插入数据
为了避免队列不满但是不能插入数据的情况,采用第三步:循环队列,将队尾回绕到队列开始的位置
Java代码实现单向队列:
public class MyQueue<E> {
private int maxSize; //队列总大小
private Object[] elementData; //保存数据的数组
private int front; //队头
private int rear; //队尾
private int nItems; //队列元素的数量
public MyQueue(int value) {
maxSize = value;
elementData = new Object[value];
front = 0;
rear = -1;
nItems = 0;
}
public void add(E e) {
if (isFull()) {
System.out.println("当前队列已满");
} else {
if (rear == maxSize - 1) { //如果rear已经指向最后面,将队尾回绕到队列开始的位置
rear = -1;
}
elementData[++rear] = e; //rear后移一位(首位为0),并且插入数据
nItems++; //元素数量+1
}
}
//移除数据
public E remove(){
E temp = null;
if (isEmpty()) {
System.out.println("当前为空队列,无法删除");
} else {
temp = (E)elementData[front++]; //返回队头front的数据,然后front后移一位
if (front == maxSize) { //如果front已经后移到最末尾了,front重置
front = 0;
}
nItems--; //元素数量-1
}
return temp;
}
public E peek(){ //查看队头数据
return (E)elementData[front];
}
public boolean isFull(){
return (nItems == maxSize);
}
public boolean isEmpty(){
return (nItems ==0);
}
public int getSize(){ //返回队列的大小
return nItems;
}
}
public static void main(String[] args) {
MyQueue<Integer> queue = new MyQueue<>(5);
int i = 0;
while (!queue.isFull()) {
queue.add(i++);
}
queue.add(6); //当前队列已满,无法添加了
while (!queue.isEmpty()) {
queue.remove();
}
}
输出结果:当前队列已满
优先级队列:
优先级队列是比栈和队列更专用的数据结构,一般情况下,和浦东队列一样,优先级队列有一个头部和一个尾部,也是从头部移除数据。
不过优先级队列中,元素按照关键字是有序的。关键字最小的元素总是在头部,元素在插入的时候按照顺序插入到合适的位置以确保队列的顺序
优先级队列在程序中也有很多应用,例如:图的最小生成树
这里我们使用简单数组实现优先级队列,这种方式比较慢,但是很简单。优先级队列一般都是通过队来实现,在后面会降到
代码实现:
public class MyPriorityQueue {
private int maxSize; //队列总大小
private Object[] elementData; //保存数据的数组
private int nItems; //队列元素的数量
public MyPriorityQueue(int value) {
maxSize = value;
elementData = new Object[value];
nItems = 0;
}
public boolean add(int e) { //添加元素,关键字小的元素在头部,通过插入排序实现
int j;
if (nItems == 0) {
elementData[nItems++] = e;
} else {
j = nItems - 1;
while (j >= 0 && e > (int)elementData[j]) {
elementData[j+1] = elementData[j];
j--;
}
elementData[j+1] = e;
nItems++;
}
return true;
}
//移除数据
public Object remove(){ //删除一条数据,返回老数据
Object value = elementData[nItems-1];
elementData[nItems-1] = null;
nItems--;
return value;
}
public Object peekMin() { //返回优先级最高的元素
return elementData[nItems-1];
}
//判断是否为空
public boolean isEmpty(){
return (nItems == 0);
}
//判断是否满了
public boolean isFull(){
return (nItems == maxSize);
}
}
public static void main(String[] args) {
MyPriorityQueue queue = new MyPriorityQueue(5);
int i = 0;
while (!queue.isFull()) {
queue.add(i++);
}
while (!queue.isEmpty()) {
System.out.println(queue.peekMin());;
queue.remove();
}
}
打印结果: 0 1 2 3 4
add()通过插入排序实现,时间复杂度O(N),如果忘记插入排序,可以参考:Java数据结构和算法(三)--三大排序--冒泡、选择、插入排序
PS:Queue一般作为程序的某种实现,而不是用来保存数据
内容参考:<Java数据结构和算法>