Color a Tree
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 7861 | Accepted: 2692 |
Description
Bob is very interested in the data structure of a tree. A tree is a directed graph in which a special node is singled out, called the "root" of the tree, and there is a unique path from the root to each of the other nodes.
Bob intends to color all the nodes of a tree with a pen. A tree has N nodes, these nodes are numbered 1, 2, ..., N. Suppose coloring a node takes 1 unit of time, and after finishing coloring one node, he is allowed to color another. Additionally, he is allowed to color a node only when its father node has been colored. Obviously, Bob is only allowed to color the root in the first try.
Each node has a "coloring cost factor", Ci. The coloring cost of each node depends both on Ci and the time at which Bob finishes the coloring of this node. At the beginning, the time is set to 0. If the finishing time of coloring node i is Fi, then the coloring cost of node i is Ci * Fi.
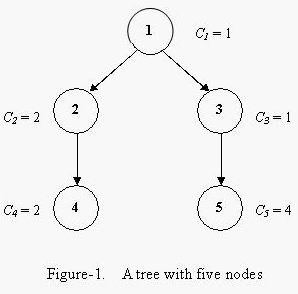
For example, a tree with five nodes is shown in Figure-1. The coloring cost factors of each node are 1, 2, 1, 2 and 4. Bob can color the tree in the order 1, 3, 5, 2, 4, with the minimum total coloring cost of 33.
Given a tree and the coloring cost factor of each node, please help Bob to find the minimum possible total coloring cost for coloring all the nodes.
Bob intends to color all the nodes of a tree with a pen. A tree has N nodes, these nodes are numbered 1, 2, ..., N. Suppose coloring a node takes 1 unit of time, and after finishing coloring one node, he is allowed to color another. Additionally, he is allowed to color a node only when its father node has been colored. Obviously, Bob is only allowed to color the root in the first try.
Each node has a "coloring cost factor", Ci. The coloring cost of each node depends both on Ci and the time at which Bob finishes the coloring of this node. At the beginning, the time is set to 0. If the finishing time of coloring node i is Fi, then the coloring cost of node i is Ci * Fi.
For example, a tree with five nodes is shown in Figure-1. The coloring cost factors of each node are 1, 2, 1, 2 and 4. Bob can color the tree in the order 1, 3, 5, 2, 4, with the minimum total coloring cost of 33.

Given a tree and the coloring cost factor of each node, please help Bob to find the minimum possible total coloring cost for coloring all the nodes.
Input
The input consists of several test cases. The first line of each case contains two integers N and R (1 <= N <= 1000, 1 <= R <= N), where N is the number of nodes in the tree and R is the node number of the root node. The second line contains N integers, the i-th of which is Ci (1 <= Ci <= 500), the coloring cost factor of node i. Each of the next N-1 lines contains two space-separated node numbers V1 and V2, which are the endpoints of an edge in the tree, denoting that V1 is the father node of V2. No edge will be listed twice, and all edges will be listed.
A test case of N = 0 and R = 0 indicates the end of input, and should not be processed.
A test case of N = 0 and R = 0 indicates the end of input, and should not be processed.
Output
For each test case, output a line containing the minimum total coloring cost required for Bob to color all the nodes.
Sample Input
5 1 1 2 1 2 4 1 2 1 3 2 4 3 5 0 0
Sample Output
33
Source
【题解】
这个贪心题是真难呐,看了很多一知半解的题解,想了好久才想明白。
这里有一个非常好的、网上为数不多的正确的证明,仅供参考

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cstdlib> 5 const int INF = 0x3f3f3f3f; 6 const int MAXN = 1000 + 10; 7 inline void read(int &x) 8 { 9 x = 0;char ch = getchar(), c = ch; 10 while(ch < '0' || ch > '9')c = ch, ch = getchar(); 11 while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar(); 12 if(c == '-')x = -x; 13 } 14 int f[MAXN], fa[MAXN], ans, n, root, value[MAXN], b[MAXN], size[MAXN]; 15 inline void init() 16 { 17 memset(b, 0, sizeof(b)); 18 for(register int i = 1;i <= n;++ i) size[i] = 1, f[i] = i; 19 f[root] = root; 20 b[root] = 1; 21 } 22 int find(int x) 23 { 24 return f[x] == x ? x : f[x] = find(f[x]); 25 } 26 int main() 27 { 28 register int tmp,tmp1,tmp2,v; 29 register double ma; 30 while(scanf("%d %d", &n, &root) && (n + root)) 31 { 32 ans = 0; 33 init(); 34 for(register int i = 1;i <= n;++ i) read(value[i]); 35 for(register int i = 1;i < n;++ i) read(tmp1), read(tmp2),fa[tmp2] = tmp1; 36 //n - 1轮缩点操作 37 for(register int i = 1;i < n;++ i) 38 { 39 ma = -1; 40 for(register int j = 1;j <= n;++ j) 41 if(!b[j] && ma < (double)value[j]/size[j] && find(j) != root) 42 ma = (double)value[j]/size[j], v = j; 43 b[v] = 1; 44 tmp = find(fa[v]); 45 f[v] = tmp; 46 ans += value[v] * size[tmp]; 47 value[tmp] += value[v]; 48 size[tmp] += size[v]; 49 } 50 ans += value[root]; 51 printf("%d ", ans); 52 } 53 return 0; 54 }
