昨天老大说让我写一个判断鼠标从什么方向进入容器的js插件。第一反应就是算出进入容器的点的坐标,然后与四个边线的位置比较。可是又觉得这样的想法好老土,没有一点技巧性。
在网上搜索发现有一个很多人都转载的算法,如下:
1 $("#wrap").bind("mouseenter mouseleave",function(e) { 2 var w = $(this).width(); 3 var h = $(this).height(); 4 var x = (e.pageX - this.offsetLeft - (w / 2)) * (w > h ? (h / w) : 1); 5 var y = (e.pageY - this.offsetTop - (h / 2)) * (h > w ? (w / h) : 1); 6 var direction = Math.round((((Math.atan2(y, x) * (180 / Math.PI)) + 180) / 90) + 3) % 4; //direction的值为“0,1,2,3”分别对应着“上,右,下,左” 7 var eventType = e.type; 8 var dirName = new Array('上方','右侧','下方','左侧'); 9 if(e.type == 'mouseenter'){ 10 $("#result").html(dirName[direction]+'进入'); 11 }else{ 12 $('#result').html(dirName[direction]+'离开'); 13 } 14 });
就这么几行代码,将我印象里会有一长串的if else或者switch来完成的事完美的解决掉。在感到神奇之后,更多的是不解,因为看不懂。在网上搜索一番,也没有找到有谁来分析这个算法。于是自己研究了一下,现在写下来,作为自己的一份学习笔记,也希望能够和大家分享。
有不对的地方,或者有更好的理解,请告诉我,谢谢!
原理:以div容器的中心点作为圆心,以高和宽的最小值作为直径画圆,将圆以[π/4,3π/4),[3π/4,5π/4),[5π/4,7π/4),[-π/4,π/4)划分为四个象限,鼠标进入容器时的点的atan2(y,x)值在这四个象限里分别对应容器边框的下,右,上,左。如下图所示
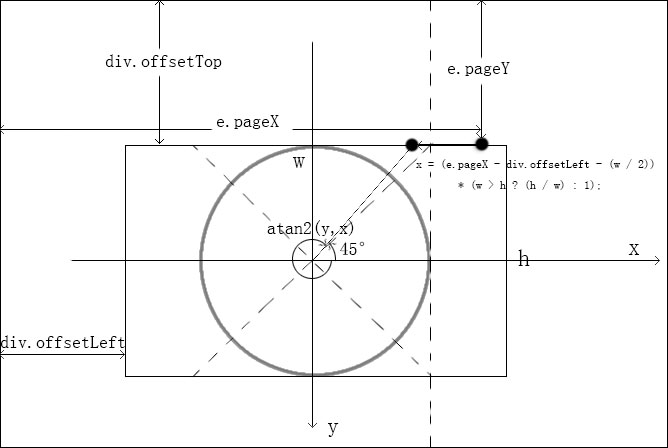
var x = (e.pageX - this.offsetLeft - (w / 2)) * (w > h ? (h / w) : 1);计算x坐标值时,如果点原来的x坐标的绝对值大于圆的半径值,则按 h/w 这个比例进行缩小,使得到的点的位置在容器的边界位置所对应的象限区间里。
y 坐标的计算也是一样。
var direction = Math.round((((Math.atan2(y, x) * (180 / Math.PI)) + 180) / 90) + 3) % 4;
((Math.atan2(y, x) * (180 / Math.PI)将点的坐标对应的弧度值换算成角度度数值,这里加上180并非必要,只是为了使得到的0,1,2,3能够与习惯性的上,右,下,左的位置对照,如果不加上180,得到的0,1,2,3就会分别对应下,右,上,左。
*修正:这里加上180不是并非必要的,而是在这个算法里必须的,因为atan2(y,x)返回值的范围是[-π,π],而不是我们习惯的[0,2π],负值会影响结果的正确性(比如右上和右下算出来的结果会不同),而且确实也使得得到的结果0,1,2,3的顺序符合了习惯(原作者可能没想这个,只是css里总是这个顺序,或许是我自己的习惯~)。
除以90,再取四舍五入值,是一个很精妙的用法,使得可以以45°为分界线。
分析完这个算法后,我内心有些激动。这里并没有用到什么高深的知识,即使是三角函数的基础知识都可以不知道(虽然初中就学了),但是可以用这么短短的三两行代码,就把我脑袋里浮现的那一长串的if else抛向云和山的彼端去,真的让我很难抑制内心的激动,深深的体会到算法之美,数学之美。
ps:以后一定要多多验证了再做结论,粗心不是个好态度啊!