带你掌握4种Python 排序算法

摘要：在编程里，排序是一个重要算法，它可以帮助我们更快、更容易地定位数据。在这篇文章中，我们将使用排序算法分类器对我们的数组进行排序，了解它们是如何工作的。

本文分享自华为云社区《Python 排序算法指南》，原文作者：唐里 。

在编程里，排序是一个重要算法，它可以帮助我们更快、更容易地定位数据。在这篇文章中，我们将使用排序算法分类器对我们的数组进行排序，了解它们是如何工作的。为了保障本文的可读性，这里只着重介绍4个排序算法。

• 冒泡排序
• 插入排序.
• 归并排序.
• 快速排序

冒泡排序

冒泡排序是一种简单的排序算法，它比较两个相邻对象的顺序，将非预期顺序的相邻对象位置交换。下面是它的工作步骤：

• 比较第一个和第二个对象，如果第一个大于第二个，将之交换。
• 将第二个对象和第三个对象进行比较，检查相同条件。以此类推直到比较到数组最后一个数。
• 重复执行这个过程，这样数组就按照从左到右从小到大排列了。

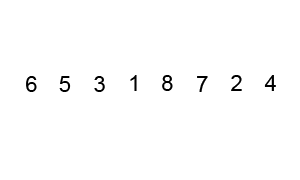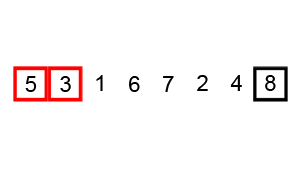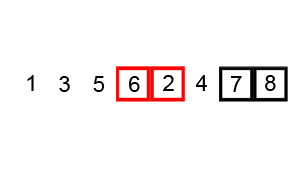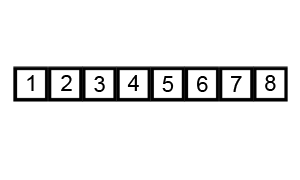
代码如下

# Python中的冒泡排序
def bubbleSort(array):
 
  # 外循环访问数组的每个元素
  for i in range(len(array)):

    # 内循环将数组元素与外循环迭代元素进行比较
    for j in range(0, len(array) - i - 1):

      # 比较两个相邻元素
      if array[j] > array[j + 1]:

        # 如果元素不是预期顺序则交换元素
        temp = array[j]
        array[j] = array[j+1]
        array[j+1] = temp
data = [5, 4, 3, 2, 1]

bubbleSort(data)
print('Sorted Array')
print(data)

#output: [1, 2, 3, 4, 5]

插入排序

插入排序也很简单，它分为已经排序和未排序两部分，将未排序部分的元素选中后正确放置在排序部分即可。类似卡牌游戏时我们手里有分类卡。下面是它的工作步骤：

• 遍历数组查找最低元素的索引并将其与数组的第一个元素交换。
• 找到数组(不包括第一个元素)中另一个最低的元素，并将其与第二个元素交换 ，然后重复操作，直到数组的最后一个元素。
• 这样，数组中最低的元素都会移到左边，而最大的元素会在数组的右边，因此数组是有序的。

代码如下

# Python中的排序算法
def insertionSort(array):
    for step in range(1, len(array)):
        key = array[step]
        j = step - 1
        # 将键与其左侧的每个元素进行比较，直到找到小于它的元素
        while j >= 0 and key < array[j]:
            array[j + 1] = array[j]
            j = j - 1
        # 将键放在比它小的元素之后。
        array[j + 1] = key

data = [11, 4, 3, 2, 12]

insertionSort(data)
print("sorted array")
print(data)

#output: [2, 3, 4, 11, 12]

归并排序

归并排序是基于分治算法原理的最常用的排序算法。我们将数组分为多个部分，然后对他们进行排序，最后将子部分合并为一个排序数组，为了更好的理解，下面是它的工作步骤：

• 把数组分成小块，直到每一块中没有单独的元素。
• 比较每一块数组，将最小值放在左侧，最大值放在数组的右侧。
• 如果觉得很难理解，看看这个动图。

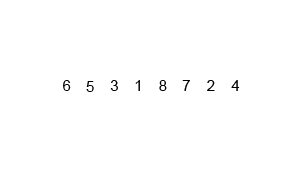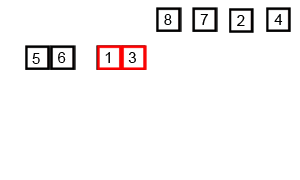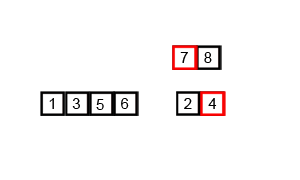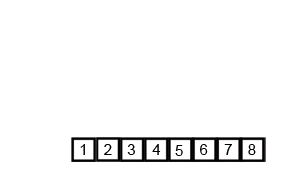
代码如下

# Python的归并排序
def mergeSort(array):
    if len(array) > 1:

        #  r 是将数组分为两半后的分割点
        r = len(array)//2
        L = array[:r]
        M = array[r:]

        # 通过递归方法对两半进行排序
        mergeSort(L)
        mergeSort(M)

        i = j = k = 0

        # 直到我们到达 L 或 M 的任一端，从中选择较大的元素 L 和 M 并将它们放置在 A[p 到 r] 处的正确位置
        while i < len(L) and j < len(M):
            if L[i] < M[j]:
                array[k] = L[i]
                i += 1
            else:
                array[k] = M[j]
                j += 1
            k += 1

        # 将L或者M里的元素排序好后，将剩余的元素并放入 A[p to r]
        while i < len(L):
            array[k] = L[i]
            i += 1
            k += 1

        while j < len(M):
            array[k] = M[j]
            j += 1
            k += 1
array = [8, 6, 14, 12, 10, 3]

mergeSort(array)
print("Sorted array: ")
print(array)

#output: [3, 6, 8, 10, 12, 14]

快速排序

与归并排序一样，快速排序也是基于分治算法的原理的一种排序算法。它选择一个元素作为枢轴，并围绕枢轴分区数组。下面是它的工作步骤：

• 选择一个转折点，这可以是随机选择的。这里假设我们选择数组的最后一个元素作为轴心。
• 将所有小于轴心的项目放在左侧，大于轴心的项目放在数组右侧。
• 在枢轴的左右两侧重复上面的步骤。

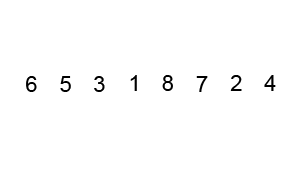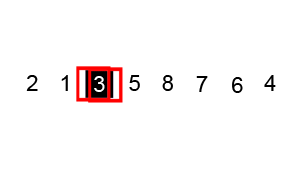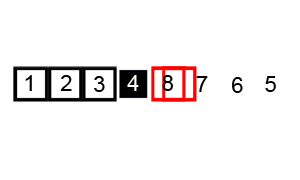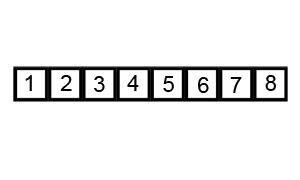
# Python中的快速排序
# 找到分区位置
def partition(array, lowest, highest):

  # 这里我们选择最右的元素作为枢轴
  pivot = array[highest]

  # 为最大的元素设置指针
  i = lowest - 1
  # 将每个元素与枢轴元素对比
  for j in range(lowest, highest):
    if array[j] <= pivot:
      i = i + 1
      # 将 i 处的元素与 j 处的元素交换
      (array[i], array[j]) = (array[j], array[i])

  # 将枢轴元素与 i 指定的较大元素交换
  (array[i + 1], array[highest]) = (array[highest], array[i + 1])

  # 返回分区完成的位置
  return i + 1
def quickSort(array, lowest, highest):
  if lowest < highest:

     # 找到枢轴元素
     # 小于枢轴的元素放左边
     # 大于枢轴的元素放右边
    pi = partition(array, lowest, highest)

    # 枢轴左侧的递归调用
    quickSort(array, lowest, pi - 1)

    # 枢轴右侧的递归调用
    quickSort(array, pi + 1, highest)
array = [9, 8, 3, 2, 1, 10, 7, 6, 19]

size = len(array)
quickSort(array, 0, size - 1)
print('Sorted Array is below')
print(array)

#output [1, 2, 3, 6, 7, 8, 9, 10, 19]

以上就是本文的全部内容，感谢阅读，如果对你有帮助希望点个赞~

原文地址：https://python.plainenglish.io/a-guide-to-sorting-algorithms-in-python-dfa9436b8527

点击关注，第一时间了解华为云新鲜技术~