摘要:对于队列来说数据结构相比栈复杂一些,但是也不是很难,搞懂先进先出然后用数组或者链表实现即可。
本文分享自华为云社区《手写各种队列,一文搞定》,原文作者:bigsai 。
前言
栈和队列是一对好兄弟,栈的机制相对简单,后入先出,就像进入一个狭小的山洞,山洞只有一个出入口,只能后进先出(在外面的先出去,堵在里面先进去的就有点倒霉)。而队列就好比是一个隧道,后面的人跟着前面走,前面人先出去(先入先出)。日常的排队就是队列运转形式的一个描述!
栈是一种喜新厌旧的数据结构,来了新的就会处理新的把老的先停滞在这(我们找人、约人办事最讨厌这种人),队列就是大公无私的一种数据结构,排队先来先得,讲究顺序性,所以这种数据结构在程序设计、中间件等都非常广泛的应用,例如消息队列、FIFO磁盘调度、二叉树层序遍历、BFS宽度优先搜索等等。
队列的核心理念就是:先进先出!
队列的概念:队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。

队列介绍
我们设计队列时候可以选择一个标准,这里就拿力扣622设计循环队列作为队列设计的标准。
队头front:删除数据的一端。
队尾rear :插入数据的一端。
对于数组,从数组后面插入更容易,数组前面插入较困难,所以一般用数组实现的队列队头在数组前面,队尾在数组后面;而对于链表,插入删除在两头分别进行那么头部(前面)删除尾部插入最方便的选择。
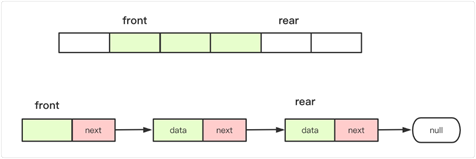
实现方法:
- MyCircularQueue(k): 构造器,设置队列长度为 k 。
- Front: 从队首获取元素。如果队列为空,返回 -1 。
- Rear: 获取队尾元素。如果队列为空,返回 -1 。
- enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
- deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
- isEmpty(): 检查循环队列是否为空。
- isFull(): 检查循环队列是否已满。
普通队列
按照上述的介绍,我们很容易知道数组实现的方式。用数组模拟表示队列。要考虑初始化,插入,问题。
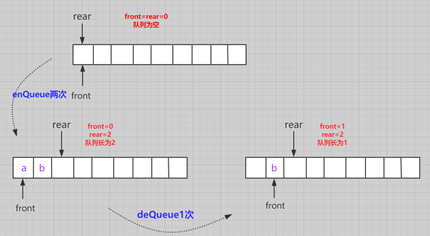
在这个普通队列一些操作需要注意的有:
初始化:数组的front和rear都指向0. (front和rear下标相等的时候说明队列为空)
入队:队不满,数组不越界,先队尾位置传值,再队尾下标+1(队尾rear实际上超前一位,为了区分空队列情况)
出队:队不空,先取队头位置元素,在队头+1。
但是很容易发现问题,每个空间域只能利用一次,造成空间极度浪费,非常容易越界!
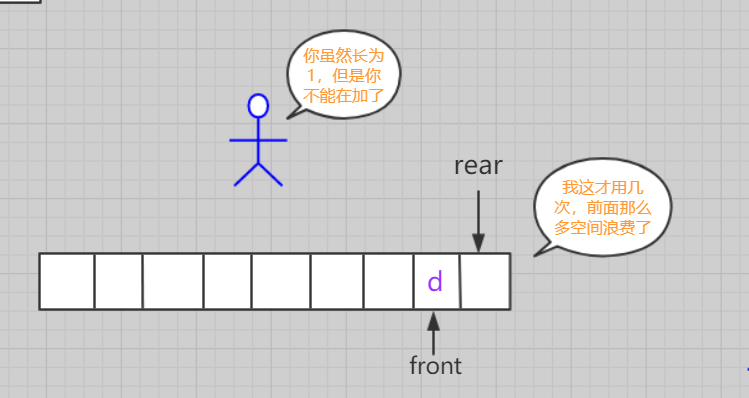
循环队列(数组实现)
针对上述的问题。有个较好的解决方法!就是对已经申请的(数组)内存重复利用。这就是我们所说的循环队列。循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
数组实现的循环队列就是在逻辑上作修改。因为我们队列中只需要front和rear两个指针。rear在逻辑上在后面,front在逻辑上是在前面的,但实际上它们不一定谁在前谁在后,在计算距离的时候需要给rear先补上数组长度减去front,然后求余即可。
初始化:数组的front和rear都指向0. 这里需要注意的是:front和rear位于同一个位置时候,证明队列里面是空的。还有在这里我具体实现时候将数组申请大了一个位置空出来,防止队列满的情况又造成front和rear在同一个位置。
入队:队不满,先队尾位置传值,再rear=(rear + 1) % maxsize;
出队:队不空,先取队头位置元素,front=(front + 1)% maxsize;
这里出队入队指标相加如果遇到最后需要转到头位置,这里直接+1求余找到位置(相比判断是否在最后更加简洁),其中maxsize是数组实际大小。
是否为空:return rear == front;
大小:return (rear+maxsize-front)%maxsize; 这里很容易理解,一张图就能解释清楚,无论是front实际在前在后都能满足要求。
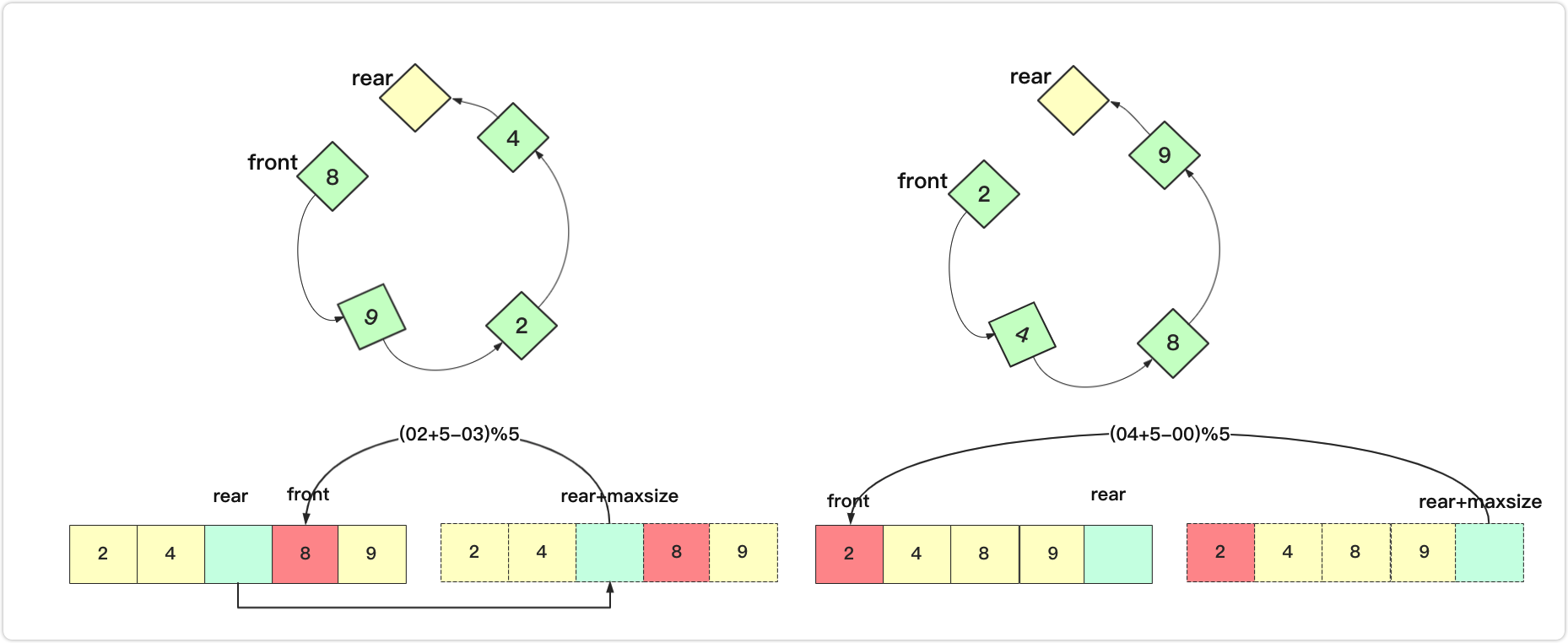
这里面有几个大家需要注意的,就是指标相加如果遇到最后需要转到头的话。可以判断是否到数组末尾位置。也可以直接+1求余。其中maxsize是数组实际大小。
具体实现:
public class MyCircularQueue { private int data[];// 数组容器 private int front;// 头 private int rear;// 尾 private int maxsize;// 最大长度 public MyCircularQueue(int k) { data = new int[k+1]; front = 0; rear = 0; maxsize = k+1; } public boolean enQueue(int value) { if (isFull()) return false; else { data[rear] = value; rear=(rear + 1) % maxsize; } return true; } public boolean deQueue() { if (isEmpty()) return false; else { front=(front+1)%maxsize; } return true; } public int Front() { if(isEmpty()) return -1; return data[front]; } public int Rear() { if(isEmpty()) return -1; return data[(rear-1+maxsize)%maxsize]; } public boolean isEmpty() { return rear == front; } public boolean isFull() { return (rear + 1) % maxsize == front; } }
循环队列(链表实现)
对于链表实现的队列,要根据先进先出的规则考虑头和尾的位置
我们知道队列是先进先出的,对于链表,我们能采用单链表尽量采用单链表,能方便尽量方便,同时还要兼顾效率。使用链表大概有两个实现方案:
方案一:如果队列头设在链表尾,队列尾设在链表头。那么队尾进队插入在链表头部插入没问题,容易实现,但是如果队头删除在链表尾部进行,如果不设置尾指针要遍历到队尾,但是设置尾指针删除需要将它前驱节点需要双向链表,都挺麻烦的。
方案二:如果队列头设在链表头,队列尾设在链表尾,那么队尾进队插入在链表尾部插入没问题(用尾指针可以直接指向next),容易实现,如果队头删除在链表头部进行也很容易,就是我们前面常说的头节点删除节点。
所以我们最终采取的是方案2的带头节点、带尾指针的单链表!
主要操作为:
初始化:设立一个头结点,是front和rear都先指向它。
入队:rear.next=va;rear=va;(va为被插入节点)

出队:队不空,front.next=front.next.next;经典带头节点删除,但是如果仅有一个节点删除时候,需要多加一个rear=front,不然rear就失联啦。
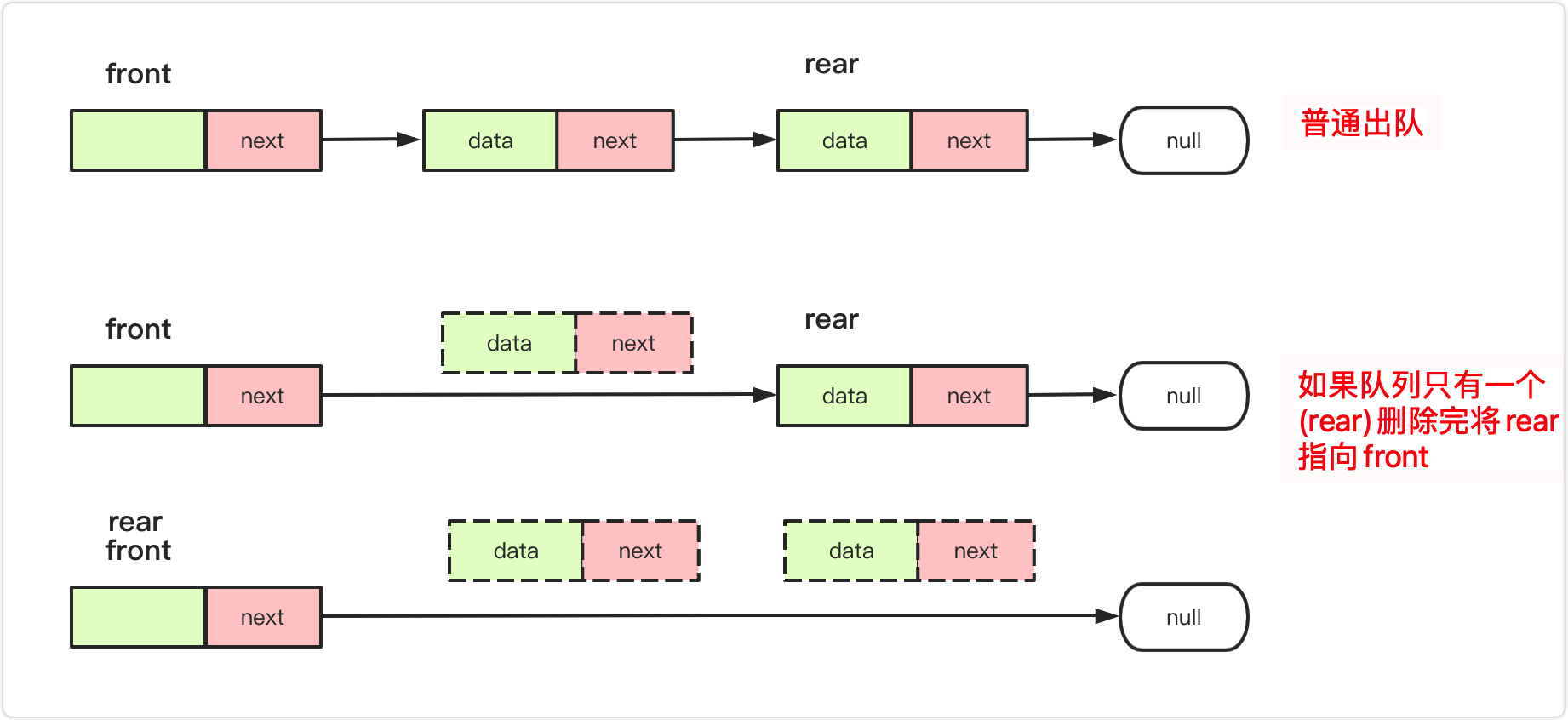
是否为空:return rear == front; 或者自定义维护len判断return len==0
大小:节点front遍历到rear的个数,或者自定义维护len直接返回(这里并没实现)。
实现代码:
public class MyCircularQueue{ class node { int data;// 节点的结果 node next;// 下一个连接的节点 public node() {} public node(int data) { this.data = data; } } node front;//相当于head 带头节点的 node rear;//相当于tail/end int maxsize;//最大长度 int len=0; public MyCircularQueue(int k) { front=new node(0); rear=front; maxsize=k; len=0; } public boolean enQueue(int value) { if (isFull()) return false; else { node va=new node(value); rear.next=va; rear=va; len++; } return true; } public boolean deQueue() { if (isEmpty()) return false; else { front.next=front.next.next; len--; //注意 如果被删完 需要将rear指向front if(len==0) rear=front; } return true; } public int Front() { if(isEmpty()) return -1; return front.next.data; } public int Rear() { if(isEmpty()) return -1; return rear.data; } public boolean isEmpty() { return len==0; //return rear == front; } public boolean isFull() { return len==maxsize; } }
双向队列(加餐)
设计实现双端队列,其实你经常使用的ArrayDeque就是一个经典的双向队列,其基于数组实现,效率非常高。我们这里实现的双向队列模板基于力扣641 设计循环双端队列 。
你的实现需要支持以下操作:
- MyCircularDeque(k):构造函数,双端队列的大小为k。
- insertFront():将一个元素添加到双端队列头部。 如果操作成功返回 true。
- insertLast():将一个元素添加到双端队列尾部。如果操作成功返回 true。
- deleteFront():从双端队列头部删除一个元素。 如果操作成功返回 true。
- deleteLast():从双端队列尾部删除一个元素。如果操作成功返回 true。
- getFront():从双端队列头部获得一个元素。如果双端队列为空,返回 -1。
- getRear():获得双端队列的最后一个元素。 如果双端队列为空,返回 -1。
- isEmpty():检查双端队列是否为空。
- isFull():检查双端队列是否满了。
其实有了上面的基础,实现一个双端队列非常容易,有很多操作和单端的循环队列是一致的,只有多了一个队头插入和队尾删除的操作,两个操作分别简单的分析一下:
队头插入:队友front下标位置本身是有值的,所以要将front退后一位然后再赋值,不过要考虑是否为满或者数组越界情况。
队尾删除:只需要rear位置减1,同时也要考虑是否为空和越界情况。
具体实现代码:
public class MyCircularDeque { private int data[];// 数组容器 private int front;// 头 private int rear;// 尾 private int maxsize;// 最大长度 /*初始化 最大大小为k */ public MyCircularDeque(int k) { data = new int[k+1]; front = 0; rear = 0; maxsize = k+1; } /** 头部插入 */ public boolean insertFront(int value) { if(isFull()) return false; else { front=(front+maxsize-1)%maxsize; data[front]=value; } return true; } /** 尾部插入 */ public boolean insertLast(int value) { if(isFull()) return false; else{ data[rear]=value; rear=(rear+1)%maxsize; } return true; } /** 正常头部删除 */ public boolean deleteFront() { if (isEmpty()) return false; else { front=(front+1)%maxsize; } return true; } /** 尾部删除 */ public boolean deleteLast() { if(isEmpty()) return false; else { rear=(rear+maxsize-1)%maxsize; } return true; } /** Get the front item */ public int getFront() { if(isEmpty()) return -1; return data[front]; } /** Get the last item from the deque. */ public int getRear() { if(isEmpty()) return -1; return data[(rear-1+maxsize)%maxsize]; } /** Checks whether the circular deque is empty or not. */ public boolean isEmpty() { return front==rear; } /** Checks whether the circular deque is full or not. */ public boolean isFull() { return (rear+1)%maxsize==front; } }
总结
对于队列来说数据结构相比栈复杂一些,但是也不是很难,搞懂先进先出然后用数组或者链表实现即可。
对于数组,队尾tail指向的位置是空的,而链表的front(head一样)为头指针为空的,所以在不同结构实现相同效果的方法需要注意一下。
数组实现的循环队列能够很大程度利用数组空间,而双向队列则是既能当队列又能当栈的一种高效数据结构,掌握还是很有必要的。