Tarjan：这个算法大神

摘要：图的算法是进行静态分析的基础数据算法，如何提高图的分析效率，就需要对图的算法有进一步的认识。

1. 引言

在静态分析技术中, 我们常用会将代码转成抽象语法树(AST), 然后采用深度遍历（DFS）来完成对语法树的遍历和查询，找到潜在的问题缺陷。

对于语义的分析，我们采用的控制流和数据流也都无一例外的采用了以图为基础的算法, 通过图的可达性, 来完成变量、表达式的可达分析, 以及变量的依赖分析、值流图等等。

图的算法是进行静态分析的基础数据算法，如何提高图的分析效率，就需要对图的算法有进一步的认识。

1.1. 故事从1986年的图灵奖说起

1986年的图灵奖是John E.Hoperoft和Robert E·Tarjan两人共同获得， 而且Robert E·Tarjan曾是John E.Hoperoft的学生,他们的密切合作取得了算法设计与分析方面的卓越贡献, 赢得了1986年度美国计算机协会（Association for Computing Machinery, ACM）图灵奖的荣誉。

1.2. 故事的前半段

在领奖的时候，John E.Hopcroft 做了一个“计算机科学:一门学科的出现” 的演讲， 从他自己的经历出发，展现了计算科学在那个风起云涌的年代形成的过程。

时间回到1964年，计算机才刚刚成为一门学科， 普林斯顿大学一个偶然的邀请，使本打算到美国西海岸教授电器工程的Hoperoft改变了自己的人生轨迹，从此投入到了计算机科学的研究。

那个时候，计算机科学的大部分课程的内容都是围绕着数字计算机电路的设计以及如何减少构造这些电路所需要的晶体管数展开的。然而, 到了六十年代中期, 技术的进步已使得晶体管马上就要被每片有多达几百个元件的计算机芯片所取代。因此, 减少晶体管数再没有么意义，那时所谓的计算机科学的课程即将过时, 必须发展新的课程。

Hopcroft 并没有接受过正规计算机教育，只是他在斯坦福大学读电器工程学博士的时候，上过David Huffman（霍夫曼编码的发明者）教的一门计算机课程，学习了开关电路、逻辑设计以及计算理论的基本知识。普林斯顿要Hoperoft在自动机理论方面开设一门新的课程，当时没有任何教程可以参考, 只给了他推荐了6篇论文。 其中包括：

• 1943年,McCulloch和Pitts发表的一篇关于用来描述神经网络中活动的逻辑演算的论文。这些活动是一系列的电脉冲, 并能看作是0-1串。论文提出了一种描述神经网中的0-1串是如何结合以产生新的0-1串的方法。这种描述方法后来被发展成为一种描述串集的正则表达式语言。
• 数学家Michael Rabin和Dana Scott提出的一种具有有限量存储其的计算机模型，这个模型就是有限状态自动机。并证明了有限状态自动机的可能的行为和正则表达式所描述的行为的一致性。 数学和计算机学思想的汇集，使计算机科学家相信正则语言和有限自动机的重要性。
• 语言学家Chomsky研究发展的一种前后文无关文法的概念。这与Backus和Naur为描述各种程序设计语言的语法而发展的一套形式表示法惊人的等价。
• 图灵于1963年引入了一种简单的计算装置模型,现在称做图灵机。并论证了能够进行的任何计算过程都能在图灵机上编程序实现。图灵机是现代可计算理论的基础。
• 数学家Hartmanis和Stearns采用算法的执行步数来度量算法的复杂性，并使这一方法发展了一种复杂性分类的理论。

1967年，Hopcroft转去康奈尔大学，转而研究算法与数据结构。他相信理论计算机科学的方法学，可以用来为算法设计发展一种科学基础,这对于实践者将是很有用的。

在七十年代初期, Hopcroft在斯坦福大学度过了一年的假期, 在那里遇到Robert Tarjan并与他同用一间办公室, Tarjan那时是二年级研究生。获得这次图灵奖的研究就是在那段合作时间里作的。

Hopcroft 在发言的最后，还不忘呼吁，为了保持美国取得的技术和经济的领导地位，必须对计算机科学进行全国性的投入和支持。

1.3. 故事的后半段

说到Tarjan，他在图论算法和数据结构领域有很大的贡献。 下面对这个大牛也做个简单的介绍。

Tarjan在1969年获得了加州理工学院数学学士学位。在斯坦福大学，他获得了他的计算机科学硕士学位（1971）和博士学位(1972). Tarjan从1985年开始任教于普林斯顿大学。

Tarjan还拥有很多研究所和公司的工作经验， 例如：AT&T贝尔实验室、NEC研究所、InterTrust Technologies、康柏、惠普、微软等。

Tarjan是一个非常高产的计算机科学家，从计算机科学出版物在线参考网站dblp收集的有关他发表在的杂志、会议和出版物，多达300+。

他独立研究的算法有：Tarjan离线的LCA算法（一种优秀的求最近公共祖先的线性离线算法）、Tarjan强连通分量算法（甚至比后来才发表的Kosaraju算法平均要快30%）、Hopcroft-Tarjan算法（第一个平面性测试的线性算法）。

他还开发了一些重要的数据结构，比如斐波那契堆（Fibonacci Heap，插入查询合并O(1)，删除O(logn)的强大数据结构）、伸展树（Splay Tree，和另外一位计算机科学家共同发明）、动态树（Link-Cut Tree，发明人之一）。

下图是他普林斯顿大学个人简介中的一个插图， 这个是他的另一个重要的研究领域：自适应搜索树的查询(self-adjusting search tree)，在树的遍历过程中，改变树的结构以提高树的搜索效率。

他的主要荣誉：

• 1986年，与John Hopcroft分享了当年的图灵奖，原因是对算法和数据结构的设计分析做出的地基式的贡献；
• 1994年，被选为美国计算机协会（Association for Computing Machinery, ACM）院士；
• 2004年，欧洲科学院的Blaise Pascal数学和计算机科学奖章；
• 1983年，Rolf Nevanlinna奖的第一个获奖者，国际数学联盟在信息科学的数学方面的杰出贡献而每四年获奖一次；

2. Tarjan算法

图的一些基本概念：

• 关联（incident）：点为边的端点;
• 邻接（adjacent）：点与点关联同一条边，或边与边关联同一顶点；
• 子图：图G'的点和边都是图G的子集，则G'为G的子图;
• 道路：从点v到点u的路径；
• 简单道路：没有重复边的道路；
• 回路：起点与终点相同的道路；
• 简单回路：没有重复边的回路；
• 连通：两顶点间有道路；
• 强连通：有向图u→v与v→u都有道路；
• 连通图：任意两顶点间都有道路（若有向图除去方向后连通，则称有向图连通）；
• 简单图：没有重复边和自环的图；
• 完全图：任意两顶点间有一条边到达的简单图（有向完全图与无向完全图）；
• 强连通（strongly connected）: 在有向图G 中，如果两个顶点间至少存在一条路径，称两个顶点强连通（strongly connected）；
• 强连通图: 如果有向图G 的每两个顶点都强连通，称G 是一个强连通图；
• 强连通分量(strongly connected components): 非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

求强连通分量就是我们今天要解决的问题，根据强连通分量定义，用双向遍历取交集的方法求强连通分量，时间复杂度为O（$N^2$+M）. 而Tarjan或Kosaraju算法, 两者的时间复杂度都是O（N+M）。

2.1. 算法简介

Tarjan 算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

• 定义:
• DFN(u)为节点u 搜索的次序编号(时间戳);
• LOW(u)为u 或 u的子树能够追溯到的最早的栈中节点的次序号;
  由定义可以得出，当 DFN(u)=LOW(u)时，以u为根的搜索子树上所有节点是一个强连通分量。
• 算法：

（1）当首次搜索到点u时DFN[u]=LOW[u]=time;

（2）每当搜索到一个点，把该点压入栈顶;

（3）当u和v有边相连时:

1. 如果v不在栈中（树枝边），DFS(v)，并且LOW[u] = min{LOW(u),LOW(v)};
2. 如果v在栈中（前向边/后向边），此时LOW[u] = min{LOW[u],DFN[v]}

（4）当DFN[u]=LOW[u]时，将它以及在它之上的元素弹出栈，此时，弹出栈的结点构成一个强连通分量;

（5）继续搜索，知道图被遍历完毕。

由于在这个过程中每个点只被访问一次，每条边也只被访问一次，所以Tarjan算法的时间复杂度是O(n+m).

2.2. 算法伪代码

tarjan(u){
  DFN[u]=LOW[u]=++Index                      // (1) 为节点u设定次序编号和Low初值
  Stack.push(u)                              // (2) 将节点u压入栈中
  for each (u, v) in E                       // (3) 枚举每一条边
    if (v is not visted)                     // (4) 如果节点v未被访问过
      tarjan(v)                              // (5) 继续向下找
      LOW[u] = min(LOW[u], LOW[v])           // (6) 
    else if (v in Stack)                     // (7) 如果节点v还在栈内
      LOW[u] = min(LOW[u], DFN[v])           // (8)

  if (DFN[u] == LOW[u])                      // (9) 如果节点u是强连通分量的根
    repeat                                   // (10) 循环出栈,直到u=v
      v = Stack.pop                          // (11) 将v退栈，为该强连通分量中一个顶点
      print v                                // (12) 输出v
    until (u == v)                           // (13) 循环终止条件u=v  
}

2.3. 举例演算

0. 求下面有向图的强连通分量

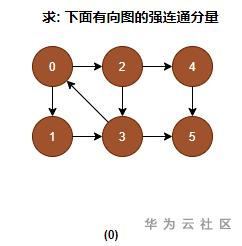
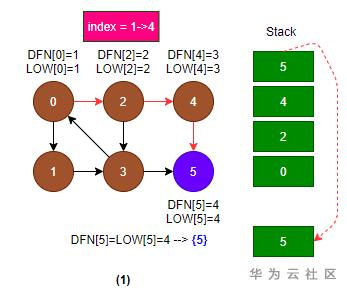
1. 从节点0开始DFS:

• 代码(1)-(5): 得到访问链:0 -> 2 -> 4 -> 5, 把遍历到的4个节点{0, 2, 4, 5}加入栈中; 四个节点的LOW[] 和 DFN[]值, 依次被Index标注成1到4; 注: 这里也可以走另外一条路径: 0 -> 2 -> 3 -> 5;
• 代码(9)-(13): 节点5的后续边已经遍历完成, 退出节点5时, 发现DFN[5] = LOW[5] = 4, 于是节点5出栈，{5}为一个强连通分量;

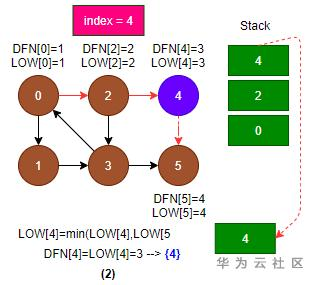
2. 返回节点4:

• 代码(6): LOW[4] = min(LOW[4], LOW[5]) = min(3, 4) = 3;
• 代码(9)-(13): 节点4的后续边已经遍历完成, 退出节点4时, DFN[4] = LOW[4] = 3; 退栈到节点4出栈，{4}为一个强连通分量;

3. 返回节点2:

• 代码(6): LOW[2] = min(LOW[2], LOW[4]) = min(2, 3) = 2;

4. 从节点2继续搜索到节点3:

• 代码(4)-(5): 继续遍历节点2的后续边, 找到节点3;
• 代码(1)-(2): 把3加入堆栈, Index = 5, DFN[3] = LOW[3] = 5;
• 代码(3)-(8): 发现节点3向节点0有边(3 -> 0)，且节点0在栈中，所以LOW[3] = min(LOW[3], DFN[0]) = min(5, 1) = 1。
• 代码(3)-(8): 发现节点3向节点5有边(3 -> 5), 但节点5已出栈;

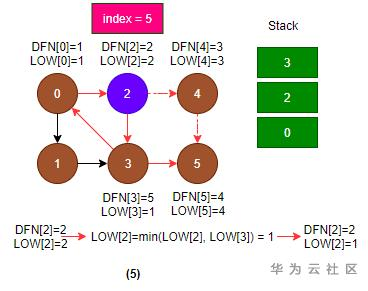
5. 返回节点2;

• 代码(6): LOW[2] = min(LOW[2], LOW[3]) = min(2, 1) = 1;

6. 返回节点0;

• 代码(6): LOW[0] = min(LOW[0], LOW[2]) = min(1, 1) = 1;

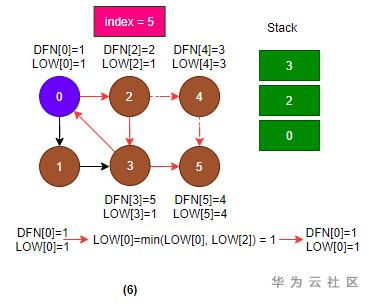
7. 从节点0继续搜索到节点1;

• 代码(1)-(2): 把1加入堆栈, Index = 6, DFN[1] = LOW[1] = 6;
• 代码(3)-(8): 发现节点1向节点3有边(1 -> 3)，且节点3还在栈中，所以LOW[1] = min(LOW[1], DFN[3]) = min(6, 5) = 5;

8. 返回节点0;

• 代码(9)-(13): 退出时发现DFN[0] = LOW[0] = 1, 退栈到节点0出栈，组成一个连通分量{1, 3, 2, 0}。

• 最终, 所有节点和边都已经访问到, 得到所有连通分量: {5}, {4}, {1, 3, 2, 0}。
• 枚举边的时候, 与输入顺序相关, 可能计算顺序不同, 但过程中每个点只被访问一次，每条边也只被访问一次，所以总的结论一致.

2.4. Kosaraju算法

Kosaraju是基于对有向图及其逆图两次DFS的方法，其时间复杂度也是 O(N+M)。与Trajan算法相比，Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS，不用建立逆图，更简洁。
在实际的测试中，Tarjan算法的运行效率也比Kosaraju算法高30%左右。

3. Tarjan算法实现

为了便于后期的扩展, 适用更为广泛的图运算。 这里算法的实现中，图的表示采用了Google guava库中的common.graph, 你需要在pom.xml 中加入guava的依赖包如下:

   <!-- https://mvnrepository.com/artifact/com.google.guava/guava -->
    <dependency>
        <groupId>com.google.guava</groupId>
        <artifactId>guava</artifactId>
        <version>30.1-jre</version>
    </dependency>

为了和举例中图的特征保持一致, 图结构采用guava里的MutableGraph graph, Integer的值表示结点的编号。 例如 graph.putEdge(0, 2); 表示增加一条有向边, 从结点0 指向 结点2, graph 会判断结点0 和2 是否存在结点中存在, 如不存在, 则会增加相应的结点。

大家可以根据自己的需要采用不同的图结构。

• 目前我们常用的图基础数据结构:
• JUNG: 2016.9.8 - 2.1.1. 据说作者正在打算采用google 的guava 重写这个工程;
• JGraphT: 2020.6.15 - 1.5.0. 这个是目前很活跃的一个图基础数据包, 里面也实现Tarjan算法, 后面有时间去看下具体的实现。 Maven依赖的引用如下:

<!-- https://mvnrepository.com/artifact/org.jgrapht/jgrapht-core -->
<dependency>
    <groupId>org.jgrapht</groupId>
    <artifactId>jgrapht-core</artifactId>
    <version>1.5.0</version>
</dependency>

3.1. 算法代码

package sdong.graph.utils;
​
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;
​
import com.google.common.graph.MutableGraph;
​
public class Tarjan {
    // 输入信息
    private MutableGraph<Integer> graph;
​
    // 输出信息
    private List<List<Integer>> sccsList = new ArrayList<List<Integer>>(); // 保存强连通分量(Sccs)
​
    private int[] DFN; // DFN(u)为节点u 搜索的次序编号(时间戳)
    private int[] LOW; // LOW(u)为u 或u 的子树能够追溯到的最早的栈中节点的次序号
    private int index; // 搜索的次序编号(时间戳)
​
    private Stack<Integer> stack; // 栈, 用于回退节点
    private boolean[] isInStack; // 节点是否在栈内，减少栈中结点的判断
​
    /**
     * 构造函数
     * 
     * @param graph 图
     */
    public Tarjan(MutableGraph<Integer> graph) {
        this.graph = graph;
​
        int numOfNode = graph.nodes().size();
        DFN = new int[numOfNode];
        LOW = new int[numOfNode];
​
        // 初始化DFN、LOW所有元素都置为-1；DFN[u]=-1，代表节点u还有没被访问过
        Arrays.fill(DFN, -1);
        Arrays.fill(LOW, -1);
​
        this.stack = new Stack<Integer>();
        this.isInStack = new boolean[numOfNode];
    }
​
    /**
     * 遍历图节点
     * 
     * @return 强连通分量
     */
    public List<List<Integer>> reverse() {
        for (int i = 0; i < graph.nodes().size(); i++) {
            if (DFN[i] == -1) {
                tarjan(i);
            }
        }
        return sccsList;
    }
​
    /**
     * Tarjan算法
     * 
     * @param curNode 当前节点
     */
    public void tarjan(int curNode) {
        // 初始化搜索的次序编号(时间戳)
        DFN[curNode] = LOW[curNode] = ++index;
​
        // 入栈
        stack.push(curNode);
        isInStack[curNode] = true;
​
        // 遍历后继节点
        for (Integer succNode : graph.successors(curNode)) {
            if (DFN[succNode] == -1) { // 如果没被访问过（-1代表没有被访问）
                tarjan(succNode); // 递归调用
                LOW[curNode] = Math.min(LOW[curNode], LOW[succNode]); // 更新所能到的上层节点
            } else if (isInStack[succNode]) { // 如果在栈中,并且被访问过
                LOW[curNode] = Math.min(LOW[curNode], DFN[succNode]); // 到栈中最上端的节点
            }
        }
​
        // 发现是整个强连通分量子树里的最小根
        List<Integer> scc = new ArrayList<Integer>();
        if (LOW[curNode] == DFN[curNode]) {
            // 出栈
            int j = -1;         
            while (curNode != j) {
                j = stack.pop();
                isInStack[j] = false;
                scc.add(j);
            }
            sccsList.add(scc);
        }
    }
}

3.2. 验证代码

验证代码使用junit完成结果的验证。生成可变图graph里面的: incidentEdgeOrder(ElementOrder.stable()), 是为了保证关联边的读取时和输入的顺序一致, 以便得到和前面演算过程的一致性的结果.

package sdong.graph.utils;
​
import static org.junit.Assert.assertEquals;
​
import java.util.List;
​
import com.google.common.graph.ElementOrder;
import com.google.common.graph.GraphBuilder;
import com.google.common.graph.MutableGraph;
​
import org.junit.Test;
​
import sdong.graph.utils.Tarjan;
​
public class TarjanTest {
​
    @Test
    public void reverseTestGuava(){
        MutableGraph<Integer> graph = GraphBuilder.directed().incidentEdgeOrder(ElementOrder.stable()).build();
        graph.putEdge(0, 2);
        graph.putEdge(0, 1);
        graph.putEdge(1, 3);
        graph.putEdge(2, 4);
        graph.putEdge(2, 3);
        graph.putEdge(3, 0);
        graph.putEdge(3, 5);
        graph.putEdge(4, 5);
 
        Tarjan tarjan = new Tarjan(graph);
        List<List<Integer>> result = tarjan.reverse(); 
        // 校验
        assertEquals(3, result.size());
        assertEquals("[5]", result.get(0).toString());
        assertEquals("[4]", result.get(1).toString());
        assertEquals("[1, 3, 2, 0]", result.get(2).toString()); 
    }
}

4. 结论

• 计算机科学是一个综合性的学科;
• 基础科学的研究论文的重要性, 不仅在于其技术方面的贡献, 更重要的是它们提供一种概念上的见解或者一种研究范例；
• 基础科学对一个国家很重要；
• 计算机科学对一个国家很重要。

5. 参考

1. John E.Hoperoft 简介
2. 1986年图灵奖John E.Hoperoft发言：COMPUTER SCIENCE: THE EMERGENCE OF A DISCIPLINE
3. Robert Endre Tarjan 简介
4. dblp - Robert Endre Tarjan
5. Depth-First Search and Linear Graph Algorithms
6. Guava Grpah

本文分享自华为云社区《史上最清晰的Tarjan算法详解》，原文作者：Uncle_Tom。

 

点击关注，第一时间了解华为云新鲜技术~