快速排序【转】

来源：http://blog.csdn.net/cjf_iceking/article/details/7925470

还记得曾哥淡定的哼唱"七月份的前奏是狮子座~，八月份的尾巴也是狮子座~'，狮子座的尾巴也是校园招聘的开始，祝愿毕业生们都能够找到满意的工作。如果你拿到太多的offer难以选择的时候，那就给每一份offer定上各项指标，算出权值，最后再用效率超高的快速排序来进行排序。

一. 算法描述

快速排序：快速排序采用分治法进行排序，首先是分割，选取数组中的任意一个元素value（默认选用第一个），将数组划分为两段，前一段小于value，后一段大于value；然后再分别对前半段和后半段进行递归快速排序。其实现细节如下图所示：

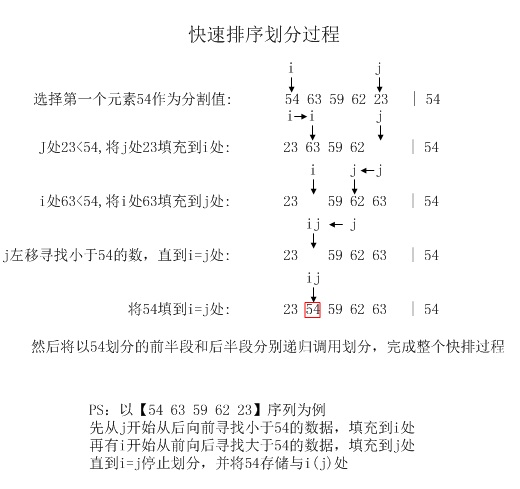
二. 算法分析

平均时间复杂度：O(nlog₂n)

空间复杂度：O(n)

稳定性：不稳定

三. 算法实现

 1 /********************************************************
 2 *函数名称：Split
 3 *参数说明：pDataArray 无序数组；
 4 *           iBegin为pDataArray需要快速排序的起始位置
 5 *          iEnd为pDataArray需要快速排序的结束位置
 6 *函数返回：分割后的分割数位置
 7 *说明：    以iBegin处的数值value作为分割数，
 8            使其前半段小于value，后半段大于value
 9 *********************************************************/
10 int Split(int *pDataArray,int iBegin,int iEnd)
11 {
12     int pData = pDataArray[iBegin];    //将iBegin处的值作为划分值
13 
14     while (iBegin < iEnd)    //循环分割数组，使其前半段小于pData，后半段大于pData
15     {
16         while (iEnd > iBegin && pDataArray[iEnd] >= pData)    //从后向前寻找小于pData的数据位置
17             iEnd--;
18 
19         if (iEnd != iBegin)
20         {
21             pDataArray[iBegin] = pDataArray[iEnd];    //将小于pData数据存放到数组前方
22             iBegin++;
23 
24             while (iBegin < iEnd && pDataArray[iBegin] <= pData)
25                 iBegin++;
26             
27             if (iBegin != iEnd)
28             {
29                 pDataArray[iEnd] = pDataArray[iBegin];    //将大于pData数据存放到数组后方
30                 iEnd--;
31             }
32         }
33     }
34 
35     pDataArray[iEnd] = pData;    //此时iBegin=iEnd，此处存储分割数据pData
36     return iEnd;
37 }
38 
39 /********************************************************
40 *函数名称：QSort
41 *参数说明：pDataArray 无序数组；
42 *           iBegin为pDataArray需要快速排序的起始位置
43 *          iEnd为pDataArray需要快速排序的结束位置
44 *说明：    快速排序递归函数
45 *********************************************************/
46 void QSort(int* pDataArray, int iBegin, int iEnd)
47 {
48     if (iBegin < iEnd)
49     {
50         int pos = Split(pDataArray, iBegin, iEnd);    //获得分割后的位置
51         QSort(pDataArray, iBegin, pos - 1);           //对分割后的前半段递归快排
52         QSort(pDataArray, pos + 1, iEnd);             //对分割后的后半段递归快排
53     }
54 }
55 
56 /********************************************************
57 *函数名称：QuickSort
58 *参数说明：pDataArray 无序数组；
59 *           iDataNum为无序数据个数
60 *说明：    快速排序
61 *********************************************************/
62 void QuickSort(int* pDataArray, int iDataNum)
63 {
64     QSort(pDataArray, 0, iDataNum - 1);
65 }

View Code

四. 算法优化

快排选用数组第一个元素作为分割元素，如果是一个已经基本有序的数组，那么时间复杂度将会提升到O(n²)；可以从数组中随机选择一个元素作为划分数据，这样即使针对基本有序的数据来说，效率同样达到(nlog₂n)，优化后分割函数如下所示：

 1 int Split(int *pDataArray,int iBegin,int iEnd)
 2 {
 3     int rIndex = rand() % (iEnd - iBegin + 1);    //随机获得偏移位置
 4 
 5     int pData = pDataArray[iBegin + rIndex];    //将iBegin+rIndex处的值作为划分值
 6 
 7     while (iBegin < iEnd)    //循环分割数组，使其前半段小于pData，后半段大于pData
 8     {
 9         while (iEnd > iBegin && pDataArray[iEnd] >= pData)    //从后向前寻找小于pData的数据位置
10             iEnd--;
11 
12         if (iEnd != iBegin)
13         {
14             pDataArray[iBegin] = pDataArray[iEnd];    //将小于pData数据存放到数组前方
15             iBegin++;
16 
17             while (iBegin < iEnd && pDataArray[iBegin] <= pData)
18                 iBegin++;
19             
20             if (iBegin != iEnd)
21             {
22                 pDataArray[iEnd] = pDataArray[iBegin];    //将大于pData数据存放到数组后方
23                 iEnd--;
24             }
25         }
26     }
27 
28     pDataArray[iEnd] = pData;    //此时iBegin=iEnd，此处存储分割数据pData
29     return iEnd;
30 }