题目描述
为了得到书法大家的真传,小 E 同学下定决心去拜访住在魔法森林中的隐 士。魔法森林可以被看成一个包含 n 个节点 m 条边的无向图,节点标号为 1,2,3,…,n,边标号为 1,2,3,…,m。初始时小 E 同学在 1 号节点,隐士则住在 n 号节点。小 E 需要通过这一片魔法森林,才能够拜访到隐士。
魔法森林中居住了一些妖怪。每当有人经过一条边的时候,这条边上的妖怪 就会对其发起攻击。幸运的是,在 1 号节点住着两种守护精灵:A 型守护精灵与 B 型守护精灵。小 E 可以借助它们的力量,达到自己的目的。
只要小 E 带上足够多的守护精灵,妖怪们就不会发起攻击了。具体来说,无 向图中的每一条边 ei 包含两个权值 ai 与 bi 。若身上携带的 A 型守护精灵个数不 少于 ai ,且 B 型守护精灵个数不少于 bi ,这条边上的妖怪就不会对通过这条边 的人发起攻击。当且仅当通过这片魔法森林的过程中没有任意一条边的妖怪向 小 E 发起攻击,他才能成功找到隐士。
由于携带守护精灵是一件非常麻烦的事,小 E 想要知道,要能够成功拜访到 隐士,最少需要携带守护精灵的总个数。守护精灵的总个数为 A 型守护精灵的 个数与 B 型守护精灵的个数之和。
输入输出格式
输入格式:
输入文件的第 1 行包含两个整数 n,m,表示无向图共有 n 个节点,m 条边。 接下来 m 行,第i+ 1 行包含 4 个正整数 Xi,Yi,ai,bi,描述第i条无向边。 其中Xi与 Yi为该边两个端点的标号,ai 与 bi 的含义如题所述。 注意数据中可能包含重边与自环。
输出格式:
输出一行一个整数:如果小 E 可以成功拜访到隐士,输出小 E 最少需要携 带的守护精灵的总个数;如果无论如何小 E 都无法拜访到隐士,输出“-1”(不 含引号)。
输入输出样例
4 5 1 2 19 1 2 3 8 12 2 4 12 15 1 3 17 8 3 4 1 17
32
3 1 1 2 1 1
-1
说明
- 解释1
如果小 E 走路径 1→2→4,需要携带 19+15=34 个守护精灵; 如果小 E 走路径 1→3→4,需要携带 17+17=34 个守护精灵; 如果小 E 走路径 1→2→3→4,需要携带 19+17=36 个守护精灵; 如果小 E 走路径 1→3→2→4,需要携带 17+15=32 个守护精灵。 综上所述,小 E 最少需要携带 32 个守护精灵。
- 解释2
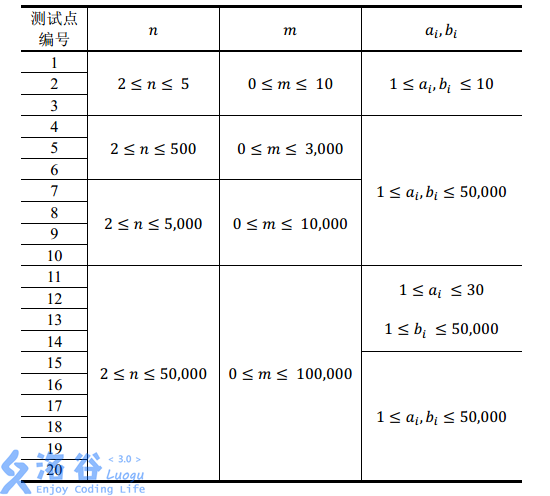
题解:
每条边有两个权值,合在一起维护十分不便,考虑将它们分开。
将所有边按权值a从小到大排序,每一次加入一条边,找一下1~n的所有路径中权值b的最大值的最小值,然后用amax+bmax更新答案。
为什么这样做是对的呢,如果bmax所在的路径并不是amax所在的路径,那么我们在放入amax之前,bmax就已经和一个比amax要小的权值更新了答案,所以更优解已经被计算在内了。
然后每次SPFA不需要memset,直接将当前加入的边的两端点入队就好。
这道题没有设计卡SPFA的数据,所以SPFA可以水过去。
1 //Never forget why you start 2 #include<iostream> 3 #include<cstdio> 4 #include<cstdlib> 5 #include<cstring> 6 #include<cmath> 7 #include<algorithm> 8 #include<queue> 9 #define inf (2000000000) 10 using namespace std; 11 int n,m,ans=inf; 12 queue<int>mem; 13 struct Edge{ 14 int from,to,dis1,dis2; 15 }e[100005]; 16 struct node{ 17 int next,to,dis1,dis2; 18 }edge[200005]; 19 int head[50005],size; 20 void putin(int from,int to,int dis1,int dis2){ 21 size++; 22 edge[size].next=head[from]; 23 edge[size].to=to; 24 edge[size].dis1=dis1; 25 edge[size].dis2=dis2; 26 head[from]=size; 27 } 28 int dist[50005]; 29 bool cmp(const Edge a,const Edge b){ 30 return a.dis1<b.dis1; 31 } 32 int vis[50005]; 33 void SPFA(int x,int y){ 34 int i; 35 mem.push(x);mem.push(y); 36 vis[x]=vis[y]=1; 37 while(!mem.empty()){ 38 int x=mem.front();mem.pop(); 39 vis[x]=0; 40 for(i=head[x];i!=-1;i=edge[i].next){ 41 int y=edge[i].to; 42 if(dist[y]>max(dist[x],edge[i].dis2)){ 43 dist[y]=max(dist[x],edge[i].dis2); 44 if(!vis[y]){ 45 mem.push(y); 46 vis[y]=1; 47 } 48 } 49 } 50 } 51 } 52 int main(){ 53 int i,j; 54 scanf("%d%d",&n,&m); 55 memset(head,-1,sizeof(head)); 56 for(i=1;i<=m;i++) 57 scanf("%d%d%d%d",&e[i].from,&e[i].to,&e[i].dis1,&e[i].dis2); 58 sort(e+1,e+m+1,cmp); 59 memset(dist,127/3,sizeof(dist)); 60 mem.push(1);dist[1]=0;vis[0]=1; 61 for(i=1;i<=m;i++){ 62 putin(e[i].from,e[i].to,e[i].dis1,e[i].dis2); 63 putin(e[i].to,e[i].from,e[i].dis1,e[i].dis2); 64 SPFA(e[i].from,e[i].to); 65 ans=min(ans,dist[n]+e[i].dis1); 66 } 67 if(ans==707406379)printf("-1 "); 68 else printf("%d ",ans); 69 return 0; 70 }
但是SPFA的复杂度是无法保证的,如果考场上要稳过的话就需要一个复杂度更加稳定的算法。
这题的正解是LCT,思维难度还是很高的,首先我们将边化为点,如果一条边连接x和y两个点,我们可以认为是一个点分别和x,y两点相连。这样我们就可以将权值信息放到中间那个点中。
然后还是考虑排序,先按权值a排序,从小到大加边,每次加一条边,就相当于是link一下x,再link一下y。
每次判断1和n是否联通,如果联通,就找路径上的最大值更新答案就好。
如果我们在连接的时候发现x和y是联通的,如果我们直接联通就会产生环,那么我们考虑将这个环上最大的边删掉,因为一个环上最大的边是没有存在的意义的。(当我们要经过这条最大的边的时候,我们可以从环的另外一边绕过去)
注意:我们要删掉的是这个环上最大的边,所以如果新加入的边的权值比原路径的最大值还要大,我们就没有必要加入了。(在这里被坑了好久)
1 //Never forget why you start 2 #include<iostream> 3 #include<cstdio> 4 #include<cstdlib> 5 #include<cstring> 6 #include<cmath> 7 #include<algorithm> 8 #define ll(x) lct[x].child[0] 9 #define rr(x) lct[x].child[1] 10 #define son(x,t) lct[x].child[t] 11 #define inf (2147483647) 12 using namespace std; 13 int n,m,ans=inf; 14 int read(){ 15 int ans=0,f=1;char i=getchar(); 16 while(i<'0'||i>'9'){if(i=='-')f=-1;i=getchar();} 17 while(i>='0'&&i<='9'){ans=ans*10+i-'0';i=getchar();} 18 return ans*f; 19 } 20 struct Edge{ 21 int from,to,dis1,dis2,id; 22 friend bool operator < (const Edge a,const Edge b){ 23 return a.dis1<b.dis1; 24 } 25 }e[100005]; 26 struct LCT{ 27 int child[2],fa,rev,x,mmax,size,pos; 28 bool is_root; 29 }lct[200005]; 30 void push_up(int x){ 31 lct[x].size=lct[ll(x)].size+lct[rr(x)].size+1; 32 int mmax=lct[x].x,pos=x; 33 if(lct[ll(x)].mmax>mmax)mmax=lct[ll(x)].mmax,pos=lct[ll(x)].pos; 34 if(lct[rr(x)].mmax>mmax)mmax=lct[rr(x)].mmax,pos=lct[rr(x)].pos; 35 lct[x].mmax=mmax;lct[x].pos=pos; 36 } 37 void push_rev(int x){ 38 if(!x)return; 39 swap(ll(x),rr(x)); 40 lct[x].rev^=1; 41 } 42 void push_down(int x){ 43 if(lct[x].rev){ 44 push_rev(ll(x)); 45 push_rev(rr(x)); 46 lct[x].rev^=1; 47 } 48 } 49 void push(int x){ 50 if(!lct[x].is_root)push(lct[x].fa); 51 push_down(x); 52 } 53 int getson(int x){ 54 return x==son(lct[x].fa,1); 55 } 56 void rotate(int x){ 57 if(lct[x].is_root)return; 58 int fa=lct[x].fa,fafa=lct[fa].fa,t=getson(x); 59 son(fa,t)=son(x,!t);if(son(x,!t))lct[son(x,!t)].fa=fa; 60 lct[fa].fa=x;son(x,!t)=fa; 61 lct[x].fa=fafa; 62 if(!lct[fa].is_root)son(fafa,son(fafa,1)==fa)=x; 63 else lct[x].is_root=1,lct[fa].is_root=0; 64 push_up(fa); 65 push_up(x); 66 } 67 void splay(int x){ 68 push(x); 69 for(int fa;!lct[x].is_root;rotate(x)) 70 if(!lct[fa=lct[x].fa].is_root) 71 rotate(getson(x)==getson(fa)?fa:x); 72 } 73 void access(int x){ 74 int y=0; 75 do{ 76 splay(x); 77 lct[rr(x)].is_root=1; 78 lct[rr(x)=y].is_root=0; 79 push_up(x); 80 x=lct[y=x].fa; 81 }while(x); 82 } 83 void mroot(int x){ 84 access(x); 85 splay(x); 86 push_rev(x); 87 } 88 void link(int u,int v){ 89 mroot(u); 90 lct[u].fa=v; 91 } 92 void cut(int u,int v){ 93 mroot(u); 94 access(v);splay(v); 95 lct[ll(v)].fa=lct[v].fa; 96 lct[ll(v)].is_root=1; 97 lct[v].fa=ll(v)=0; 98 push_up(v); 99 } 100 struct Fa{ 101 int fa[200005],sum; 102 void clean(){ 103 for(int i=1;i<=n+m;i++) 104 fa[i]=i; 105 sum=n+m; 106 } 107 int find(int x){ 108 if(fa[x]==x)return x; 109 else return fa[x]=find(fa[x]); 110 } 111 void merge(int x,int y){ 112 int p=find(x),q=find(y); 113 if(p!=q){ 114 fa[p]=q; 115 sum--; 116 } 117 } 118 bool judge(int x,int y){ 119 int p=find(x),q=find(y); 120 return p==q; 121 } 122 }fa; 123 int ppos[200005]; 124 int main(){ 125 int i,j; 126 n=read();m=read(); 127 fa.clean(); 128 for(i=1;i<=n;i++){ 129 lct[i].child[0]=lct[i].child[1]=lct[i].fa=0; 130 lct[i].x=lct[i].mmax=0; 131 lct[i].size=lct[i].is_root=1; 132 lct[i].pos=i; 133 } 134 for(i=1;i<=m;i++){ 135 e[i].from=read();e[i].to=read();e[i].dis1=read();e[i].id=i;e[i].dis2=lct[i+n].x=lct[i+n].mmax=read(); 136 lct[i+n].child[0]=lct[i+n].child[1]=lct[i+n].fa=0; 137 lct[i+n].size=lct[i+n].is_root=1; 138 lct[i+n].pos=i; 139 } 140 sort(e+1,e+m+1); 141 for(i=1;i<=m;i++)ppos[e[i].id]=i; 142 for(i=1;i<=m;i++){ 143 bool flag=0; 144 int u=e[i].from,v=e[i].to; 145 if(u==v)continue; 146 if(fa.judge(u,v)){ 147 mroot(u); 148 access(v); 149 splay(v); 150 if(lct[v].mmax>lct[e[i].id+n].x){ 151 flag=1; 152 int pos=lct[v].pos; 153 cut(pos,e[ppos[pos-n]].from); 154 cut(pos,e[ppos[pos-n]].to); 155 } 156 } 157 if(flag||!fa.judge(u,v)){ 158 link(e[i].id+n,u); 159 link(e[i].id+n,v); 160 fa.merge(u,e[i].id+n); 161 fa.merge(e[i].id+n,v); 162 } 163 if(fa.judge(1,n)){ 164 mroot(1); 165 access(n); 166 splay(n); 167 ans=min(ans,lct[n].mmax+e[i].dis1); 168 } 169 } 170 if(ans==inf)printf("-1 "); 171 else printf("%d ",ans); 172 return 0; 173 }