HihoCoder1139 二分·二分答案

描述

在上一回和上上回里我们知道Nettle在玩《艦これ》，Nettle在整理好舰队之后终于准备出海捞船和敌军交战了。
在这个游戏里面，海域是N个战略点(编号1..N)组成，如下图所示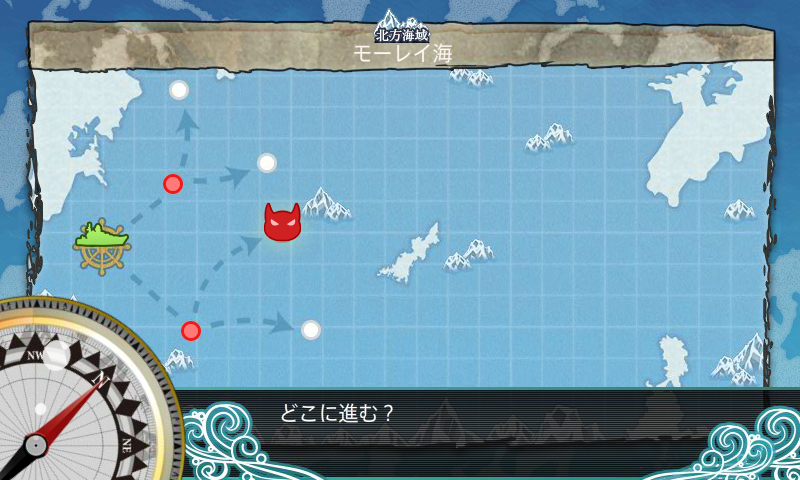

其中红色的点表示有敌人驻扎，猫头像的的点表示该地图敌军主力舰队(boss)的驻扎点，虚线表示各个战略点之间的航线(无向边)。
在游戏中要从一个战略点到相邻战略点需要满足一定的条件，即需要舰队的索敌值大于等于这两点之间航线的索敌值需求。
由于提高索敌值需要将攻击机、轰炸机换成侦察机，舰队索敌值越高，也就意味着舰队的战力越低。
另外在每一个战略点会发生一次战斗，需要消耗1/K的燃料和子弹。必须在燃料和子弹未用完的情况下进入boss点才能与boss进行战斗，所以舰队最多只能走过K条航路。
现在Nettle想要以最高的战力来进攻boss点，所以他希望能够找出一条从起始点(编号为1的点)到boss点的航路，使得舰队需要达到的索敌值最低，并且有剩余的燃料和子弹。

特别说明：两个战略点之间可能不止一条航线，两个相邻战略点之间可能不止一条航线。保证至少存在一条路径能在燃料子弹用完前到达boss点。

提示：你在找什么？

输入

第1行：4个整数N,M,K,T。N表示战略点数量，M表示航线数量，K表示最多能经过的航路，T表示boss点编号, 1≤N,K≤10,000, N≤M≤100,000
第2..M+1行：3个整数u,v,w，表示战略点u,v之间存在航路，w表示该航路需求的索敌值，1≤w≤1,000,000。

输出

第1行：一个整数，表示舰队需要的最小索敌值。

样例输入

5 6 2 5
1 2 3
1 3 2
1 4 4
2 5 2
3 5 5
4 5 3

样例输出

3

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=200000;
int vis[maxn],dis[maxn];
int Laxt[maxn],Next[maxn],To[maxn],cnt,cost[maxn];
int q[2000000],head,tail,Mid;
void add(int u,int v,int c)
{
    Next[++cnt]=Laxt[u];
    Laxt[u]=cnt;
    To[cnt]=v;
    cost[cnt]=c;
}
void dfs()
{
     while(head<tail){
            int u=q[++head];
            for(int i=Laxt[u];i;i=Next[i]){
                if(cost[i]>Mid) continue;
                int v=To[i];
                if(dis[v]>dis[u]+1){
                     dis[v]=dis[u]+1;
                     q[++tail]=v;
                }
            }
     }
}
int main()
{
    int n,m,k,t,i,c,u,v;
    scanf("%d%d%d%d",&n,&m,&k,&t);
    for(i=1;i<=m;i++){
        scanf("%d%d%d",&u,&v,&c);
        add(u,v,c);
        add(v,u,c);
    }
    int L=1,R=1000000;
    while(L<R){
        Mid=(L+R)/2;tail=head=0;q[++tail]=1;
        for(i=2;i<=n;i++) dis[i]=1000000000;    dis[1]=0;
        dfs();
        if(dis[t]<=k) R=Mid;
        else L=Mid+1;
    }
    printf("%d
",L);
    return 0;
}