【整理】关于缩点的三种题型

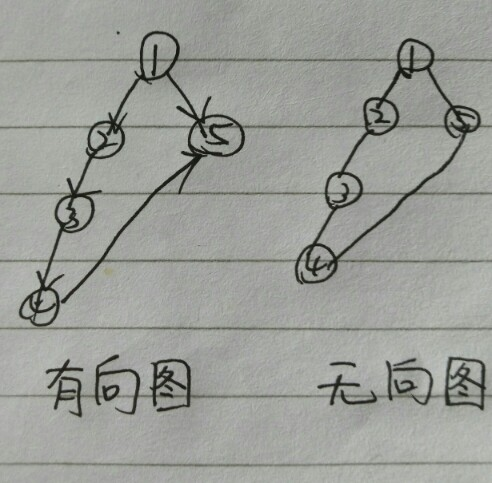
一：有向图：dfs中，不需要记录pre，但是要instack标记，从而过滤‘横边’，如4-->5；

         

void dfs(int u)
{
    instk[u]=1;
    q[++head]=u;
    dfn[u]=low[u]=++times;
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(!dfn[v]) {
            dfs(v);
            low[u]=min(low[u],low[v]);
        }
        else if(instk[v])low[u]=min(low[u],dfn[v]);//无向图与有向图的区别
    }
    if(dfn[u]==low[u]){
        scc_cnt++;
        while(true){
             int x=q[head--];
             scc[x]=scc_cnt;
             V[scc_cnt]+=w[x];
             instk[x]=0;
             if(x==u) break;
        }     
    }
}

二：无向图：dfs中需要记录pre，避免回边；有时还要考虑重边，如HDU4612；不需要instack标记。

          根据题意分为一下两种情况：

                  点的双连通存桥（边），每访问一条边操作一次。 

                 边的双连通存割点（点），访问完所有边后操作。

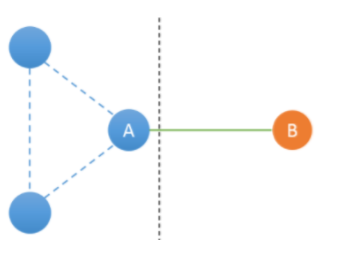
∂，边双连通算法：注意：dfn[u]==low[u]的时候并不是说u就是割点，还有可能是单个点。如图，A和B都满足（B为根），但是只有A是割点。

 dfn[u]==low[u]的意义是：

           因为low[u] == dfn[u]，对(parent[u],u)来说有dfn[u] > dfn[ parent[u] ]，因此low[u] > dfn[ parent[u]

           所以(parent[u],u)一定是一个桥，那么此时栈内在u之前入栈的点和u被该桥分割       

           则u和之后入栈的节点属于同一个组
  
           将从u到栈顶所有的元素标记为一个组，并弹出这些元素。

            

void dfs(int u,int pre)
{
    q[++head]=u;
    dfn[u]=low[u]=++times;
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(pre==v) continue;
        if(!dfn[v]){
            dfs(v,u);
            low[u]=min(low[u],low[v]);
        }
        else low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u]){
        scc_cnt++;   
        while(true){ 
            int v=q[head--];
            G[scc_cnt].push_back(v);
            scc[v]=scc_cnt;
            if(v==u) break;
        }
    }
}

β,点双连通算法：如果只是求点连通块的数量，只需要求除割点数量即可：ans=割点+1；但是要对块进行具体操作时，得记录边。

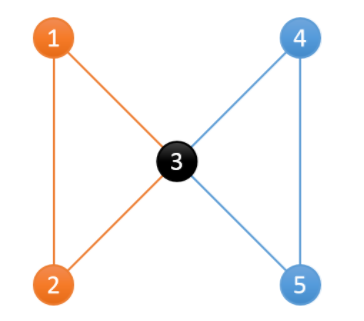
γ,二者区别：点双连通分量一定是边双连通分量（除两点一线的特殊情况），反之不一定，最经典的例子：

它是边双连通，但不是点双连通，断点就是3.

δ,不一定：

             上面说到dfn[u]==low[u]时u不一定是割点。

             low[u]==low[v]时，u和v也不一定在一个连通组里。

 求割点的代码：  

       

int dfs(int u,int pre)
{
    int son=0;
    dfn[u]=low[u]=++times;
    for(int i=Laxt[u];i;i=Next[i]){
        if(To[i]==pre) 
               continue;//不然自环了 
        if(!dfn[To[i]]){
            son++;
            dfs(To[i],u);
            low[u]=min(low[u],low[To[i]]);
            if(dfn[u]<low[To[i]]){//割边 
                s[++cut_num].x=min(u,To[i]);
                s[cut_num].y=max(u,To[i]);
            }
            if(u!=pre&&dfn[u]<=low[To[i]]){//非根割点 
                NUll=false;
                node[u]=1;
            }
        }
        else low[u]=min(low[u],dfn[To[i]]);
    }
    if(u==pre&&son>1) {//根割点 
         node[u]=1;
         NUll=false;
    }
}

求连通分量，可重新建树，代码：

         

void rebuild()
{
    for(int i=1;i<=n;i++){
        for(int j=Laxt[i];j;j=Next[j]){
            if(scc[i]!=scc[To[j]]){
                G[scc[i]].push_back(scc[To[j]]);
            }
        }
    }
}