Codeforces Round #351 (VK Cup 2016 Round 3, Div. 2 Edition) C （用map 超时）

C. Bear and Colors

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Bear Limak has n colored balls, arranged in one long row. Balls are numbered 1 through n, from left to right. There are n possible colors, also numbered 1 through n. The i-th ball has color ti.

For a fixed interval (set of consecutive elements) of balls we can define a dominant color. It's a color occurring the biggest number of times in the interval. In case of a tie between some colors, the one with the smallest number (index) is chosen as dominant.

There are 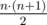 non-empty intervals in total. For each color, your task is to count the number of intervals in which this color is dominant.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 5000) — the number of balls.

The second line contains n integers t1, t2, ..., tn (1 ≤ ti ≤ n) where ti is the color of the i-th ball.

Output

Print n integers. The i-th of them should be equal to the number of intervals where i is a dominant color.

Examples

input

4
1 2 1 2

output

7 3 0 0 

input

3
1 1 1

output

6 0 0 

Note

In the first sample, color 2 is dominant in three intervals:

• An interval [2, 2] contains one ball. This ball's color is 2 so it's clearly a dominant color.
• An interval [4, 4] contains one ball, with color 2 again.
• An interval [2, 4] contains two balls of color 2 and one ball of color 1.

There are 7 more intervals and color 1 is dominant in all of them.

 题意： 给你n个数 共n*（n+1）/2个区间   求各个区间的众数作为标记数   若有多个众数 记录最小的数作为标记数  输出每个数 作为多少个区间的标记数

 题解： 暴力处理  记录各个区间的标记数。

 吃了 STL 的亏 用map 超时了 xjb用  用数组存就是 ！！！！！

#include<bits/stdc++.h>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<stack>
#include<map>
#define ll __int64
#define pi acos(-1.0)
using namespace std;
int n;
int mp[5005];
int mpp[5005];
int a[5005];
int main()
{
 //mp.clear();
 scanf("%d",&n);
 for(int i=1;i<=n;i++)
  {
    scanf("%d",&a[i]);
  }
 for(int i=1;i<=n;i++)
 {
  int maxc=-1;
  int minx=5001;
  int ans=0;
   
  for(int j=1;j<=n;j++)
   mpp[j]=0;
  for(int j=i;j<=n;j++)
  {
   mpp[a[j]]++;
   if(maxc==mpp[a[j]])
     {
       ans=min(ans,a[j]);
     }
   if(maxc<mpp[a[j]])
   {
    maxc=mpp[a[j]];
    ans=a[j]; 
   }
       mp[ans]++;
  }  
 }
 cout<<mp[1];
 for(int i=2;i<=n;i++)
 printf(" %d",mp[i]);
 cout<<endl;
 return 0;
}