1、首先确定数据分析目标——薪酬受哪些因素影响
确定变量:
因变量:薪资
自变量:(定性)-- 公司类别、公司规模、地区、行业类别、学历要求、软件要求、
(定量)-- 经验要求(数值型)
分析目标:建立因变量和自变量的多元线性回归模型,估计模型系数,检验系数显著性,确定自变量是否对因变量有影响。并实现自变量新值带入实现模型预测。
2、数据预处理。
(整理数据,使其成为可以直接建模分析的数据格式),首先看下数据结构。
1) 读数据 数据量大时不建议用xlsx包,比较慢
library(xlsx)
jobInfo2 = read.xlsx('jobinfo.xlsx',1,encoding = 'UTF-8')
str(jobInfo2) # 查看数据结构
head(jobInfo2)
2)library(readxl)
jobInfo = read_excel('jobinfo.xlsx')
str(jobInfo) # 查看数据结构
# head()函数好像没有,查看前5行
options(scipen = 200) # 去除科学计数法
jobInfo = read_excel('jobinfo.xlsx')
str(jobInfo) # 查看数据结构
1)最低薪资和最高薪资因变量转换为数值型
jobInfo$最低薪资 = as.numeric(jobInfo$最低薪资) jobInfo$最高薪资 = as.numeric(jobInfo$最高薪资) jobInfo$平均薪资 = (jobInfo$最低薪资+jobInfo$最高薪资)/2
2) 地区处理,分北上深和非北上深
loc = which(jobInfo$地区 %in% c("北京","上海","深圳"))
loc_other = which(!jobInfo$地区 %in% c("北京","上海","深圳"))
jobInfo$地区[loc] = 1
jobInfo$地区[loc_other] = 0
jobInfo$地区 = as.numeric(jobInfo$地区)
3) 处理公司规模、学历,转化为因子变量。便于画图
jobInfo$公司规模 = factor(jobInfo$公司规模,levels = c("少于50人", "50-150人", "150-500人", "500-1000人", "1000-5000人", "5000-10000人", "10000人以上"))
levels(jobInfo$公司规模)[c(2, 3)] = c("50-500人","50-500人")
jobInfo$学历 = factor(jobInfo$学历,levels = c("中专", "高中", "大专", "无", "本科", "硕士", "博士"))
4)匹配公司需求掌握的工具
分析工具包含:"R", "SPSS", "Excel", "Python", "MATLAB", "Java", "SQL", "SAS", "Stata", "EViews", "Spark", "Hadoop"
software = as.data.frame(matrix(0,nrow = length(jobInfo$描述),ncol = 12)) # 生成*行*列的数据框
colnames(software) = c("R", "SPSS", "Excel", "Python", "MATLAB", "Java", "SQL", "SAS", "Stata", "EViews", "Spark", "Hadoop")
mixseg = worker()
for (i in 1:length(jobInfo$描述)) {
subData = as.character(jobInfo$描述[i])
fenci = mixseg[subData]
R.identify = ("R" %in% fenci) | ("r" %in% fenci)
SPSS.identify = ("spss" %in% fenci) | ("Spss" %in% fenci) | ("SPSS" %in% fenci)
Excel.identify = ("excel" %in% fenci) | ("EXCEL" %in% fenci) | ("Excel" %in% fenci)
Python.identify = ("Python" %in% fenci) | ("python" %in% fenci) | ("PYTHON" %in% fenci)
MATLAB.identify = ("matlab" %in% fenci) | ("Matlab" %in% fenci) | ("MATLAB" %in% fenci)
Java.identify = ("java" %in% fenci) | ("JAVA" %in% fenci) | ("Java" %in% fenci)
SQL.identify = ("SQL" %in% fenci) | ("Sql" %in% fenci) | ("sql" %in% fenci)
SAS.identify = ("SAS" %in% fenci) | ("Sas" %in% fenci) | ("sas" %in% fenci)
Stata.identify = ("STATA" %in% fenci) | ("Stata" %in% fenci) | ("stata" %in% fenci)
EViews.identify = ("EViews" %in% fenci) | ("EVIEWS" %in% fenci) | ("Eviews" %in% fenci) | ("eviews" %in% fenci)
Spark.identify = ("Spark" %in% fenci) | ("SPARK" %in% fenci) | ("spark" %in% fenci)
Hadoop.identify = ("HADOOP" %in% fenci) | ("Hadoop" %in% fenci) | ("hadoop" %in% fenci)
if (R.identify) software$R[i] = 1
if (SPSS.identify) software$SPSS[i] = 1
if (Excel.identify) software$Excel[i] = 1
if (Python.identify) software$Python[i] = 1
if (MATLAB.identify) software$MATLAB[i] = 1
if (Java.identify) software$Java[i] = 1
if (SQL.identify) software$SQL[i] = 1
if (SAS.identify) software$SAS[i] = 1
if (Stata.identify) software$Stata[i] = 1
if (EViews.identify) software$EViews[i] = 1
if (Spark.identify) software$Spark[i] = 1
if (Hadoop.identify) software$Hadoop[i] = 1
}
jobInfo.new = cbind(jobInfo$平均薪资,software)
colnames(jobInfo.new) = c("平均薪资",colnames(software))
# 合并其他列
jobInfo.new$地区 = jobInfo$地区
jobInfo.new$公司类别 = jobInfo$公司类别
jobInfo.new$公司规模 = jobInfo$公司规模
jobInfo.new$学历 = jobInfo$学历
jobInfo.new$经验要求 = jobInfo$经验
jobInfo.new$行业类别 = jobInfo$行业类别
table(jobInfo.new$公司类别) # 分析公司类别中观测值少的予以删除
jobInfo.new = jobInfo.new[-which(jobInfo.new$公司类别 %in% c("事业单位","非营利机构")),]
colnames(jobInfo.new) = c('aveSalary' , colnames(jobInfo.new[2:13]),"area", "compVar", "compScale", "academic", "exp", "induCate")
# 保存数据集
write.csv(jobInfo.new, file= '数据分析岗位招聘.csv', row.names = F)
3、数据可视化
1) 描述性分析 因变量直方图薪资分布情况
hist(dat0$aveSalary, xlab = "平均薪资(元/月)",ylab = "频数",main = "", col = 'dodgerblue',xlim = c(1500,11000),
breaks = seq(0,500000,by=1500))
summary(dat0$aveSalary)
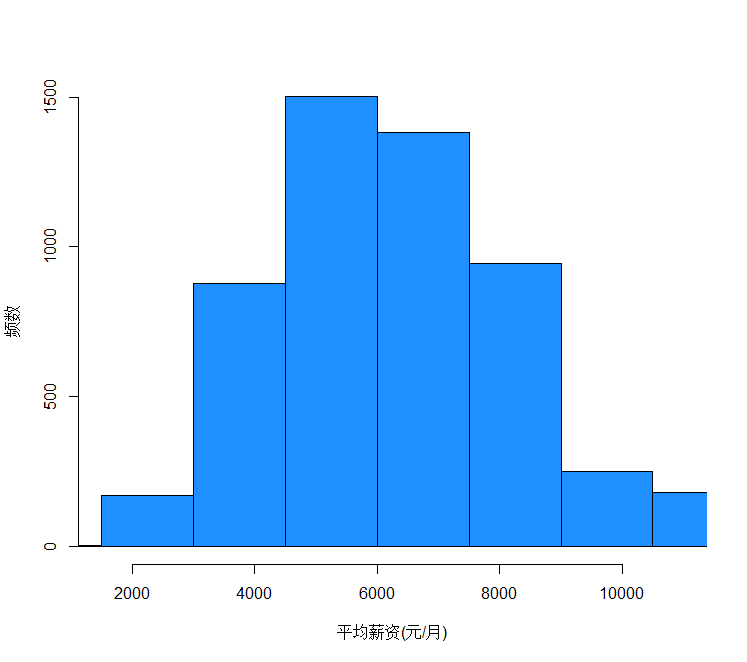
2)平均薪资经验要求---箱线图
dat0$exp_level = cut(dat0$exp, breaks = c(-0.01,3.99,6,max(dat0$exp)))
dat0$exp_level = factor(dat0$exp_level, levels = levels(dat0$exp_level),
labels = c("经验:0-3年", "经验:4-6年", "经验:>6年"))
boxplot(aveSalary~exp_level,data = dat0,col = 'dodgerblue',ylab = "平均薪资(元/月)",ylim = c(0,45000))
summary(lm(aveSalary~exp_level,data = dat0))
table(dat0$exp_level)


3) 平均薪资~学历 箱线图
dat0$academic = factor(dat0$academic, levels = c("无", "中专", "高中", "大专", "本科", "硕士", "博士"))
dat0$compVar = factor(dat0$compVar, levels = c("民营公司", "创业公司", "国企", "合资", "上市公司", "外资"))
boxplot(aveSalary~academic,data = dat0,col='dodgerblue',ylab = '平均薪资(元/月)',ylim = c(0,45000))
summary(lm(aveSalary~academic, data = dat0))
table(dat0$academic)

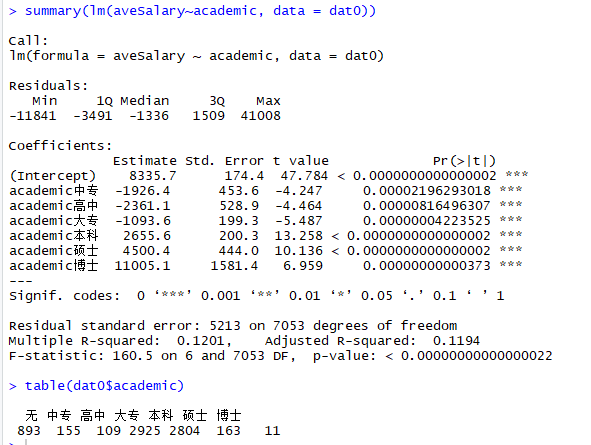
4、建立回归模型
lm1 = lm(aveSalary~.,data = dat0) summary(lm1) lm2 = lm(aveSalary~.-induCate-exp_level,data = dat0) summary(lm2) par(mfrow = c(2,2)) # 回归诊断 plot(lm2,which = c(1:4))
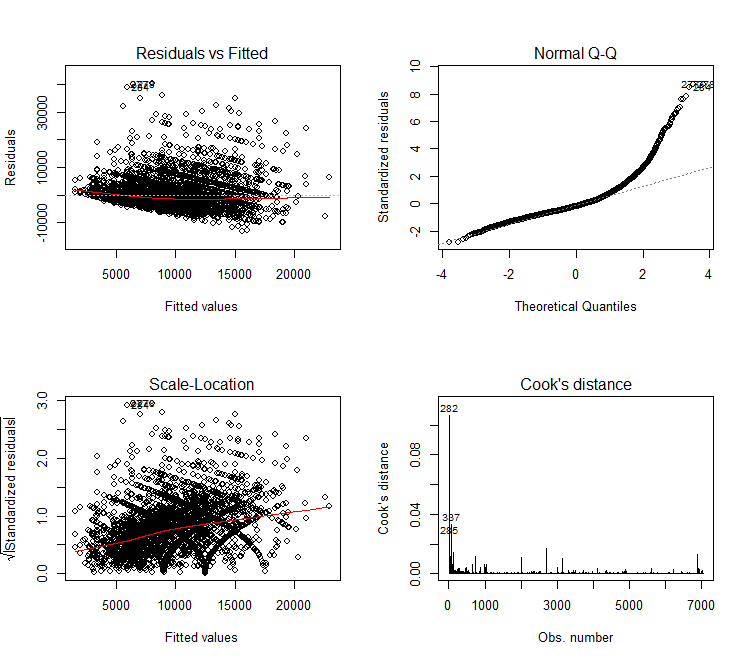
QQ图看出结果存在非正态性,线性非45°,对因变量取对数继续分析。
# install.packages('rms')
library(rms)
vif(lm2) # 计算VIF,>5代表共线性较大,(对其他自变量的回归的R^2>80%)
# 去除共线性因素,合并VIF较大的几项与基准组合并为一项
# dat0$compVar = as.character(dat0$compVar)
# dat0[which(dat0$compVar %in% c("合资", "外资", "民营公司", "创业公司")),"compVar"] = "其他" # 将合资,外资,民营公司、创业公司转换为其他
# dat0$compVar = factor(dat0$compVar,levels = c("其他","国企","上市公司"))
#
# lm3 = lm(aveSalary~.-induCate-exp_level,data = dat0)
# summary(lm3)
# vif(lm3)
# 去除非正态性影响,对数线性模型
lm4 = lm(log(aveSalary)~.-induCate-exp_level,data = dat0)
summary(lm4)
par(mfrow = c(2,2))
plot(lm4,which = c(1:4))
# # 库克异常点处理
# cook = cooks.distance(lm4)
# cook = sort(cook,decreasing = T)
# cook_point = names(cook)[1]
# cook_delete = which(rownames(dat0) %in% cook_point)
# dat0 = dat0[-cook_delete,]
#
# # 检查
# lmTest = lm(log(aveSalary)~.-induCate-exp_level,data = dat0)
# par(mfrow = c(2,2))
# plot(lmTest,which = c(1,4))
改善后效果图:
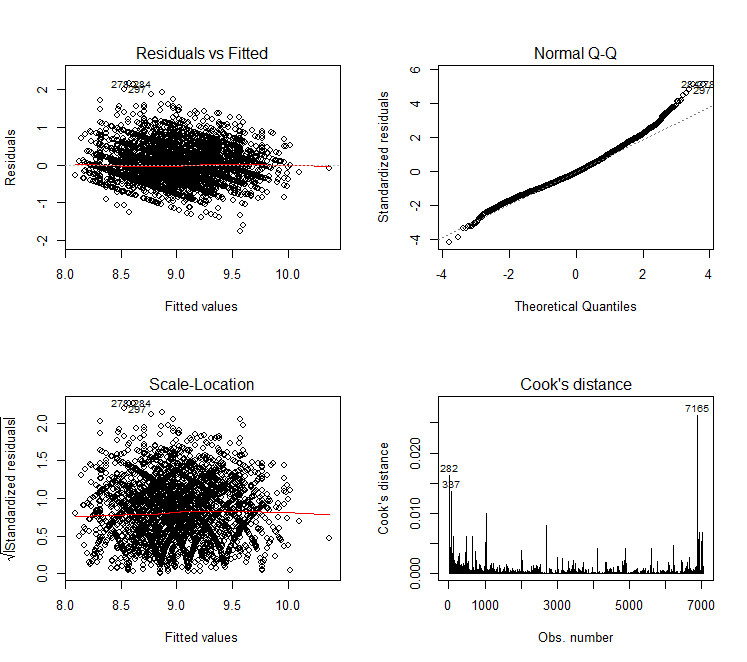
最终模型预测:
- 假定确定交互项公司规模和地区的乘积为增加的影响因子compScale*area,(过程推导step函数判别,AIC值越小越好(负数也一样判断))
- 逐步回归分析是以AIC信息统计量为准则,通过选择最小的AIC信息统计量,来达到删除或增加变量的目的。
dat1 = dat0[1:18] lm0 = lm(log(aveSalary)~.+compScale*area,data = dat1) summary(step(lm0)) # 结果得出初始有交互项compScale*area的模型最好
从AIC值可以看出来初始有交互项compScale*area的模型最好。
Start: AIC=-12289.46
log(aveSalary) ~ R + SPSS + Excel + Python + MATLAB + Java +
SQL + SAS + Stata + EViews + Spark + Hadoop + area + compVar +
compScale + academic + exp + compScale * area
Df Sum of Sq RSS AIC
- area:compScale 5 1.338 1227.1 -12292
- EViews 1 0.000 1225.7 -12292
- Spark 1 0.037 1225.8 -12291
- Stata 1 0.165 1225.9 -12290
- SPSS 1 0.237 1226.0 -12290
- MATLAB 1 0.272 1226.0 -12290
<none> 1225.7 -12290
- Java 1 0.662 1226.4 -12288
- SAS 1 0.762 1226.5 -12287
- R 1 0.872 1226.6 -12286
- Python 1 1.555 1227.3 -12282
- compVar 5 3.479 1229.2 -12280
- Hadoop 1 6.249 1232.0 -12256
- SQL 1 9.494 1235.2 -12237
- Excel 1 22.307 1248.0 -12164
- academic 6 114.286 1340.0 -11672
- exp 1 214.853 1440.6 -11151
Step: AIC=-12291.76
log(aveSalary) ~ R + SPSS + Excel + Python + MATLAB + Java +
SQL + SAS + Stata + EViews + Spark + Hadoop + area + compVar +
compScale + academic + exp
Df Sum of Sq RSS AIC
- EViews 1 0.000 1227.1 -12294
- compScale 5 1.416 1228.5 -12294
- Spark 1 0.038 1227.1 -12294
- Stata 1 0.166 1227.2 -12293
- SPSS 1 0.245 1227.3 -12292
- MATLAB 1 0.256 1227.3 -12292
<none> 1227.1 -12292
- Java 1 0.652 1227.7 -12290
- SAS 1 0.739 1227.8 -12290
- R 1 0.856 1227.9 -12289
- Python 1 1.569 1228.6 -12285
- compVar 5 3.531 1230.6 -12282
- Hadoop 1 6.216 1233.3 -12258
- SQL 1 9.359 1236.4 -12240
- Excel 1 22.587 1249.7 -12165
- academic 6 113.393 1340.5 -11680
- area 1 149.888 1377.0 -11480
- exp 1 215.650 1442.7 -11151
Step: AIC=-12293.76
log(aveSalary) ~ R + SPSS + Excel + Python + MATLAB + Java +
SQL + SAS + Stata + Spark + Hadoop + area + compVar + compScale +
academic + exp
Df Sum of Sq RSS AIC
- compScale 5 1.417 1228.5 -12296
- Spark 1 0.037 1227.1 -12296
- Stata 1 0.167 1227.2 -12295
- SPSS 1 0.246 1227.3 -12294
- MATLAB 1 0.257 1227.3 -12294
<none> 1227.1 -12294
- Java 1 0.653 1227.7 -12292
- SAS 1 0.739 1227.8 -12292
- R 1 0.861 1227.9 -12291
- Python 1 1.569 1228.6 -12287
- compVar 5 3.531 1230.6 -12284
- Hadoop 1 6.216 1233.3 -12260
- SQL 1 9.360 1236.4 -12242
- Excel 1 22.597 1249.7 -12167
- academic 6 113.394 1340.5 -11682
- area 1 149.898 1377.0 -11482
- exp 1 215.652 1442.7 -11153
Step: AIC=-12295.61
log(aveSalary) ~ R + SPSS + Excel + Python + MATLAB + Java +
SQL + SAS + Stata + Spark + Hadoop + area + compVar + academic +
exp
Df Sum of Sq RSS AIC
- Spark 1 0.036 1228.5 -12297
- Stata 1 0.170 1228.7 -12297
- SPSS 1 0.261 1228.7 -12296
- MATLAB 1 0.298 1228.8 -12296
<none> 1228.5 -12296
- Java 1 0.633 1229.1 -12294
- SAS 1 0.752 1229.2 -12293
- R 1 0.878 1229.3 -12293
- Python 1 1.547 1230.0 -12289
- compVar 5 3.779 1232.3 -12284
- Hadoop 1 6.288 1234.8 -12262
- SQL 1 9.517 1238.0 -12243
- Excel 1 22.306 1250.8 -12171
- academic 6 113.717 1342.2 -11683
- area 1 152.798 1381.3 -11470
- exp 1 217.467 1445.9 -11147
Step: AIC=-12297.41
log(aveSalary) ~ R + SPSS + Excel + Python + MATLAB + Java +
SQL + SAS + Stata + Hadoop + area + compVar + academic +
exp
Df Sum of Sq RSS AIC
- Stata 1 0.166 1228.7 -12298
- SPSS 1 0.256 1228.8 -12298
- MATLAB 1 0.297 1228.8 -12298
<none> 1228.5 -12297
- Java 1 0.606 1229.1 -12296
- SAS 1 0.761 1229.3 -12295
- R 1 0.888 1229.4 -12294
- Python 1 1.520 1230.0 -12291
- compVar 5 3.779 1232.3 -12286
- Hadoop 1 8.237 1236.8 -12252
- SQL 1 9.549 1238.1 -12245
- Excel 1 22.302 1250.8 -12172
- academic 6 113.684 1342.2 -11685
- area 1 153.022 1381.5 -11471
- exp 1 217.431 1445.9 -11149
Step: AIC=-12298.46
log(aveSalary) ~ R + SPSS + Excel + Python + MATLAB + Java +
SQL + SAS + Hadoop + area + compVar + academic + exp
Df Sum of Sq RSS AIC
- SPSS 1 0.258 1228.9 -12299
<none> 1228.7 -12298
- MATLAB 1 0.405 1229.1 -12298
- Java 1 0.615 1229.3 -12297
- SAS 1 0.715 1229.4 -12296
- R 1 0.859 1229.5 -12296
- Python 1 1.504 1230.2 -12292
- compVar 5 3.781 1232.5 -12287
- Hadoop 1 8.212 1236.9 -12253
- SQL 1 9.817 1238.5 -12244
- Excel 1 22.319 1251.0 -12173
- academic 6 113.730 1342.4 -11686
- area 1 152.949 1381.6 -11472
- exp 1 217.584 1446.3 -11149
Step: AIC=-12298.97
log(aveSalary) ~ R + Excel + Python + MATLAB + Java + SQL + SAS +
Hadoop + area + compVar + academic + exp
Df Sum of Sq RSS AIC
<none> 1228.9 -12299
- MATLAB 1 0.385 1229.3 -12299
- Java 1 0.587 1229.5 -12298
- R 1 1.003 1229.9 -12295
- Python 1 1.495 1230.4 -12292
- SAS 1 1.854 1230.8 -12290
- compVar 5 3.763 1232.7 -12287
- Hadoop 1 8.280 1237.2 -12254
- SQL 1 10.189 1239.1 -12243
- Excel 1 22.096 1251.0 -12175
- academic 6 114.599 1343.5 -11682
- area 1 153.067 1382.0 -11472
- exp 1 217.601 1446.5 -11150
Call:
lm(formula = log(aveSalary) ~ R + Excel + Python + MATLAB + Java +
SQL + SAS + Hadoop + area + compVar + academic + exp, data = dat1)
Residuals:
Min 1Q Median 3Q Max
-1.72378 -0.28570 -0.04861 0.25334 2.14908
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.456762 0.017967 470.678 < 0.0000000000000002 ***
R 0.065522 0.027340 2.397 0.016576 *
Excel -0.143574 0.012763 -11.249 < 0.0000000000000002 ***
Python 0.085599 0.029258 2.926 0.003448 **
MATLAB -0.056898 0.038301 -1.486 0.137439
Java 0.058288 0.031793 1.833 0.066791 .
SQL 0.145021 0.018985 7.639 0.0000000000000248 ***
SAS 0.078317 0.024033 3.259 0.001125 **
Hadoop 0.229420 0.033317 6.886 0.0000000000062357 ***
area 0.394826 0.013335 29.607 < 0.0000000000000002 ***
compVar创业公司 0.082482 0.044609 1.849 0.064501 .
compVar国企 -0.026972 0.027142 -0.994 0.320391
compVar合资 0.056369 0.016646 3.386 0.000712 ***
compVar上市公司 0.058643 0.022498 2.607 0.009165 **
compVar外资 0.005431 0.016148 0.336 0.736654
academic中专 -0.227767 0.036399 -6.257 0.0000000004143217 ***
academic高中 -0.248540 0.042443 -5.856 0.0000000049575319 ***
academic大专 -0.149227 0.016084 -9.278 < 0.0000000000000002 ***
academic本科 0.108561 0.016581 6.547 0.0000000000627649 ***
academic硕士 0.269012 0.036317 7.407 0.0000000000001438 ***
academic博士 0.807996 0.127023 6.361 0.0000000002129521 ***
exp 0.099921 0.002831 35.301 < 0.0000000000000002 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4179 on 7038 degrees of freedom
Multiple R-squared: 0.3778, Adjusted R-squared: 0.3759
F-statistic: 203.5 on 21 and 7038 DF, p-value: < 0.00000000000000022
5、模型预测
有3个求职者特点如下,预测其薪资。
1)会用r和python,本科毕业,无工作经验,公司位于上海,规模87人,上市公司。
2)会用r,java,sas和python,博士毕业,7年工作经验,公司位于北京,中小型公司(规模150-500人),创业公司。
3)没有学历、微弱的国企工作经验、不会任何统计软件。
new_data1 = matrix(c(1,0,0,1,0,0,0,0,0,0,0,0,1,"上市公司","50-500人","本科",0),1,17)
new_data2 = matrix(c(1,0,0,1,0,1,0,1,0,0,0,0,1,"创业公司","50-500人","博士",7),1,17)
new_data3 = matrix(c(0,0,0,0,0,0,0,0,0,0,0,0,0,"国企","少于50人","无",0),1,17)
new_data1 = as.data.frame(new_data1)
new_data2 = as.data.frame(new_data2)
new_data3 = as.data.frame(new_data3)
colnames(new_data1) = names(dat0)[2:18]
colnames(new_data2) = names(dat0)[2:18]
colnames(new_data3) = names(dat0)[2:18]
for (j in 1:13) {
new_data1[,j] = as.numeric(as.character(new_data1[,j]))
new_data2[,j] = as.numeric(as.character(new_data2[,j]))
new_data3[,j] = as.numeric(as.character(new_data3[,j]))
}
new_data1$exp = as.numeric(as.character(new_data1$exp))
new_data2$exp = as.numeric(as.character(new_data2$exp))
new_data3$exp = as.numeric(as.character(new_data2$exp))
# 预测
exp(predict(lm0,new_data1))
exp(predict(lm0,new_data2))
exp(predict(lm0,new_data3))
实现预测Salary值:
