Pthon Matplotlib 画图

一、普通绘图

import matplotlib.pyplot as plt
import numpy as np

# 绘制普通图像
x = np.linspace(-1, 1, 50)
y1 = 2 * x + 1
y2 = x**2

plt.figure()
# 在绘制时设置lable, 逗号是必须的
l1, = plt.plot(x, y1, label = 'line')
l2, = plt.plot(x, y2, label = 'parabola', color = 'red', linewidth = 1.0, linestyle = '--')

# 设置坐标轴的取值范围
plt.xlim((-1, 1))
plt.ylim((0, 2))

# 设置坐标轴的lable
plt.xlabel('X axis')
plt.ylabel('Y axis')

# 设置x坐标轴刻度, 原来为0.25, 修改后为0.5
plt.xticks(np.linspace(-1, 1, 5))
# 设置y坐标轴刻度及标签, $$是设置字体
plt.yticks([0, 0.5], ['$minimum$', 'normal'])

# 设置legend
plt.legend(handles = [l1, l2,], labels = ['a', 'b'], loc = 'best')
plt.show()

二、自定义单峰函数

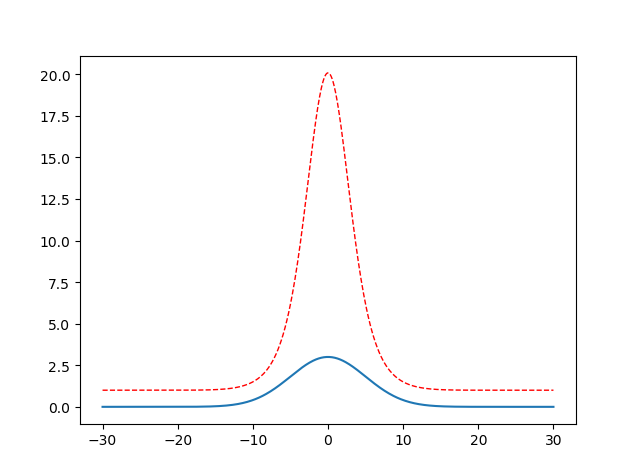
import math
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-30, 30, 500)
y = []
y2 = []
a = 3
b = 0
c = 25
for i in x :
    # 类似高斯函数，a 代表峰值， b对称轴位置，c方差
    temp = a * math.exp(-(i-b)**2 / (2 * c))
    y.append(temp) 
    #对上一个单峰函数值进行放大处理,红色虚线部分
    y2.append(math.exp(temp))

plt.figure()
l1= plt.plot(x, y, label = 'line')
l2, = plt.plot(x, y2, label = 'parabola', color = 'red', linewidth = 1.0, linestyle = '--')
plt.show()

三、画subplot子图（2 x 2 为例）

    import matplotlib.pyplot as plt
    t=np.arange(0.0,2.0,0.1)
    s=np.sin(t*np.pi)
    plt.subplot(2,2,1) #要生成两行两列，这是第一个图plt.subplot('行','列','编号')
    plt.plot(t,s,'b--')
    plt.ylabel('y1')
    plt.subplot(2,2,2) #两行两列,这是第二个图
    plt.plot(2*t,s,'r--')
    plt.ylabel('y2')
    plt.subplot(2,2,3)#两行两列,这是第三个图
    plt.plot(3*t,s,'m--')
    plt.subplot(2,2,4)#两行两列,这是第四个图
    plt.plot(4*t,s,'k--')
    plt.show()

 点图和线图

fig = plt.figure()
ax = fig.add_subplot(221, projection='3d')
ax.plot(array_normal[:,0],array_normal[:,1],array_normal[:,2])
plt.subplot(2,2,2)
plt.plot(np.arange(0,sample_len,1), signal_normal)

normal_pow = array_normal[:,2]

ax3 = fig.add_subplot(223, projection='3d')
ax3.plot(array_anomaly[:,0],array_anomaly[:,1],array_anomaly[:,2])

anomaly_pow = array_anomaly[:,2]
plt.subplot(2,2,4)
plt.scatter(np.arange(0,sample_len,1), signal_anomaly)
plt.show()

【Reference】

[1] https://www.jianshu.com/p/de223a79217a

[2] https://www.cnblogs.com/xingshansi/p/6777945.html