话说这个系列鸽了好久,之前在准备语言考试,就没管博客了,现在暑假咱们继续上路!
每当我们进行一次插入之后,整棵AVL树的平衡性就有可能发生改变,为了控制整棵树的高度,我们需要通过一系列变换(重平衡)来保证它仍满足AVL的平衡条件。我们把需要重新平衡的节点叫做 ⍺,由于任意节点最多有两个儿子,因此高度不平衡时,⍺的两颗子树高度差2。考虑一下产生不平衡会有几种情况,稍加思索就会明白——四种情况的插入:
- ⍺->left->left
- ⍺->left->right
- ⍺->right->left
- ⍺->right->right
情形1和4,2和3 分别是关于⍺的镜像对称,从理论上来讲只有两种情况,当然,从编程角度还是四种情况。
先说一些约定:
struct AvlNode; typedef struct AvlNode *Position; typedef struct AvlNode *AvlTree; struct AvlNode { int value; AvlTree lc; AvlTree rc; int Height; }; int max(int a,int b){ return a>b?a:b;}
下面先从思路角度予以说明,一段思路说清后立即给出代码实现,趁热打铁,就易于接受了。
外侧情形-单旋转
第一种情况是发生在外侧(左-左or右-右),情形1、4,这需要一次单旋转来完成。
先说“右-右”的情况,这种旋转也叫zag

这里两个灰色的方块是可能插入的节点,虚线连接表示只能取一处,g是可能发生失衡的最深的节点(因为往上的祖先也有可能发生失衡),而g就是当前发生失衡最近的节点。我们要围绕着g做一次”右-右“旋转。先说一下宏观的思路:为了使树恢复平衡,我们把p的右子树整体上移一层,并把T0下移一层,不过这样一来,实际上超出了AVL的特性要求,为此我们重新安排节点以形成一颗等价的树,如下所示:

抽象地形容就是:把树形象地看成是柔软灵活的,抓住节点p,闭上你的双眼使劲摇动它,在重力作用下p就成了新的根。BST的性质告诉我们,在原树中g<p,于是在新树中g变成了
p的左孩子,T0和p的右子树的各自隶属关系仍然不变。子树T1包含原树中介于g和p之间的的那些节点(因为原树中g<T1<p),可以将它放在新树中g的右孩子的位置上,这样所有对元素大小的要求都能得到满足了。
怎么做呢?首先用一个临时指针指向p
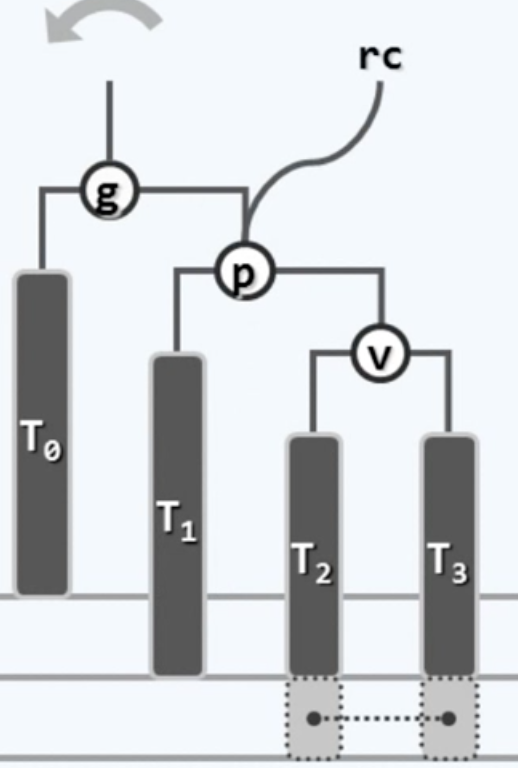
然后我们让T1成为g的右孩子,为此要这样调整:

接下来我们令g成为p的左孩子:

接下来我们要让局部子树的根由g变化为p,然后临时指针退休。
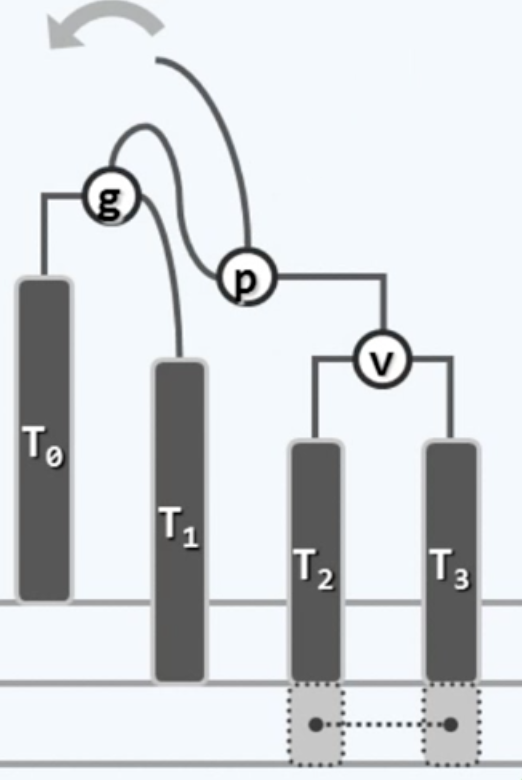
如此一来就完成了“右-右”的单旋转,整理一下就能看得更清了:
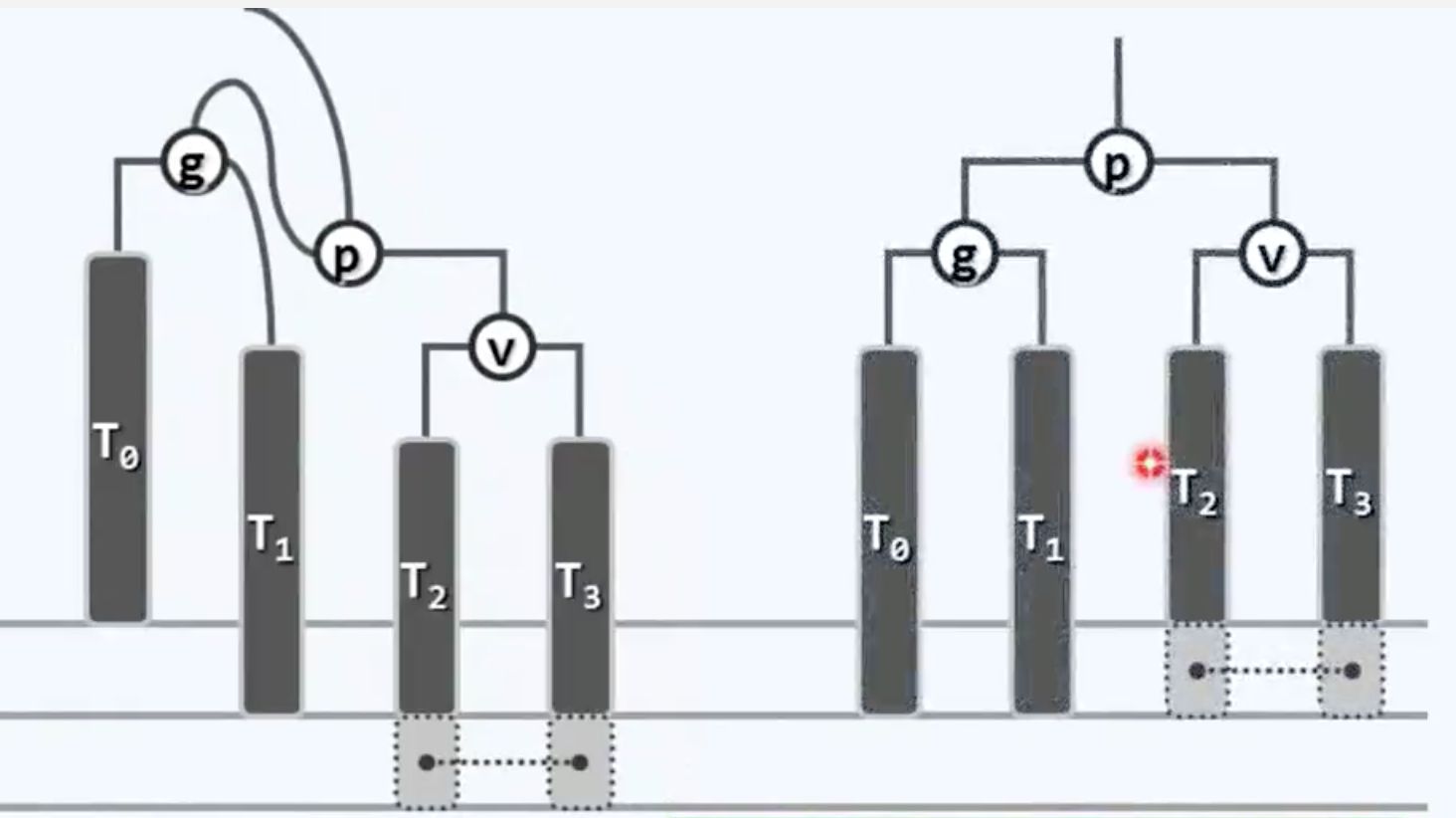
让我们把这个思路兑现为代码

/* 只有在 g 存在右孩子的情况下才被调用,在g和他的右孩子之间进行旋转操作。 最后要记得实时更新高度,返回当前的新树根 */ static Position SingleRotateWithRight( Position g ) { Position temp; temp = g->rc; g->rc = temp->lc; temp->lc = g; g->Height = max( Height( g->lc ), Height( g->rc ) ) + 1; temp->Height = max( Height( temp->rc ), g->Height ) + 1; return temp; /* New root */ }
如果在此前g以上的祖先还有发生失衡,在这个局部重平衡之后,上面的各个节点也能一并恢复平衡。因为在这里除了平衡因子外,局部子树还有一个指标:高度。留意一下我们设置的三条基准线,在插入新节点之前,原树的高度以中线为基准,对照重新平衡后的树,它的高度又回到了中间的基准线上。那这又意味着什么呢?这意义十分重大,意味着他所有祖先在计算平衡因子时所得结果,也将与插入节点前完全一样,换而言之,上面的节点也都恢复平衡,那么全树都恢复了平衡。而我们只做了一次“右-右”旋转,只涉及常数个节点,时间消耗O(1),这再好不过了。
再说“左-左”旋转,也叫zig,比如对于这个局部
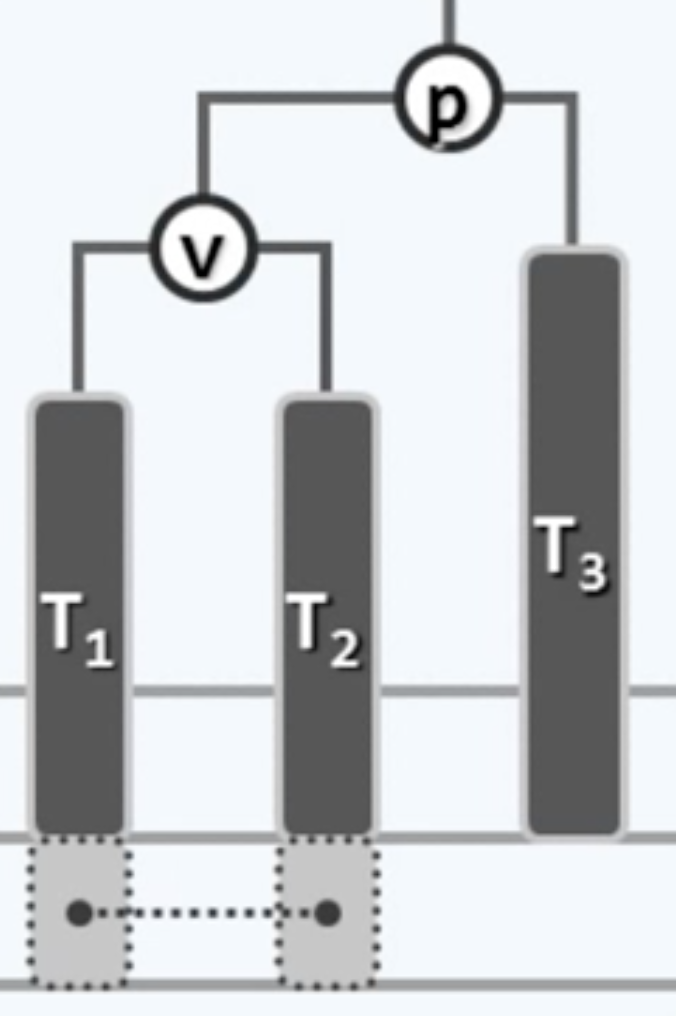
先用一个临时指针指向v
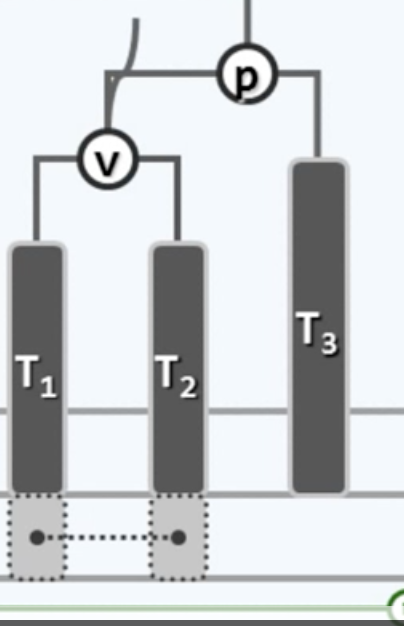
然后让T2成为p的左孩子
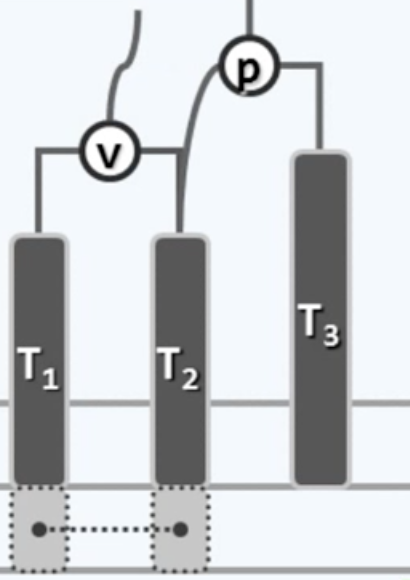
然后让p成为v的右孩子

最后把局部子树的根由p变更为v,临时指针下岗
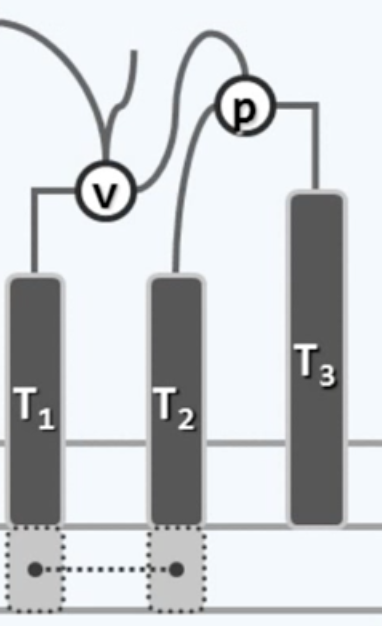
至此“左-左”旋转宣告完成,兑换为代码:

//仅当p存在左孩子时调用这个函数,更新高度并返回新的根 static Position SingleRotateWithLeft( Position p ) { Position temp; temp = p->lc; p->lc = temp->rc; temp->rc = p; p->Height = max( Height( p->lc ), Height( p->rc ) ) + 1; temp->Height = max( Height( temp->lc ), p->Height ) + 1; return temp; /* New root */ }
上面的算法有一个问题,就是解决的情况都是父子节点在朝向上是一致的,如果朝向不一致呢?单旋转就有心无力了,经过单旋转并不会降低它的深度,就需要引入第二种情况了:
内侧情形-双旋转
第二种情况是发生在内侧(左-右or右-左),这需要一次双旋转来完成,其实就是两个单旋转的组合,往往是方向相反的一组单旋转协同工作
先说右-左的情况,如下:
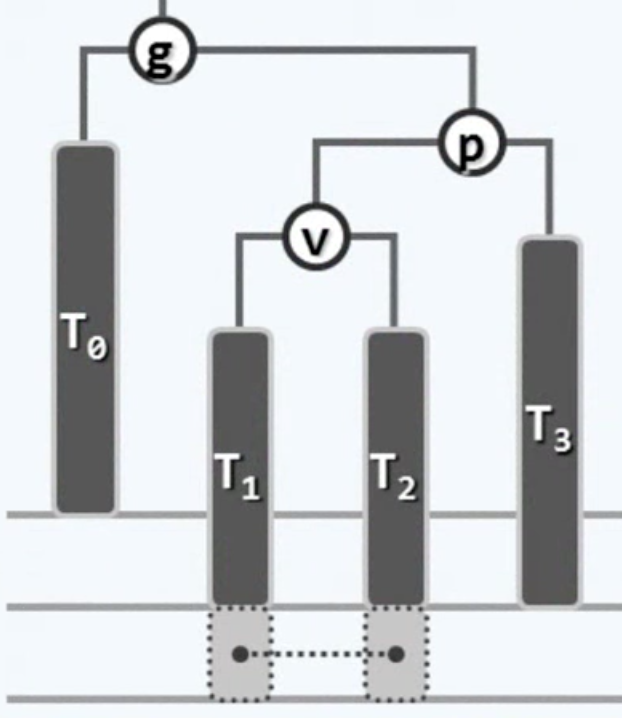
我们要抽丝剥茧地做重平衡操作,先看p-v这个局部,都朝向左边,所以首先的思路是对p执行一次顺时针的左-左的单旋转,就变成了这样:
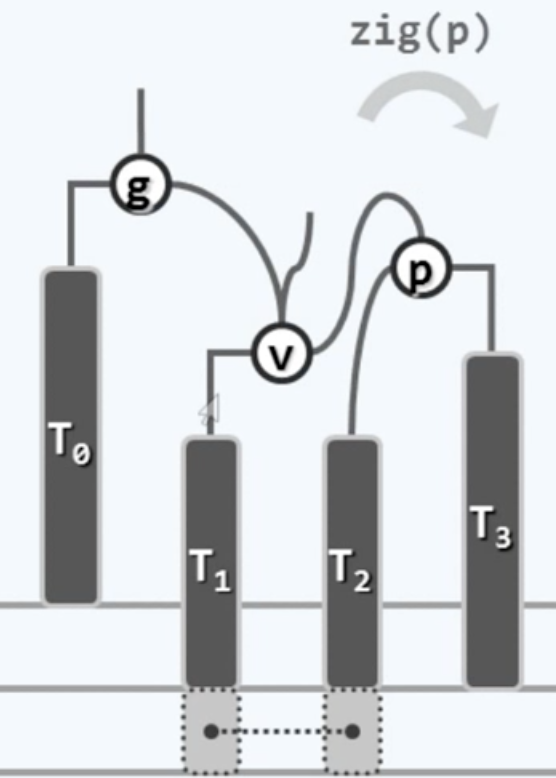
到这里,g,v,p三个节点就朝向一致了,那么显然,接下来我们要针对g做一次逆时针的zag旋转,和之前说的过程完全一样:
T1成为g的右孩子
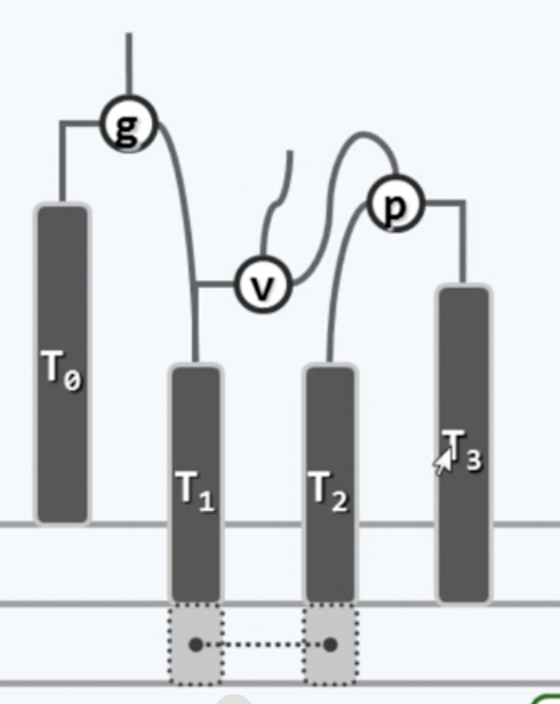
g成为v的左孩子(感觉这只蜘蛛要扑过来了2333)
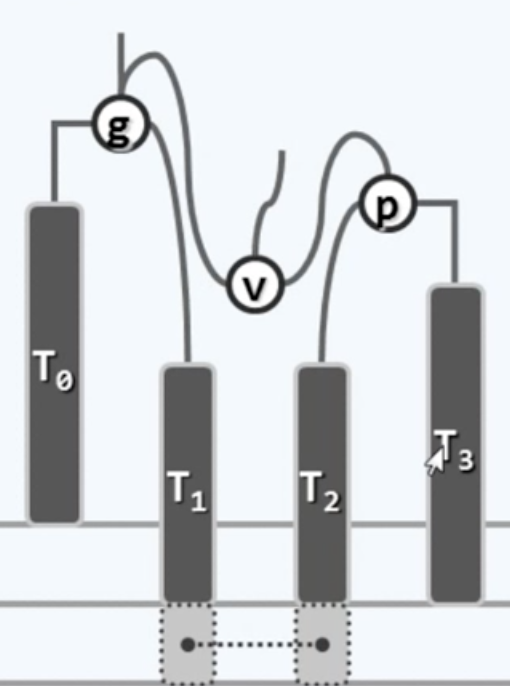
这样就完成了局部的重平衡,当然,这里再把细节展示出来是为了方便深入理解,实际写代码的时候直接调用对应单旋转操作,把g传进去就行了。为了清晰看出效果,做一下整理:
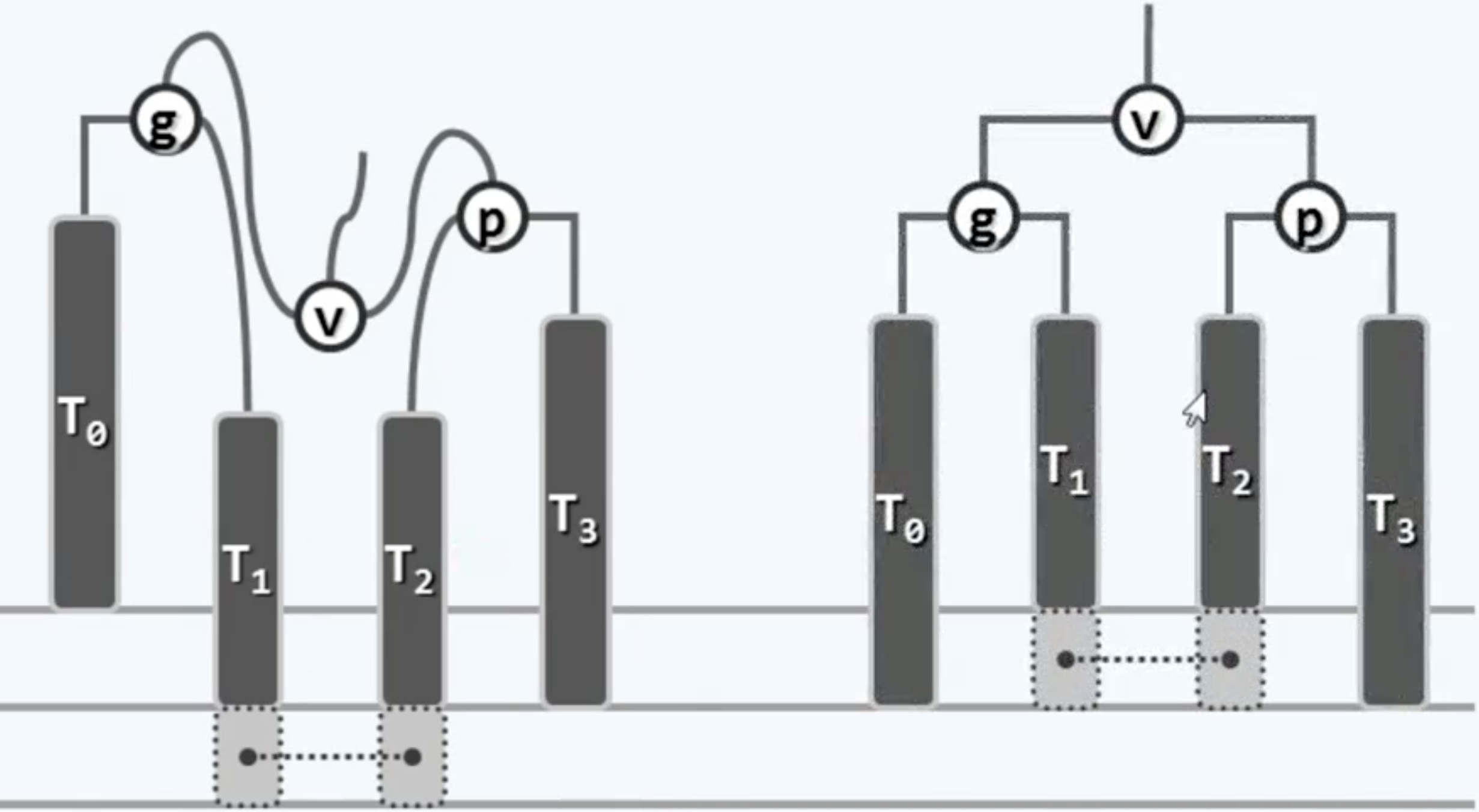
的确已经恢复平衡,以上可能失衡的祖先也会一并回复平衡。

// This function can be called only if g has a right // child and g's right child has a left child // Do the right-left double rotation // Update heights, then return new root static Position DoubleRotateWithRight( Position g ) { // Rotate between p and v, p means g->rc g->rc = SingleRotateWithLeft( g->rc ); // Rotate between g and p return SingleRotateWithRight( g ); }
下面再说左-右旋转的情况:

为了重新平衡,就不能让k3继续是根了,不然高度永远降不下来。那么唯一的选择就是让k2作为新的根,如此一来根据BST的性质,我们必须把k1放在左孩子的位置上,k3放在右孩子的位置上。具体的做法是对k1,k2这个局部,由于父子朝向都向右,直觉也告诉我们要做一次右-右旋转:B成为k1的右孩子,k1这颗子树成为k2的左孩子。最后把k3的左孩子这颗子树的根变更为k2。
具体细微过程前面单旋转的时候说过了,这里就给出拆掉脚手架后的中间成品
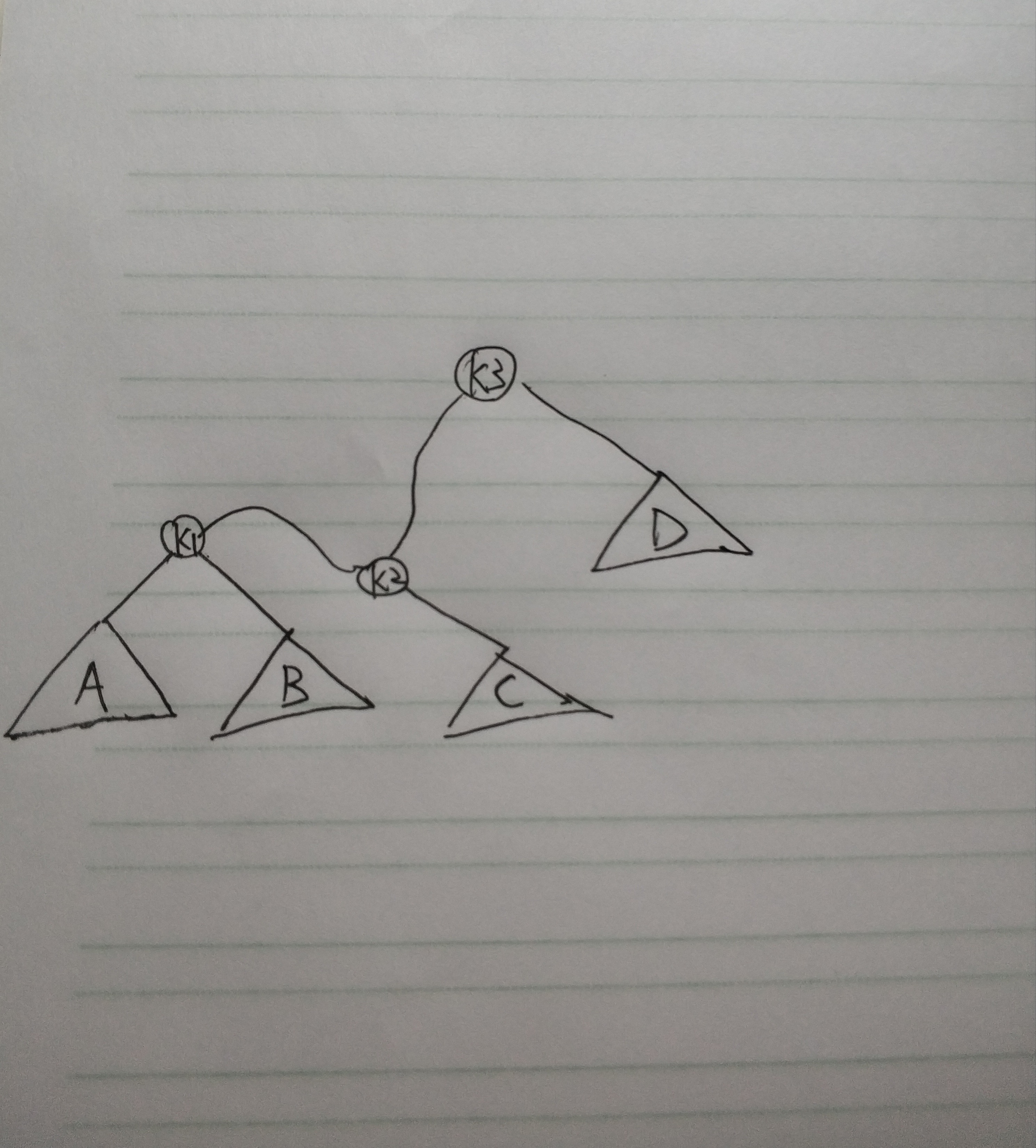
稍微整理一下就更明了了,把k2的高度提上去

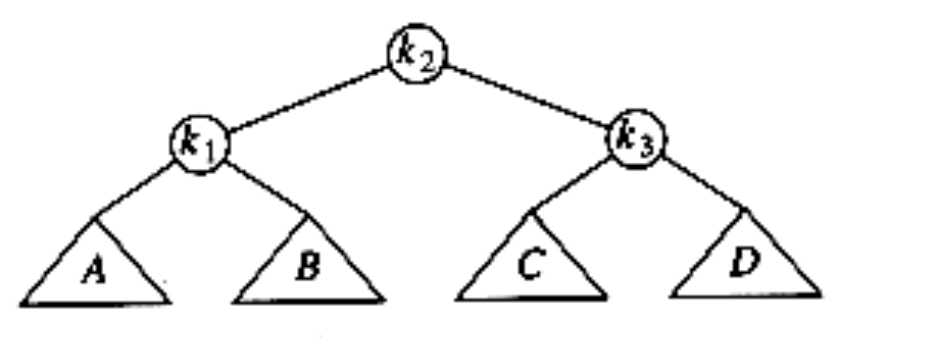
到这一步之后,我们再把k3-k2这个局部,由于此时朝向都为左,那么顺理成章做一次左-左旋转:C成为k3的左孩
子,k3这颗子树成为k2的右孩子。至此,左-右旋转完成,全树的高度得到了控制。

// This function can be called only if K3 has a left // child and K3's left child has a right child // Do the left-right double rotation // Update heights, then return new root static Position DoubleRotateWithLeft( Position K3 ) { // Rotate between K1 and K2 K3->lc = SingleRotateWithRight( K3->lc ); // Rotate between K3 and K2 return SingleRotateWithLeft( K3 ); }
这四种旋转策略已经覆盖了插入操作失衡的所有情况,下面给出总的插入操作,汇总了这四种情况。
AvlTree Insert( int X, AvlTree T ) { if( !T ){//这里是实质的插入部分,无中生有 //创建并返回一个单节点树 T = (Position)malloc( sizeof( struct AvlNode ) ); if( !T ) printf("Fatal Error: Out Of Space! ");//错误检测 else{ T->value = X; T->Height = 0; T->lc = T->rc = nullptr; } } //还未走到应插入的地点时 else if( X < T->value ) //遵循BST的规则,new value < root value,往左走 { T->lc = Insert( X, T->lc );//此时插入完成后,t指向被插入节点的父亲 if( Height( T->lc ) - Height( T->rc ) == 2 ) //如果新插入节点后lc比rc深2层,那么就是情形1,2 if( X < T->lc->value )//如果是这样,根据BST规则,是左-左 T = SingleRotateWithLeft( T ); else //否则是左-右 T = DoubleRotateWithLeft( T ); /* 我们需要根据情况去采取不同的旋转策略,使其恢复平衡 单旋转调整了情形1:发生在外侧,对a的lc->lc插入 双旋转调整了情形2:发生在内侧,对a的lc->rc插入 */ } else if( X > T->value ) { T->rc = Insert( X, T->rc ); //遵循BST的规则,new value > root value,往右走 if( Height( T->rc ) - Height( T->lc ) == 2 ) //如果新插入节点后右子树更高,那么就是情形3,4 if( X > T->rc->value ) //如果是这样,根据BST规则,是右-右 T = SingleRotateWithRight( T ); else //否则是右-左 T = DoubleRotateWithRight( T ); /* 这个分支里 单旋转调整了情形3:发生在外侧,对a的rc->rc插入 双旋转调整了情形4:发生在内侧,对a的rc->lc插入 */ } /* Else X is in the tree already; we'll do nothing */ T->Height = max( Height( T->lc ), Height( T->rc ) ) + 1; return T; }
最后可以做一个很直观的比较:分别构建大数据量的BST和AVLT,比较他们的高度,就可以明显看出平衡操作对于高度的有效控制了,给一个完整版本的实现吧,可以对比下和普通BST的层数差距。
1 #include "avltree.h" //这里只给出.c的部分,头文件就是前文的类型声明+各种函数签名 2 #include <stdlib.h> 3 #include <stdio.h> 4 #include <time.h> 5 6 7 int max(int a,int b){return a>b?a:b;} 8 9 10 11 int updateH(AvlTree x){ 12 return x->Height = 1 + max ( Height ( x->lc ), Height ( x->rc ) ); 13 } 14 15 16 AvlTree 17 MakeEmpty( AvlTree T ) 18 { 19 if( T != NULL ) 20 { 21 MakeEmpty( T->lc ); 22 MakeEmpty( T->rc ); 23 free( T ); 24 } 25 return NULL; 26 } 27 28 29 30 31 void Preorder(Position root); 32 33 int main() { 34 srand(time(NULL)); 35 AvlTree a=nullptr; 36 int nodeCnt,del; 37 printf("Please input how many nodes in the avl tree: "); 38 scanf("%d",&nodeCnt); 39 for(int i=0;i<nodeCnt;i++) a=Insert(rand()%(nodeCnt<<1), a); 40 Preorder(a); 41 printf(" The height of avlt with %d nodes is : %d ",nodeCnt,Height(a)); 42 // scanf("%d",&del); 43 // DeleteInAVL(del, a); 44 // Preorder(a); 45 } 46 47 Position 48 Find( int X, AvlTree T ) 49 { 50 if( !T ) 51 return NULL; 52 if( X < T->value ){ 53 return Find( X, T->lc ); 54 } 55 else 56 if( X > T->value ) 57 return Find( X, T->rc ); 58 else 59 return T; 60 } 61 62 Position 63 FindMin( AvlTree T ) 64 { 65 if( !T ) 66 return NULL; 67 else 68 if( T->lc == NULL ) 69 return T; 70 else 71 return FindMin( T->lc ); 72 } 73 74 Position 75 FindMax( AvlTree T ) 76 { 77 if( T != NULL ) 78 while( T->rc != NULL ) 79 T = T->rc; 80 81 return T; 82 } 83 84 85 // This function can be called only if g has a left child 86 // Perform a rotate between a node (g) and its left child 87 // Update heights, then return new root 88 89 static Position 90 SingleRotateWithLeft( Position p ) //左-左的情况 91 { 92 Position temp; 93 94 temp = p->lc; 95 p->lc = temp->rc; 96 97 temp->rc = p; 98 99 p->Height = max( Height( p->lc ), Height( p->rc ) ) + 1; 100 temp->Height = max( Height( temp->lc ), p->Height ) + 1; 101 102 return temp; /* New root */ 103 } 104 105 106 // This function can be called only if g has a right child 107 // Perform a rotate between a node (g) and its right child 108 // Update heights, then return new root 109 110 static Position 111 SingleRotateWithRight( Position g ) //右-右的情况 112 { 113 Position temp; 114 115 temp = g->rc; 116 g->rc = temp->lc; 117 118 temp->lc = g; 119 120 g->Height = max( Height( g->lc ), Height( g->rc ) ) + 1; 121 temp->Height = max( Height( temp->rc ), g->Height ) + 1; 122 123 return temp; /* New root */ 124 } 125 126 127 // This function can be called only if K3 has a left 128 // child and K3's left child has a right child 129 // Do the left-right double rotation 130 // Update heights, then return new root 131 132 static Position 133 DoubleRotateWithLeft( Position K3 ) //左-右的情况 134 { 135 /* Rotate between K1 and K2 */ 136 K3->lc = SingleRotateWithRight( K3->lc ); 137 138 139 /* Rotate between K3 and K2 */ 140 return SingleRotateWithLeft( K3 ); 141 } 142 143 // This function can be called only if g has a right 144 // child and g's right child has a left child 145 // Do the right-left double rotation 146 // Update heights, then return new root 147 148 static Position 149 DoubleRotateWithRight( Position g ) //右-左的情况 150 { 151 // Rotate between p and v, p means g->rc 152 g->rc= SingleRotateWithLeft( g->rc ); 153 154 155 // Rotate between g and p 156 return SingleRotateWithRight( g ); 157 } 158 159 160 AvlTree 161 Insert( int X, AvlTree T ) 162 { 163 Position p;// it means p on the "new node" 164 if( !T ){//这里是实质的插入部分,无中生有 165 //创建并返回一个单节点树 166 T = (Position)malloc( sizeof( struct AvlNode ) ); 167 if( !T ) printf("Fatal Error: Out Of Space! ");//错误检测 168 else{ 169 T->value = X; 170 T->Height = 0; 171 T->lc = T->rc = nullptr; 172 } 173 } 174 175 //还未走到应插入的地点时 176 else 177 if( X < T->value ) //遵循BST的规则,new value < root value,往左走 178 { 179 T->lc = Insert( X, T->lc ); 180 //此时插入完成后,T指向被插入节点的父亲,新生节点作为T的左孩子而存在。 181 182 if( Height(T->lc)-Height(T->rc) == 2 ) 183 //如果新插入节点后lc比rc深2层,那么就是情形1,2 184 if( X < T->lc->value )//如果是这样,根据BST规则,是左-左 185 T = SingleRotateWithLeft( T ); 186 else //否则是左-右 187 T = DoubleRotateWithLeft( T ); 188 /* 189 我们需要根据情况去采取不同的旋转策略,使其恢复平衡 190 单旋转调整了情形1:发生在外侧,对a的lc->lc插入 191 双旋转调整了情形2:发生在内侧,对a的lc->rc插入 192 */ 193 194 195 } 196 else 197 if( X > T->value ) //遵循BST的规则,new value > root value,往右走 198 { 199 T->rc = Insert( X, T->rc ); 200 //此时插入完成后,T指向被插入节点的父亲,新生节点作为T的右孩子而存在。 201 if( Height(T->rc)-Height(T->lc) == 2 ) 202 //如果新插入节点后右子树更高,那么就是情形3,4 203 if( X > T->rc->value ) //如果是这样,根据BST规则,是右-右 204 T = SingleRotateWithRight( T ); 205 else //否则是右-左 206 T = DoubleRotateWithRight( T ); 207 /* 208 这个分支里 209 单旋转调整了情形3:发生在外侧,对a的rc->rc插入 210 双旋转调整了情形4:发生在内侧,对a的rc->lc插入 211 */ 212 213 // 214 } 215 216 /* Else X is in the tree already; we'll do nothing */ 217 218 updateH(T); 219 return T; 220 } 221 222 223 int 224 Retrieve( Position P ) 225 { 226 return P->value; 227 } 228 229 230 void Preorder(Position root){ 231 if (root) { 232 printf("%d ",root->value); 233 Preorder(root->lc); 234 Preorder(root->rc); 235 } 236 }
祝食用愉快2333
ps.转载请注明文章来源,否则会追加法律责任。
