今天是本蒟蒻在杭州集训(被虐)的第四天,由于我太弱了,出题人不屑于浪费时间出毒瘤题来坑我;而是从洛谷上
挪了些原题上来;但由于我太弱了,还是没做出来;
T1 . 坐等 memset0
树链剖分是个喜欢逛讨论区的女孩子。
树链剖分看到有若干个小学生发的帖子,因为一些原因,这些帖子形
成了一条链。
其中第 i(1<=i< n)个帖子和第 i+1 个帖子用双向边相连
树链剖分举报了这些帖子,然后作为管理员的 memset0,决定对帖子
进行删除。
其中第 i 个帖子有一个小学生值 a.
但是, 因为 memset0 太强了, memset0 不屑于对小学生值在[l,r] 区
间内的帖子进行删除,只和谐掉其他帖子。(即,只保留小学生值[l,r
的帖子)
现在,树链剖分想到一个问题,就是在这个保留下来的帖子里,联通
块的个数是多少。
问题还没完
我们把只保留小学生值[l,r]的帖子使得这些帖子的联通块的个数记
为
求 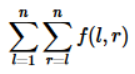
输入:
第一行一个正整数 n
第二行 n 个正整数 a[i]
输出
一行一个正整数,表示答案
样例输入
4
2 1 1 3
样例输出
11
对于 40%的数据 n <= 100
对于 60%数据 n <= 1000
对于 100%数据 n <= 100000,1<=a[i]<=n 且为正整数
这题在洛谷原题是CF1151E有兴趣的可以去做一下;
然后,我讲下这题怎么做,首先如果打暴力的话是只有60分;
接下来,我讲讲从隔壁大佬那学来的正解:
考虑每个点对答案的贡献,我们认为一个连通块里让编号最大的点
产生贡献,对于点 i,要产生贡献就一定要这个点存在,而点 i+1不
存在而点n只用包含这个点就行了
具体是这样的:
当 a i>a i+1 贡献=(a i-a i+1)*(n-a i+1)
当 a i<a i+1 贡献=(a i+1-a i)*a i;
具体代码如下:
#include<bits/stdc++.h> using namespace std; long long n; long long ans; long long a[1000005]; int main() { scanf("%lld",&n); for(int i=1;i<=n;i++) { scanf("%lld",&a[i]); } for(int i=1;i<n;i++) { int x=a[i],y=a[i+1]; if(x>y) { ans=(long long)ans+(x-y)*(n-x+1); } else { ans=ans+(long long)(y-x)*x; } } ans+=(long long)a[n]*(n-a[n]+1); cout<<ans; return 0; }
这题也是洛谷原题,题号是:CF1146D;
这题写暴力的话只有40分;
下面我来说一下正解:
先暴力求出前2*max(a,b)的方案数
在通过打表找到规律:
当 i>2*max(a,b)时;
f(i)=i/gcd(a,b)+1;
(其实i > a+b就有规律了)
关于这个规律的证明
首先用exgcd可以说明 不是gcd(a,b)倍数的点无法到达
ax-by = gcd(a,b)*k
现在可以用exgcd求出x,y
然后我们就是要走x个a,y个b
假如a < b的话
那么就wxw就可以走若干个+a,直到大于b时候往回跳一次,然后继续+a
a>b同理
代码如下:
#include<bits/stdc++.h> using namespace std; long long n; long long ans; long long a,b,i; long long gcd(long long a,long long b){return b?gcd(b,a%b):a;} int main() { scanf("%lld%lld%lld",&n,&a,&b); ans+=a; int d=gcd(a,b); if(n<a){ printf("%d",n+1); return 0; } long long tot=1,w=0; for(i=a;i<=2*max(a,b);i++) { while(w+a<=i) { tot+=(i-w)/a; w+=(i-w)/a*a; tot+=w/b; w-=w/b*b; if(!w) break; }if(!w) break; ans+=tot; if(i==n) break; } if(!w) { long long d=gcd(a,b); long long g=i/d+1; long long k=n/d+1; long long sum=(long long)(n/d)*d; ans+=(long long)(g+k)*(sum-i+d)/2; long long total=0; for(long long j=n+1;j<sum+d;j++) { total+=(long long)j/d+1; } ans-=total; } cout<<ans; return 0; }
样例输入 5 2
4 3 1 5 2
1 1 4 3
2 2 5 3
样例输出
2
4
第一个询问,从p-1到0枚举答案,求逆,判断是否在区间[l,r]内,如果在就输出并退出
第二个询问一样,从n~1枚举答案,倍增(或用成环,因为是个排列)判断k步前是哪个点。
代码如下:
#include<bits/stdc++.h> using namespace std; int n,m; struct adw{ int ma,zhi; }a[110005]; int b,l,r,p,k,z; int f[110000]; int fa[110000][21]; int w[21]; int q[110000]; int rd(){ int s=0,ff=1; char ww=getchar(); while(ww<'0'||ww>'9'){ if(ww=='-') ff=-1; ww=getchar(); } while(ww>='0'&&ww<='9'){ s=s*10+(ww-'0'); ww=getchar(); } return s*ff; } int kuai(int a,int b,int p) { int sum=1; while(b) { if(b&1) sum=(long long)sum*a%p; a=(long long)a*a%p; b=(b>>1); } return sum; } void work() { bool h=0; for(int i=p-1;i>=0;i--) { int c=kuai(i,p-2,p); for(int j=c;j<=n;j+=p) { if(a[j].ma>=l&&a[j].ma<=r) { printf("%d ",i); h=1; break; } } if(h==1) break; } } void dfs(int x,int d) { if(f[x]){q[x]=d; return;} f[x]=1; dfs(a[x].zhi,d+1); q[x]=q[a[x].zhi]; } int QWQ(int x,int s) { for(int i=z;i>=0;i--) { if(s>=w[i]) { s-=w[i]; x=fa[x][i]; } } return x; } void QwQ() { for(int i=n;i>=1;i--) { int ch=QWQ(i,k%q[i]); if(ch>=l&&ch<=r) { printf("%d ",i); break; } } } int main() { n=rd(); m=rd(); w[0]=1; z=log2(n); for(int i=1;i<=n;i++) { a[i].zhi=rd(); a[a[i].zhi].ma=i; fa[i][0]=a[i].zhi; } for(int i=1;i<=z;i++) w[i]=(w[i-1]<<1); for(int i=1;i<=n;i++) if(f[i]==0) dfs(i,0); for(int i=1;i<=z;i++) for(int j=1;j<=n;j++) fa[j][i]=fa[fa[j][i-1]][i-1]; for(int i=1;i<=m;i++) { b=rd(); if(b==1) { l=rd(); r=rd(); p=rd(); work(); } if(b==2) { l=rd(); r=rd(); k=rd(); QwQ(); } } return 0; }
对了,记得一定要用read函数读入,不然会被卡,不要问我我为什么会知道;
以上就是我被虐的全部过程;
来自一个蒟蒻;