Amr doesn't like Maths as he finds it really boring, so he usually sleeps in Maths lectures. But one day the teacher suspected that Amr is sleeping and asked him a question to make sure he wasn't.
First he gave Amr two positive integers n and k. Then he asked Amr, how many integer numbers x > 0 exist such that:
- Decimal representation of x (without leading zeroes) consists of exactly n digits;
- There exists some integer y > 0 such that:
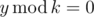 ;
;- decimal representation of y is a suffix of decimal representation of x.
As the answer to this question may be pretty huge the teacher asked Amr to output only its remainder modulo a number m.
Can you help Amr escape this embarrassing situation?
Input consists of three integers n, k, m (1 ≤ n ≤ 1000, 1 ≤ k ≤ 100, 1 ≤ m ≤ 109).
Print the required number modulo m.
1 2 1000
4
2 2 1000
45
5 3 1103
590
A suffix of a string S is a non-empty string that can be obtained by removing some number (possibly, zero) of first characters from S.
题意是统计n位数x , 它有一个后缀y,能够满足( y%k==0)的 x 的个数.我做法是开一个3维数组 , dp[i][j][y] 。 表示符合前 i 位 , 余数是j, 是否有前导 0 的数的个数。
首先要预处理了 i*j^10 % k 的结果,( i = 1~9 , j = 1~n )用于对新的状态的转移。
预处理好排列数 10^j % m ,当出现后缀y符合条件且没前导0 ,可进行计算。
剩下就是状态转移了 。
转移的过程中 无前导0 且 余数等于0 的可以进行一次计数。
否则就继续进行转移就OK 。
代码写得比较恶心...然后要注意处理好边界就没什么问题了。

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N = 1010 ; const int M = 110 ; LL dp[N][M][2] , n , m , k , cnt[N] , rest[10][N]; void init() { cnt[0] = 1 ; for( int i = 1 ; i <= n ; ++i ) { cnt[i] = cnt[i-1] * 10 % m ; } for( int j = 1 ; j <= n ; ++j ) { for( int i = 1 ; i < 10 ; ++i ) { if( j == 1 ) rest[i][j] = i % k ; else rest[i][j] = ( 10 % k * rest[i][j-1] ) % k ; // cout << i << ' ' << j << ' ' << rest[i][j] << endl ; } } memset( dp , 0 , sizeof dp ); for( int i = 0 ; i < 10 ; ++i ) dp[1][i%k][!i]++; // cout << "Run" << endl ; } void Run() { LL ans = 0 ; if( n == 1 ) { for( int i = 1 ; i < 10 ; ++i ) if( i % k == 0 ) ans ++ , ans %= m; } else { for( int i = 1 ; i <= n ; ++i ) { for( int j = 0 ; j < k ; ++j ) { for( int y = 0 ; y < 2 ; ++y ) { if( !y && !j ) { // no leading zero and reminder equal zero if( i < n ) ans = ( ans + 9 * cnt[n-i-1] % m * dp[i][j][y] ) % m ; else ans += dp[i][j][y] , ans %= m ; } else { // leading zero or reminder not equal zero for( int z = 0 ; z < 10 ; ++z ) { int i1 = i + 1 , j1 = ( rest[z][i1] + j ) % k ; dp[i1][j1][!z] += dp[i][j][y] , dp[i1][j1][!z] %= m ; } } } } } } cout << ans << endl ; } int main() { // freopen("in.txt","r",stdin); while( cin >> n >> k >> m ) init() , Run(); }
