1.认识时间复杂度
常数时间的操作:一个操作如果和数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。
时间复杂度为一个算法流程中,常数操作数量的指标。常用O(读作big O)来表示。具体来说,在常数操作数量的表达式中,只要高阶项,不要低阶项,也不要高阶项的系数,
剩下的部分如果记为f(N),那么时间复杂度为O(f(N))。评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是常数项时间。
衡量算法复杂度
1.内存(Memory) 2.时间(Time) 3.指令的数量(Number of Steps) 4.特定操作的数量 磁盘访问数量 网络包数量 5.渐进复杂度(Asymptotic Complexity)
算法的运行时间与什么相关
1.输入的数据。(例如:如果数据已经是排好序的,时间消耗可能会减少。) 2.输入数据的规模。(例如:6 和 6 * 109) 3.运行时间的上限。(因为运行时间的上限是对使用者的承诺。)
算法分析要保持大局观(Big Idea),其基本思路:
1.忽略掉那些依赖于机器的常量。
2.关注运行时间的增长趋势。
比如:T(n) = n3 + 99n3 + 9999 的趋势就相当于 T(n) = Θ(n3)。
渐近记号(Asymptotic Notation)通常有 O、 Θ 和 Ω 记号法。big O 表示按算法最差表现估算,big θ 表示按算法平均表现估算,big Ω 表示按算法最好表现估算。尽管技术上 Θ 记号较为准确,但通常仍然使用 O 记号表示。
使用 O 记号法(Big O Notation)表示最坏运行情况的上界。例如,
1.线性复杂度 O(n) 表示每个元素都要被处理一次。
2.平方复杂度 O(n2) 表示每个元素都要被处理 n 次。
| Notation | Intuition | Informal Definition |
 |
f is bounded above by g asymptotically |
|
 |
Two definitions : f is not dominated by g asymptotically Complexity theory: f is bounded below by g asymptotically |
|
 |
f is bounded both above and below by g asymptotically |
|
2.简单排序
2.1 选择排序
选择排序(Select Sort) 是直观的排序,通过确定一个 Key 最大或最小值,再从带排序的的数中找出最大或最小的交换到对应位置。再选择次之。双重循环时间复杂度为 O(n^2)
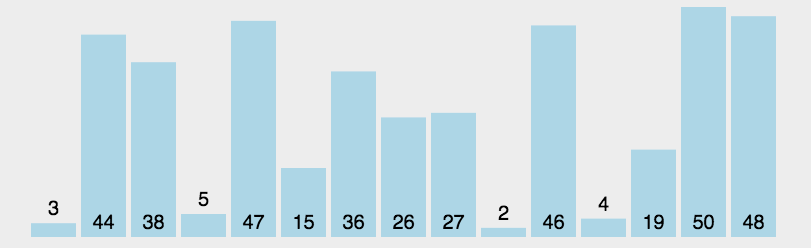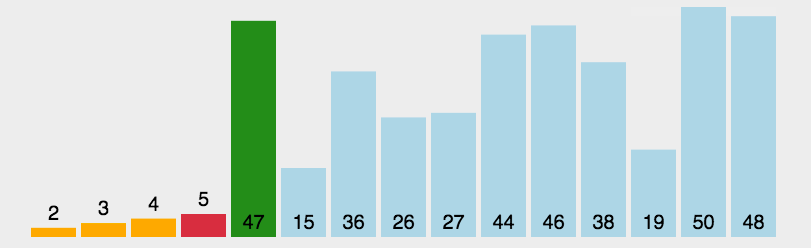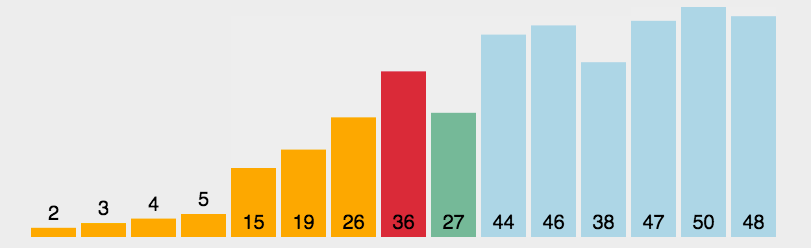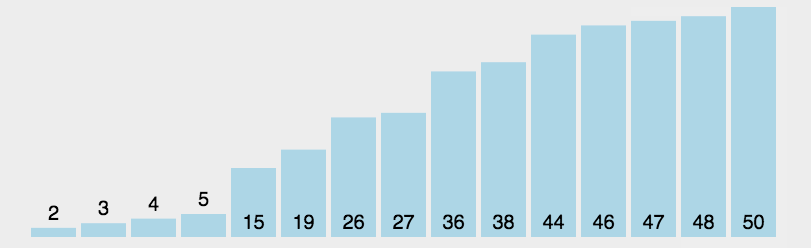
private void sellectionSorted(int[] arr){ if(arr == null || arr.length <=1){ return; } // i ~ N-1 for(int i=0;i<arr.length-1;i++){ int minIndex=i; // i ~ N-1 get min for(int j=i+1;j<arr.length;j++){ minIndex = arr[j] < arr[minIndex] ? j : minIndex; } swap(arr ,minIndex,i); } } private void swap(int[] arr, int a, int b){ int tmp = arr[a]; arr[a] = arr[b]; arr[b] = tmp; }
2.2 冒泡排序
冒泡排序(Bubble Sort) 最为简单的一种排序,通过重复走完数组的所有元素,通过打擂台的方式两个两个比较,直到没有数可以交换的时候结束这个数,再到下个数,直到整个数组排好顺序。因一个个浮出所以叫冒泡排序。双重循环时间 O(n^2)
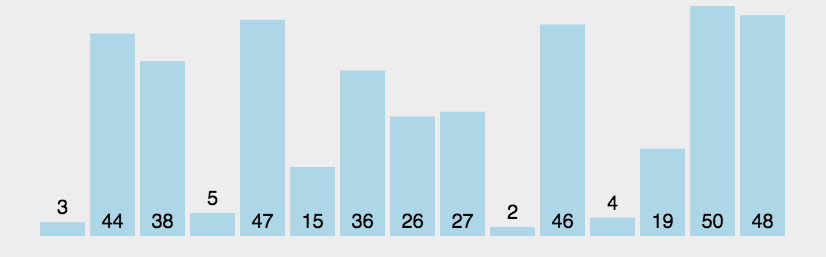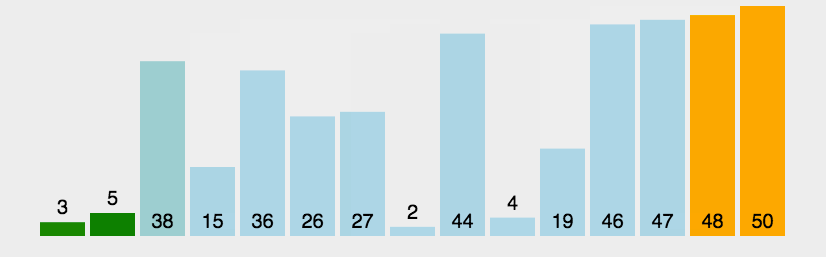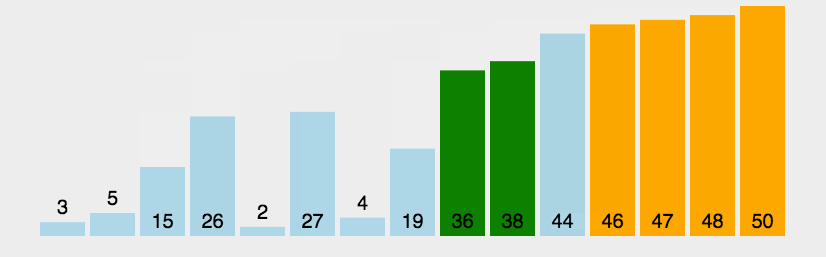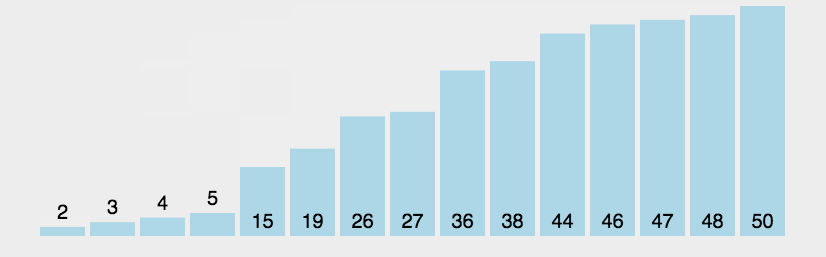
private void bubbleSorted(int[] arr){ if(arr == null || arr.length <=1){ return; } // i ~ N-1 for(int i=arr.length-1;i>0;i--){ // i ~ N-1 set max to the end of arr for(int j=0;j<i;j++){ if(arr[j+1] < arr[j]) { swap(arr ,j+1,j); } } } } // 异或运算 private void swap(int[] arr, int a, int b){ arr[a] = arr[a]^arr[b]; arr[b] = arr[a]^arr[b]; arr[a] = arr[a]^arr[b]; }
2.3 插入排序
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
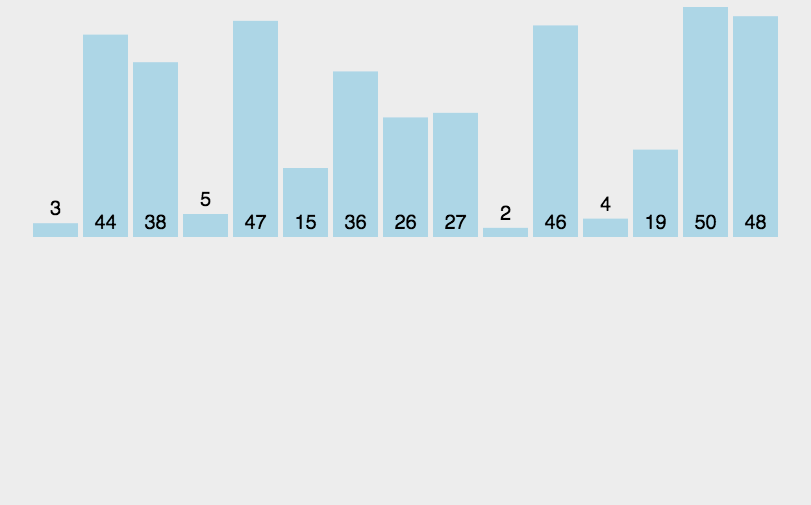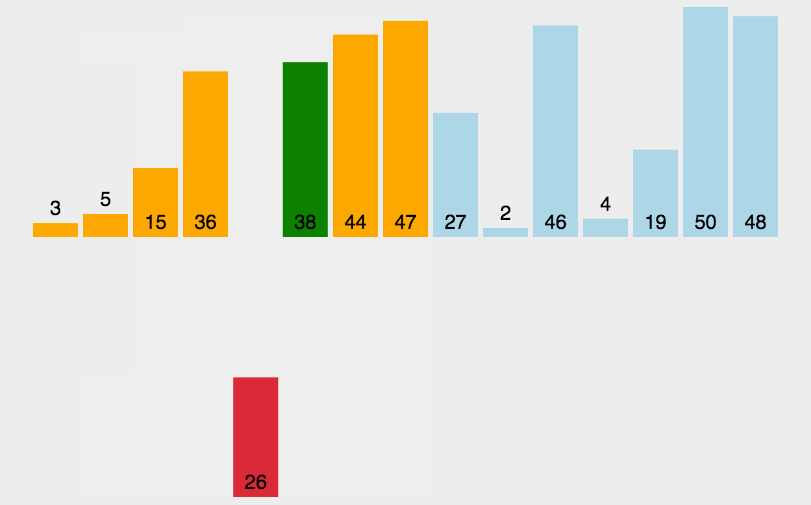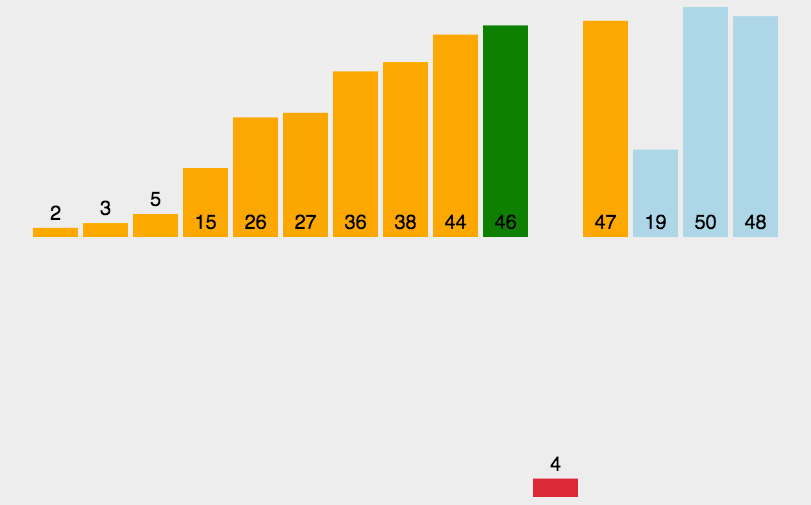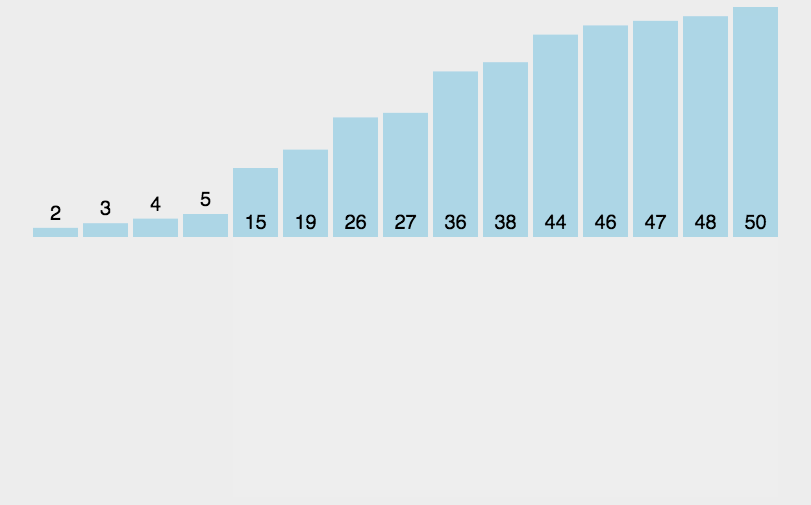
private void insertSorted(int[] arr){ if(arr == null || arr.length <=1){ return; } // 0 ~1 compare and swap // 0 ~2 compare and swap for(int i=0;i<arr.length;i++){ // i ~ N-1 compare and swap for(int j=i;j>0;j--){ if(arr[j-1] > arr[j]) { swap(arr ,j-1,j); } } } } // 异或运算 private void swap(int[] arr, int a, int b){ arr[a] = arr[a]^arr[b]; arr[b] = arr[a]^arr[b]; arr[a] = arr[a]^arr[b]; }
2.4 二分法
二分法查找,也称为折半法,是一种在有序数组中查找特定元素的搜索算法。首先,从数组的中间元素开始搜索,如果该元素正好是目标元素,则搜索过程结束,否则执行下一步。如果目标元素大于/小于中间元素,则在数组大于/小于中间元素的那一半区域查找,然后重复上面的的操作。如果某一步数组为空,则表示找不到目标元素。二分法查找的时间复杂度O(logn)。
private int searchMatch(int[] arr, int low, int high, int target){ if(low > high){ return -1; } int mid = low + ((high-low)>>1); // if(arr[mid] == target){ return mid; } else if(arr[mid] < target){ // search in [mid+1, high] return searchMatch(arr, mid+1, high, target); } else { // search in [low, mid-1] return searchMatch(arr, low, mid-1, target); } }
一般下面几个场景适合二分查找
1.在一个有序数组中,查找某个数是否存在 2.在一个有序数组中,查找>=某个数最左侧位置 3. 在一个无序数组中,任何相邻两数不相等,寻找局部最小值
3.补充
3.1 异或运算
1. 0^N=N, N^N=0
2.异或运算满足交换率和结合率
A^B = B^A, A^(B^C) = (A^B)^C
3.同样一批数,异或运算,先后顺序变化 不影响结果
A^B^...^Z = Z^Y^...^A
4.无进位加法,相同为0,不同为1;
int a= 3= 011
int b= 5= 101
int c= a^b = 011^101=110=6
3.2 取出一个数对应二进制最右侧的1对应的整数
// 与上自己的取反加1
int a= A & (~A+1);
3.3 对数器
1.有一个你想要测的方法A 2.实现一个绝对正确但是复杂度不好的方法B 3.实现一个随机样本产生器 4.实现比对的方法 5.把方法A和方法B比对很多次来验证方法B是否正确。 6.如果有一个样本使得比对出错,打印样本分析是哪个方法出错 7.当样本数量很多时比对测试(假设10万次测试)依然正确,可以确定方法A已经正确


