题目描述
给出一个(n)行(m)列的矩阵,矩阵中每个格子有一个非负整数,现在要求你去除其中的个格子,使得剩下的格子中的数的总和最大。另外,去除(k)个格子后,剩下的格子必须满足以下几个性质:
1.连续性:同一行的格子是连续的,也就是说,剩下的格子不会出现同一行有两个分离的连续段的情况。
2.支撑性:除了底行以外,在其他剩下的行中保留的连续格子段,至少有一个格子与它下一行某个保留的格子处于同一列中。
3.保底性:最后一行至少保留一个格子。
输入输出格式
输入格式
第一行有三个整数(n,m,k(1leq n,mleq 64,max(nm-64,0)leq k<nm)),表示矩阵的大小以及去除格子的个数。
接下来有(n)行,每(m)行个非负整数,表示矩阵的元素。矩阵中每个元素的值不超过(32767)
输出格式
一个整数,表示去除(k)个格子后,剩下的格子中的数的总和的最大值。
样例
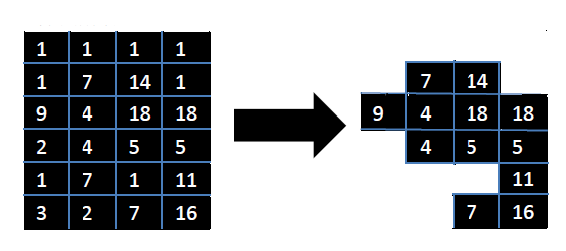
INPUT
6 4 12
1 1 1 1
1 7 14 1
9 4 18 18
2 4 5 5
1 7 1 11
3 2 7 16
OUTPUT
118
HINT
对于(30 ext %)的数据,(n,mleq 5)
对于(60 ext %)的数据,(n,mleq 10)
对于(100 ext %)的数据,(n,mleq 64)
SOLUTION
dp
首先观察题目所给的三个性质:连续性,支撑性,保底性。这三个性质相当于在提示我们dp方程的转移方式。
- 连续性:我们的转移应该是从某层的某个区间段转移到其相邻层的某个区间段。
- 支撑性:转移应该发生在点((i,j))所在的某个区间与点((i-1,j))所在的某个区间之中。
- 保底性:为了使最后一行一定有方格,可以考虑从上往下转移,如此上层可以出现整层不选的情况,而下层则不会。
由上面对性质的分析我们也可以看出转移过程有几个关键字:①区间;②点;而本题又要求删去(k)个方格于是又有③方格数;
不难得出一个简单一点的想法,(dp)数组记四维:(dp[i][l][r][k])表示取第(i)行的区间([l,r])选择了(k)个的情况。但是,如此设置(dp)数组会使时间复杂度达到(O(n^6))的级别(枚举(i),枚举本层(l,r),枚举(k),枚举上层的(l‘,r’)),虽然本题的数据范围非常小,(nleq 64),按照这个时间复杂度,枚举量仍然能够达到(2^{36})(虽然有很多种情况是废弃的)所以这种(dp)方式只能用来暴力拿部分分。
转移关键字应该是没有错的,那么如何优化呢?
-
考虑区间的性质,区间可以通过一个端点+区间长度+从该点出发表示该区间的延伸方向表示,由于方向只可能有两种(向左或向右)那么我们一样可以通过枚举端点和区间长度来得到一个区间。
-
而区间长度其实只是用来计算方格内数值的,所以还有(k)个方格可选时,“区间长度为(len)”这个信息其实是用来辅助计算(k-len)个可选时的最优方案的。换而言之,就是计算到最后我们并不关心这个答案是从多长的区间转移来的,所以可以优化掉这一维,区间长度(len)值作为一个中间值不被记录在(dp)数组里。
-
没有区间长度,怎么判断支撑性呢?别忘了支撑性可以通过点与点来判断,我们把区间转化为一个个关键点来考虑。所谓关键点就是某个区间的某个端点,接下来我们讨论的就是这个问题。
我们记两个数组(lft[i][j][k],rgt[i][j][k]),表示右/左端点为点((i,j))的某区间,而转移到此时,剩余可选的方格数为(k)。
因为为了优化复杂度,我们把三维的区间改成了二维的关键点,那么相应地,转移方面就要稍微复杂一些。
-
同层转移:对于(lft[i][j][k])显然可以看作由(lft[i][j-1][k-1])加上点((i,j))的值构成的答案。
-
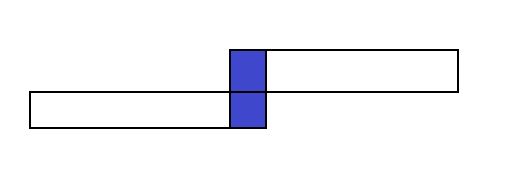
上下层关键点转移:很两个关键点上下相邻的区间一定是合法的,我们就可以通过枚举本层区间长度(len),通过已经枚举而已知的(k)算出上层的状态进行转移。这是“关键-->关键”。
-
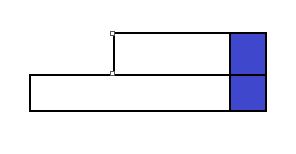
上层非关键点转移:而对于那种本层的关键点的上层对应点不是关键点的情况,其实也可以转化成关键点之间的转移来做,只要在已知左端点(p)的区间的左边再加上一段区间就可以构成(p)不是关键点的区间,(而区间长度恰巧也要枚举(len),可以把转移2和转移3一起在(len)的循环中完成)这么做就可以做到“非关键-->关键”。

而由于我们会做同层转移所以转移3在本层只取一个点也不会遗漏情况。
如此一来时间复杂度自然就降到(O(n^4))了。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
using namespace std;
typedef long long LL;
#define Max(a,b) ((a>b)?a:b)
#define Min(a,b) ((a<b)?a:b)
const int N=70;
const int INF=1000010000;
int n,m,K,lft[N][N][N],rgt[N][N][N],sum[N][N];
short sq[N][N];
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9') {x=x*10+ch-48;ch=getchar();}
return x*f;}
int main(){
int i,j;
n=read();m=read();K=read();K=n*m-K;
memset(lft,0,sizeof(lft));memset(rgt,0,sizeof(rgt));memset(sum,0,sizeof(sum));
for (i=1;i<=n;++i)
for (j=1;j<=m;++j) sq[i][j]=read();
for (i=1;i<=n;++i)
for (j=1;j<=m;++j) sum[i][j]=sum[i][j-1]+sq[i][j];
for (int k=1;k<=K;++k){
for (i=1;i<=n;++i){
for (j=1;j<=m;++j){
int &L=lft[i][j][k];int &R=rgt[i][j][k];
if (k==1) {L=R=sq[i][j];continue;}
L=R=-INF;
if (j>1) L=lft[i][j-1][k-1]+sq[i][j];
if (j<m) R=rgt[i][j+1][k-1]+sq[i][j];
if (i==1) continue;
for (int len=1;len<=k;++len){
int remn=k-len;
if (len<=j) {L=Max(L,Max(rgt[i-1][j][remn],lft[i-1][j][remn])+sum[i][j]-sum[i][j-len]);}
if ((len+j-1)<=m) {R=Max(R,Max(rgt[i-1][j][remn],lft[i-1][j][remn])+sum[i][j+len-1]-sum[i][j-1]);}
if ((len<=j)&&remn){
int now=rgt[i-1][j][remn]+sum[i-1][j-1]-sum[i-1][j-len]+sq[i][j];
L=Max(L,now);R=Max(R,now);}
if (((len+j-1)<=m)&&remn){
int now=lft[i-1][j][remn]+sum[i-1][j+len-1]-sum[i-1][j]+sq[i][j];
L=Max(L,now);R=Max(R,now);}
}
}
}
}
int ans=0;for (i=1;i<=m;++i) {ans=Max(ans,Max(lft[n][i][K],rgt[n][i][K]));printf("");}
printf("%d
",ans);
return 0;
}