原文参考:http://www.cnblogs.com/Anker/archive/2013/01/22/2871042.html
1、插入排序
输入:n个数(a1,a2,a3,...,an)
输出:输入序列的一个排列(a1',a2',a3',...an')使得(a1'≤a2'≤a3'≤...≤an')。
插入排序的基本思想是:将第i个元素插入到前面i-1个已经有序的元素中。具体实现是从第2个元素开始(因为1个元素是有序的),将第2个元素插入到前面的1个元素中,构成两个有序的序列,然后从第3个元素开始,循环操作,直到把第n元素插入到前面n-1个元素中,最终使得n个元素是有序的。该算法设计的方法是增量方法。书中给出了插入排序的为代码,并采用循环不变式证明算法的正确性。我采用C语言实插入排序,完整程序如下:
1 void insert_sort(int *datas,int length) 2 { 3 int i,j; 4 int key,tmp; 5 //判断参数是否合法 6 if(NULL == datas || 0==length) 7 { 8 printf("Check datas or length. "); 9 exit(1); 10 } 11 //数组下标是从0开始的,从第二个元素(对应下标1)开始向前插入 12 for(j=1;j<length;j++) 13 { 14 key = datas[j]; //记录当前要插入的元素 15 i = j-1; //前面已经有序的元素 16 //寻找待插入元素的位置,从小到到排序,如果是从大到小改为datas[i]<key 17 while(i>=0 && datas[i] > key) 18 { 19 20 datas[i+1] = datas[i]; 21 i--; //向前移动 22 } 23 datas[i+1] = key; //最终确定待插入元素的位置 24 } 25 }
2、归并排序
归并排序采用了算法设计中的分治法,分治法的思想是将原问题分解成n个规模较小而结构与原问题相似的小问题,递归的解决这些子问题,然后再去合并其结果,得到原问题的解。分治模式在每一层递归上有三个步骤:
分解(divide):将原问题分解成一系列子问题。
解决(conquer):递归地解答各子问题,若子问题足够小,则直接求解。
合并(combine):将子问题的结果合并成原问题的解。
归并排序(merge sort)算法按照分治模式,操作如下:
分解:将n个元素分解成各含n/2个元素的子序列
解决:用合并排序法对两个序列递归地排序
合并:合并两个已排序的子序列以得到排序结果
在对子序列排序时,长度为1时递归结束,单个元素被视为已排序好的。归并排序的关键步骤在于合并步骤中的合并两个已经有序的子序列,引入了一个辅助过程,merge(A,p,q,r),将已经有序的子数组A[p...q]和A[q+1...r]合并成为有序的A[p...r]。书中给出了采用哨兵实现merge的伪代码,课后习题要求不使用哨兵实现merge过程。在这个两种方法中都需要引入额外的辅助空间,用来存放即将合并的有序子数组,总的空间大小为n。现在用C语言完整实现这两种方法,程序如下:
1 #include<stdio.h> 2 #include<malloc.h> 3 #define MAXLIMIT 65535 4 5 void MERGE(int *data,int p, int q, int r){ 6 int i,j,k; 7 int n1 = q-p+1; 8 int n2 = r-q; 9 int *left = (int *)malloc((n1+1)*sizeof(int)); 10 int *right = (int *)malloc((n2+1)*sizeof(int)); 11 12 for(i=0;i<n1;i++) { 13 *(left+i) = *(data+p+i); 14 } 15 for(j=0;j<n2;j++){ 16 *(right+j) = *(data+q+j+1); 17 } 18 19 *(left+n1) = MAXLIMIT; 20 *(right+n2) = MAXLIMIT; 21 i=0; 22 j=0; 23 for(k=p;k<=r;k++) { 24 if(*(left+i) <= *(right+j)) { 25 data[k] = *(left+i); 26 i = i+1; 27 } 28 else{ 29 data[k] = *(right+j); 30 j = j+1; 31 } 32 } 33} 34 35 36 void MERGE_SORT(int data[], int p, int r) { 37 int q; 38 if(p < r) { 39 q = (p+r)/2; 40 MERGE_SORT(data, p, q); 41 MERGE_SORT(data, q+1, r); 42 MERGE(data,p,q,r); 43 } 44 } 45 void main() { 46 int A[8]={1, 3, 8, 5, 2, 13, 4, 9}; 47 int i; 48 //printf("%x",A); 49 MERGE_SORT(A,0,7); 50 for(i=0; i<8; i++) { 51 printf("%d",A[i]); 52 } 53 }
另外参考一篇博客http://www.cnblogs.com/bluestorm/archive/2012/09/06/2673138.html
程序也不错:
1 /** 2 * Merge_Sort: 归并排序的递归实现 3 * 注:算法导论上给出的合并排序算法 4 * 递归过程是将待排序集合一分为二, 5 * 直至排序集合就剩下一个元素为止,然后不断的合并两个排好序的数组 6 * T(n) = O(nlgn) 7 **/ 8 #include <stdio.h> 9 #define LEN 8 10 11 // 合并 12 void merge(int a[], int start, int mid, int end) 13 { 14 int n1 = mid - start + 1; 15 int n2 = end - mid; 16 int left[n1], right[n2]; 17 int i, j, k; 18 19 for (i = 0; i < n1; i++) /* left holds a[start..mid] */ 20 left[i] = a[start+i]; 21 for (j = 0; j < n2; j++) /* right holds a[mid+1..end] */ 22 right[j] = a[mid+1+j]; 23 24 i = j = 0; 25 k = start; 26 while (i < n1 && j < n2) 27 if (left[i] < right[j]) 28 a[k++] = left[i++]; 29 else 30 a[k++] = right[j++]; 31 32 while (i < n1) /* left[] is not exhausted */ 33 a[k++] = left[i++]; 34 while (j < n2) /* right[] is not exhausted */ 35 a[k++] = right[j++]; 36 } 37 38 // merge_sort():先排序,再合并 39 void merge_sort(int a[], int start, int end) 40 { 41 int mid; 42 if (start < end) 43 { 44 mid = (start + end) / 2; 45 printf("sort (%d-%d, %d-%d) %d %d %d %d %d %d %d %d ", 46 start, mid, mid+1, end, 47 a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7]); 48 49 // 分解 + 解决:Divide + Conquer 50 merge_sort(a, start, mid); // 递归划分原数组左半边array[start...mid] 51 merge_sort(a, mid+1, end); // 递归划分array[mid+1...end] 52 // 合并:Combine 53 merge(a, start, mid, end); // 合并 54 55 printf("merge (%d-%d, %d-%d) to %d %d %d %d %d %d %d %d ", 56 start, mid, mid+1, end, 57 a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7]); 58 } 59 } 60 61 int main(void) 62 { 63 int a[LEN] = { 5, 2, 4, 7, 1, 3, 2, 6 }; 64 merge_sort(a, 0, LEN-1); 65 66 return 0; 67 }
3、课后习题
有地道题目比较有意思,认真做了做,题目如下:
方法1:要求运行时间为θ(nlgn),对于集合S中任意一个整数a,设b=x-a,采用二分查找算法在S集合中查找b是否存在,如果b存在说明集合S中存在两个整数其和等于x。而二分查找算起的前提是集合S是有序的,算法时间为θ(lgn),因此先需要采用一种时间最多为θ(nlgn)的算法对集合S进行排序。可以采用归并排序算法,这样总的运行时间为θ(nlgn),满足题目给定的条件。
具体实现步骤:
1、采用归并排序算法对集合S进行排序
2、对集合S中任意整数a,b=x-a,采用二分查找算法b是否在集合S中,若在则集合S中存在两个整数其和等于x,如果遍历了S中所有的元素,没能找到b,即集合S中不存在两个整数其和等于x。ps:自己犯得错,二分查找时,让递归处在while循环中,导致一直无法退出循环
代码:

1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h> 4 5 //非递归二叉查找 6 int binary_search(int *datas,int length,int obj) 7 { 8 int low,mid,high; 9 low = 0; 10 high = length; 11 while(low < high)//变换low 和 high的值,愈来愈逼近循环退出条件 12 { 13 mid = (low + high)/2; 14 if(datas[mid] == obj) 15 return mid; 16 else if(datas[mid] > obj) 17 high = mid; 18 else 19 low = mid+1; 20 } 21 return -1; 22 } 23 #if(0) //自己的错误方法,递归处在while循环之下多半就是有问题的 24 //递归形式二分查找 25 int binary_search_recursive(int *datas,int beg,int end,int obj) 26 { 27 int pos = (beg+end)/2; 28 while(beg < end) { 29 if(obj<datas[pos]){ 30 binary_search_recursive(datas,beg,pos,obj); 31 } 32 else if(obj>datas[pos]) { 33 binary_search_recursive(datas,pos,end,obj); 34 } 35 else 36 return -1; 37 } 38 return 0; 39 } 40 #endif 41 #if(1) 42 //递归形式二分查找 43 int binary_search_recursive(int *datas,int beg,int end,int obj) 44 { 45 int mid; 46 if(beg < end) 47 { 48 mid = (beg+end)/2; 49 if(datas[mid] == obj) 50 return mid; 51 if(datas[mid] > obj) 52 return binary_search_recursive(datas,beg,mid,obj); 53 else 54 return binary_search_recursive(datas,mid+1,end,obj); 55 56 } 57 return -1; 58 } 59 #endif 60 //合并子程序 61 void merge(int *datas,int p,int q,int r) 62 { 63 //int n1 = p-q+1;//粗心导致的错误!!!! 64 int n1= q-p+1; 65 int n2 = r-q; 66 int k,i,j; 67 68 int left[n1],right[n2];//malloc方法也行的 69 for (i = 0; i < n1; i++) /* left holds a[start..mid] */ 70 left[i] = datas[p+i]; 71 for (j = 0; j < n2; j++) /* right holds a[mid+1..end] */ 72 right[j] = datas[q+1+j]; 73 //memcpy(left,datas+p,n1*sizeof(int));//都可以使用 74 // memcpy(right,datas+q+1,n2*sizeof(int)); 75 76 i=0;j=0; 77 for(k=p; k<=r; k++ ) { 78 79 if(i == n1 || j == n2) { 80 break; 81 } 82 if(left[i]<=right[j]){ 83 datas[k] = left[i]; 84 i++; 85 } 86 else { 87 datas[k] = right[j]; 88 j++; 89 } 90 } 91 while(i!=n1) { 92 datas[k++] = left[i++]; 93 } 94 while(j!=n2) { 95 datas[k++] = right[j++]; 96 } 97 98 } 99 //归并排序 100 void merge_sort(int *datas,int beg,int end) 101 { 102 int pos; 103 if(beg < end) { 104 pos = (beg + end)/2; 105 merge_sort(datas,beg,pos); 106 merge_sort(datas,pos+1,end); 107 merge(datas,beg,pos,end); 108 } 109 } 110 111 int main(int argc,char *argv[]) 112 { 113 int i,j,x,obj; 114 int datas[10] = {34,11,23,24,90,43,78,65,90,86}; 115 if(argc != 2) 116 { 117 printf("input error. "); 118 exit(0); 119 } 120 x = atoi(argv[1]); 121 merge_sort(datas,0,9); 122 for(i=0;i<10;i++) 123 { 124 obj = x - datas[i]; 125 j = binary_search_recursive(datas,0,10,obj); 126 //j = binary_search(datas,10,obj); 127 if( j != -1 && j!= i) //判断是否查找成功 128 { 129 printf("there exit two datas (%d and %d) which their sum is %d. ",datas[i],datas[j],x); 130 break; 131 } 132 } 133 if(i==10) 134 printf("there not exit two datas whose sum is %d. ",x); 135 exit(0); 136 }
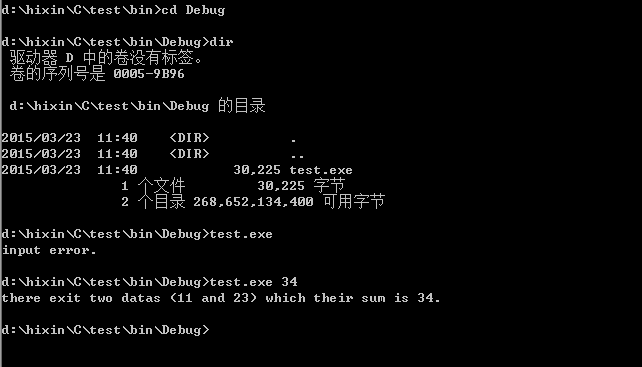
方法2:网上课后习题答案上面给的一种方法,具体思想如下:
1、对集合S进行排序,可以采用归并排序算法
2、对S中每一个元素a,将b=x-a构造一个新的集合S',并对S’进行排序
3、去除S和S'中重复的数据
4、将S和S'按照大小进行归并,组成新的集合T,若干T中有两队及以上两个连续相等数据,说明集合S中存在两个整数其和等于x。
例如:S={7,10,5,4,2,5},设x=11,执行过程如下:
对S进行排序,S={2,4,5,5,7,10}。
S'={9,7,6,6,4,1},排序后S’={1,4,6,6,7,9}。
去除S和S'中重复的数据后S={2,4,5,7,10},S'={1,4,6,7,9}
归纳S和S'组成新集合T={1,2,4,4,5,6,7,7,9,10},可以看出集合T中存在两对连续相等数据4和7,二者存在集合S中,满足4+7=11。
