论文编号:p415-shen
问题:
现有的寻找社会群体的研究主要集中在社交网络中的密集子图。然而,寻找社会脆弱的群体也有许多重要的应用。在本文中,我们引入了K三角的概念来度量群的最小值。然后,我们制定了一个新的研究问题,最小K三角形断开组(MKTG),以找到一个社会脆弱的群体从在线社交网络。我们证明了MKTG是任意图中任意比率内的NPHard和不可逼近的,但在阈值图中是多项式时间可跟踪的。设计了两种算法,即TARA和TRA-ADV,利用图论方法有效地解决了一般图上的MKTG问题。在七个真实数据集上的实验结果表明,所提出的算法在效率和解决方案质量方面优于现有方法。
1. 引言:
与在线社交网络(OSNs)的普及和广泛的可访问性,例如,脸谱网,LIVE-JOLL,LinkedIn,寻找各种社会群体的社区检测研究(14)和活动协调(15, 17)引起了越来越多的关注。现有的研究工作主要集中于从在线社交网络中提取社交连接的个人密集群组。然而,社会脆弱组(STG),即子图,很少有社会交往和成员之间的弱关系,没有得到太多的研究关注。我们认为,STGs有许多实际需要,例如心理教育团体的形成和审稿人的选择,因此值得更多的研究工作。
1.只减少组中的边数不足以满足实际应用(稍后解释)。
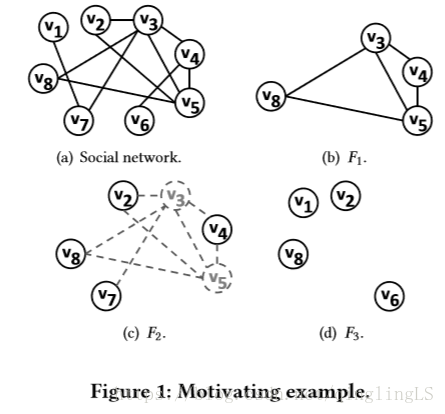
图1:激励示例。
心理教育团体的形成。
对于药物滥用治疗的团体治疗,一个重要的任务是形成心理教育或认知行为团体〔9〕。除了选择具有相似的障碍症状和行为的个体外,群体形成的一个基本标准是分配不认识彼此的患者(有时甚至不是多跳朋友)来形成STG〔9〕。形成这样一个STG是至关重要的参与小组成员,他们的感觉不满足。此外,这样的STG的成员不太可能形成亚组,其可以在治疗期间对抗其他成员。考虑一个临床心理学家希望从图1(A)中选出四名患者(他们的社会关系被说明)来形成心理教育治疗组的情景。注意,F1={3,V4,V5,V8}(见图1(b))可能不是一个好的选择,因为它们之间有许多边缘(社会关系)。虽然f2= {v2,v4,v7,v8}(见图1(c))不具有直接的社会关系,但它们每一对形成朋友关系的朋友(通v3或v5),这可能导致子群(由于普通朋友)或使他们犹豫分享他们的私人经验(可能泄露给共同的)。朋友们)如图所示,F3={V1、V2、V6、V8}(见图1(D))是最好的选择,因为患者不诱导朋友关系的直接或朋友,将治疗组共享的私人信息的机会最小化。
审稿人的选择。
STG也在论文综述中得到应用。会议程序需要指定专家库论文。除了将审稿人的专业知识与专题报告相匹配之外,还应避免让审稿人在社会上相互接近,以及论文作者,以确保无偏见的评估。同时,为了避免利益冲突,作者认为,当前的系统并没有仔细考虑作者和ReaveReS2中的社会张力。STG可以帮忙!为了找到社会脆弱子图(STG)3,STG的细长需要被适当地建模。因此,我们引入K三角的概念作为测量STG的细长的基础。当三个个体位于K跳之间时,存在一个社会网络中的K三角。在下面,我们首先对K三角进行了形式化定义,然后讨论了它的性质和优点。
定义1.1:一个K三角形是顶点{u,v,w
}的三重态,使得dG(u,v)小于k,dg(u,w)为k,dg(v,w)为k,其中dg(x,y)是G上两个顶点x,y之间的最短路径距离(跳变)。
值得澄清的是,对于子图F中的k-三角{u,v,w },在每一对顶点之间的最短路径距离在整个图形g上计算而不是f,因为所选成员的社会关系超出F。例如,考虑图1(a)中的f= {v1,v3,v6}。F从VF1到TV3上的最短路径距离是无穷大的,但它是2乘。
三角形作为测量网络中顶点邻域之间的各种密度关系的基本单元,例如聚类系数、传递率和K桁架。考虑到这个因素,一个组里k三角形越少,组就越稀疏。事实上,(k-1)三角形是一个k三角。如果一组没有k三角形,则它没有任何(k-1)三角形,(k-2)-三角形,…,和1-三角形。事实上,如果一组没有任何k三角形,则不包含任何|H|≥3以上的子图H,其中所有的v ∈ H4有dG(u,v)≤k。因此,K三角的计数对于测量群的稀疏度非常有用。
注意K三角在测量群的稀疏度方面有很大的优势。首先,K三角捕获到K跳的社会关系。两个拥有更多普通朋友的独立个体在k跳内(k hops)有更多的K-三角形。以图1(c)为例。F2= {V2,V4,V7,V8}中没有三角形(没有1-三角形),但存在四个两个三角形,即每对顶点有一个共同的朋友。相反,在图1(d)中,F3={V1,V2,V6,V8},其不具有2-三角形,比F2更加稀疏。第二,K-三角形作为许多其他图形结构的基本块,如路径、树、星甚至团。考虑图1中的示例。路径{V1,V7,V3}是一个2-三角形,而{V3,V4,V7,V8}(一个以V4为根的树以及以V3为中心的星形)包含四个2个三角形。此外,每个大小p的团包含精确的Cp3三角形。如果在子图中k三角的数目最小化,
2.事实上,有些人认为,双盲审查可能并不真正盲目,因为研究团体很小。有时在论文招标阶段不难猜出作者的身份。 3、在社会背景下,本文在社会背景下交替使用。
4对于H=2的情况,我们可以通过人工路径将虚拟的点q链接添加到组中的每个顶点。通过控制人工路径的跳数,可以将原始组中的K三角变换为消除H=2的子图H。
上面提到的图形结构(其密度的密集度)也被有效地最小化。在本文中,我们提出了一个新的研究问题,即最小k-三角形断开群(MKTG),它通过优化组的稀疏度找到一个STG -最小化由组大小归一化的K三角的数目。给定一个社会网络G=(V,E),MKTG从G中找到一组F,每个顶点的最小数量的K三角形服从以下约束。1)F包含不少于n的个体(大小约束)。2)F中没有边(没有配对约束)。根据实际需要,可以确定至少三个审稿人。非配对约束保证F不包含任何自我朋友(直接连接的朋友),这对于形成心理教育组和寻找论文评审者也是重要的。请注意,即使F没有直接连接的朋友,F仍然可以包含很多k三角形(k=2)。例如,在图1(c)中,f2= {v2,v4,v7,v8}不包含边。然而,在F2中有四个2个三角形。
MKTG问题是不容易的,这是由于纠缠组大小约束、无对偶约束和社会细度客观函数而引起的。我们证明了MKTG问题是NP-难的,在任何比率内都是不可约的。经过深入分析,系统地解决了MKTG问题。针对一般图上的MKTG问题,提出了一种高效、有效的算法,即三角形和边减算法(TERA)。此外,我们设计了先进的处理策略TARA,即TRAA与先进的处理策略(TRA-ADV),它结合了图论策略,即单纯修剪和邻域划分和消除,以显著避免在图中检查冗余度。然后,在阈值图[31]中讨论MkTTG问题。我们特别关注阈值图,因为许多流行的在线社交网络的结构特性(例如,度分布、最大分量大小、边缘密度和局部聚类系数)与阈值图相似[32]。我们提出了一种基于邻近预序概念的最优时间求解算法。
其贡献概括如下。
我们发现了一个在在线社交网络中寻找脆弱群体的新问题,并引入了一个新的K三角概念来测量群体的纤度。相应地,我们构造了最小k-三角形断开群(MKTG)问题,证明了它在任何比率下都是NP-难的和不可逼近的。
对于一般图中的MKTG,我们设计了两种算法,即三角和边消除算法(TERA),以及先进的处理策略(TRA-ADV)。后者采用基于图论的简单修剪和邻域划分和消除方法,有效且有效地求解。
我们研究了一类特殊的图中的MKTG问题,即阈值图,它的图形性质与许多著名的在线社交网络非常相似。我们表明,我们提出的算法可以获得最佳的解决方案多项式时间根据概念的前序。
我们对实际数据集进行了广泛的实验,以评估所提出的算法和不同的基线。实验结果表明,我们的算法优于基线在解决方案的质量和效率。
论文的结构如下:第2节规定了MKTG问题。第3部分介绍了与本文相关的工作。第4和5节分别给出了一般图和阈值图上的MKTG算法。第6节给出了实验结果,第7部分结束了本文。
2 问题的定义和难度
给定一个社会网络G=(V,E),让|F|表示F中的顶点数,而∆k(F)表示F中的k-三角形的数目。
问题:最小k-三角形断开群(MKTG)。
给出:一个社会网络G=(V,E),大小约束n,和最小参数k:
找到:一个子图F包含于G(F ⊆ G),其中|F| ≥ n(大小约束)和∄u,v ∈ F 有边(u,v)∈E(无对约束),使得 最小化。
当群大小|F|(或大小约束n)增加时,最小化K-三角的数目就变得越来越难,并且更倾向于违反无对偶约束。因此,该组的目标函数包括标准化TMM5,以鼓励不同大小的探索组,而不是总是尝试最小的组(即|F|=n)。直观地,上述的细度目标旨在最小化组中每个成员的平均数量三角形。因此,MKTG面临的挑战之一是在F中的群大小|F|(或大小约束n)与k-三角形的数目之间取得良好的平衡;另一方面,细度参数K对k-三角的数目也有重要影响。当k增加时,找到一个具有少量的K三角的子图变得更加具有挑战性,因为k跳朋友的数量对每个顶点都增加了。
MkTG的一种方法是首先构造K跳图(详见后面),Gk,然后构造Gk的补图 ,并使用现有的算法从b Gk中提取稠密子图。具体来说,给定输入图G =(V,E)和参数k,k跳图Gk =(V,Ek)保留顶点集合V并将边集合E扩充为Ek。当且仅当u和v在G上的k跳内,即dG(u,v)≤k时,存在边(u,v)∈Ek。通过将G转换为Gk,我们确保当且仅当{u,v,w}是Gk中的一个三角形时,G中存在一个k-三角形{u,v,w}。然而,由于k-三角形和无对约束的相互作用,在b Gk上找到稠密子图不能获得MkTG的良好解。
图2给出了上述方法的一个反例。给定图2(a)中的G和一个k = 2,n = 3的MkTG,图2(b)是两跳图,即G2和且图2(c)是G2的补充图,即 。这个MkTG实例在G上的一个最优解是{v1,v2,v5},没有满足非对约束的2个三角形。相反,如果我们使用该算法在G2的补图上找到具有最大密度的子图Fd(即最大化 )。
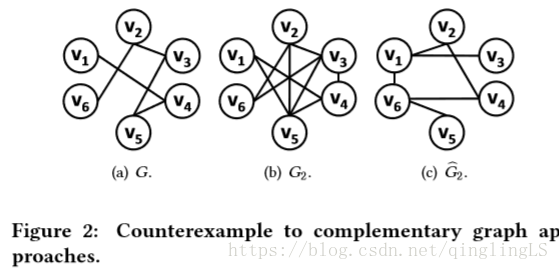
在图2(c)中,我们有Fd = {v1,v2,v3,v4,v6},其中 = 1.然而,在原始图G上的Fd中存在2-三角形({v2,v3,v6}),并且Fd不满足无对约束。这个例子表明MkTG是非常具有挑战性的,直接的方法不能很好地解决它。
所提出的MkTG问题是NP困难的,并且在任何比例内都不可接近,这可以通过从最大独立集(MIS)问题(我们在[10]中提出硬度分析)引入间隙来证明。因此,在任意图中设计MkTG的任意有限比的近似算法是不可能的。然而,仔细分析问题后,我们观察到对于重要的图类,即阈值图[31],仍然有可能在多项式时间内获得MkTG问题的最优解。我们对MkTG的阈值图特别感兴趣,因为它们与许多现实生活中的社交网络相对应。例如,据最近的一项研究[32]报道,群际网络与社会网络(如LiveJournal,Flickr,Youtube)的结构特性(包括度分布,最大分量大小,边缘密度和局部聚类系数)与阈值图的结构。因此,我们还分析了阈值图上的MKTG问题。
3.相关的工作
提取密集子图或社区是一个重要的研究课题,具有很多社会应用。为了找到稠密子图,例如直径[8],密度[11],集团及其变化[12],已经提出了各种各样的社会凝聚措施。此外,社区检测方法已被积极研究以从社交网络中提取密集连接的子图[13,14],而基于现有朋友之间的紧密程度和其他关键因素组织社交群体的研究[15-17]也已被研究。 GSGQ [15]和MRGQ [16]提取了具有空间约束的社会密集组,同时也检验了用户偏好[17]。虽然上述研究涵盖了各种应用,但他们专注于从在线社交网络中提取密集的子图。相比之下,本文探讨了寻找k-三角形数量最少的子图的一个新问题。因此,先前工作中的算法不能应用于MkTG问题。
最近的一系列研究集中在图形稀疏化,简化,稀疏的扳手和大规模网络采样[18-22]。这些算法旨在找到简洁和具有代表性的子图,并保留基本的图属性以便结果仍然能对网路工作分析有效。
例如,DEDS [18]将原始图形处理成多个较小的网络,以提高链接预测的效率,而网络的结构被简化为聚类[19]。相反,MkTG不会提取保留图属性的子图。它旨在找到具有最小数目的k-三角形的相互远离的顶点的子集。一些理论着作分析了无三角形图[23-26]。在[23]中研究了无三角形图中的独立集的数目,而在[24,25]中提出了五角形无三角形的图。不过,值得注意的是,无三角图无法确保互相影响。即使子图F不包含三角形,F的成员仍然可以在社交上彼此接近,例如朋友的朋友。最重要的是,上述作品着重于分析无三角形图的属性,但显然在线社交网络不是三角形的。一些理论着作[27-29]也分析了其他稀疏图的性质,例如弦图,区间图和完美图[27,29]。尽管如此,上述研究并不旨在从社交网络中提取子图。
4.在一般图上的MkTG
在本节中,我们提出了两种新算法,即三角形和边缘归约算法(TERA)和带有高级处理策略的TERA(TERA-ADV),以便有效地寻找通用图上的MkTG问题的货物解决方案。虽然它在第2节所示的任何比例内都不可比,但我们稍后会在第5节中证明,所提议的TERA可以在多项式时间内找到MkTG的最优解,该阈值图与许多在线社交网络具有相似的性质。
为了解决MkTG,需要仔细检查几个关键因素。第一个因素是tenuity目标及其与无对约束的相互作用,即F中必须不存在边。为了最小化k-三角形的数量,一种贪心策略是迭代地选择几个三角形中涉及的顶点。然而,这些顶点可能共享共同的入射边缘,因此无法确保无配对约束。第二个因素是最小组大小n和k-三角形数量之间的折衷。目标函数旨在最小化F中的平均k-三角形数量,即最小化 。随着k和n的增加,在F中更有可能具有k-三角形。因此,如何在组合大小和ktriangles数量之间取得平衡对于最小化客观价值至关重要。
为了解决上述因素,我们在算法设计中考虑了三个思想:1)包含孤立顶点,因为孤立顶点确保双对约束和k-三角形数目的最小化。然而,仅仅依靠孤立的顶点是不实际的,因为孤立顶点的数量通常很小,特别是在在线社交网络中。 2)识别出现在许多k-三角形中的顶点。如果这些顶点被识别并从结果组F中移除,则可以显着减少k-三角形的数量。请注意,F中的很多k-三角形不一定涉及具有较大程度的顶点,因为不是所有相邻顶点都总是在F中选择。3)为了生成多个不同大小的候选组以便提取组大小和k-三角形数量之间的最佳平衡点。
下面,我们首先介绍4.1节中的基本TERA,然后使用4.2节中的高级预处理和修剪技术来加强它。所提出的高级技术可以离线预处理社交网络以支持用户在线发布的MkTG中的任意参数k和n。
4.1三角形和边缘减少算法
在TERA中,我们首先为每个顶点v分配一个权重w(v),其中w(v)是k个三角形v参与的数量。注意,这个步骤可以通过将G转换成khop图Gk (如第2节所述)6,然后指定每个顶点参与Gk asw(v)的三角形数量。 然后,给定运行时参数k和n,TERA迭代地从G中去除具有最大顶点权重的顶点vi(及其入射边)。 更具体地说,letHi + 1 denotethegraphafter在迭代i中从Hi中移除顶点vi。 最初,H1被设置为G.在之后的每次迭代中,Hi + 1表示图Hi - {vi}。

直觉是删除大量k-三角形中涉及的顶点可能会减少ktriangles的数量并在其余图中保留孤立的顶点。 因此,在第i次迭代中选择的vi是在Hi中具有最大w(v)的顶点,即,引起最大数量的k-三角形的剩余顶点。 请注意,度数越大的顶点越可能违反无对约束。 因此,如果在相同数量的k-三角形中存在多个转角,则我们优先选择具有较大程度的顶点在H上的诱导子图。 因此,Hi + 1是通过从Hi去除vi和其相应的边而生成的。 之后,在下一次迭代i + 1中处理Hi + 1。 以上程序在| Hi |时发生 ≤n。 最后,我们将满足无对约束的最小目标值的图H *∈{H1,H2,…}提取为输出解。
6.对于大多数网络来说,它们的k跳图成为k≥6的完整图。因此,我们只需要考虑2≤k≤5的k跳图。为了减少空间消耗,我们只存储一个顶点集拷贝 K跳图。 k跳跃图中的每个边e用k表示e时出现的整数ke标记。
值得注意的是,正如在困难分析中所证明的那样,决定MkTG是否有任何可行的解决方案,遵循无对约束是NP-Complete。因此,当MkTG实例不包含任何可行的解决方案时(否则,P = NP成立),TERA和任何其他算法可能无法找到可行解。
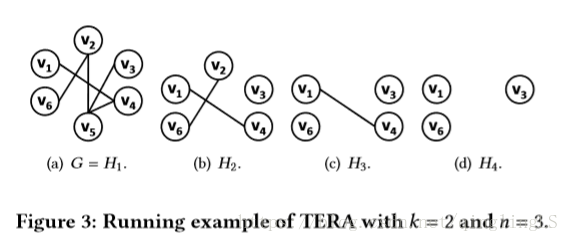
例4.1:图3是k = 2和n = 3的TERA示例。TERA以H1 = G开始(图3(a))。由于v5涉及2个三角形的最大数量,v5从H1中移除并产生H2(图3(b))。然后,从H2中移除v2以创建H3(图3(c))。最后,我们移除v4和H4 = {v1,v3,v6}。在所有的Hi中,H4的目标值是最小的,即0,并且H4满足非对约束。因此,H4由TERA返回。
TERA的时间复杂性分析。给定输入参数k和n,TERA移除每次迭代i中的vi和它的依附边,这需要O(δG)时间,其中δG是G中的最大度数。计算通过去除vi减少的k-三角形的数量取 时间。由于最多有O(|V|)次迭代,总体时间复杂度为 .
4.2高级策略TERA
通过对TERA的分析和评估,我们观察到,没有必要检查G中的整个顶点集,因为许多顶点永远不会满足无对约束。此外,许多顶点是多余的,可以从G中移除,因为这些顶点总是可以被替换以降低目标值。因此,我们通过研究上述观察提出了TERA的高级版本,即TERA-ADV。 TERA-ADV包含两个主要观点:1)预先剪枝策略,即Simplicial Pruning(SP),它显着减少了TERA开始之前设置的顶点的大小。 2)根据图论将顶点集划分为若干个组件,并设计一个策略,即邻接分区和消除策略(VPE),以消除TERA中的冗余检查。传统的修剪策略通常在运行时执行。相比之下,在任何查询到达之前,任何问题实例中的任意k和n都可以离线执行Simplicial Pruning和Vicinal Partition and Elimination。通过消除大量冗余顶点,这些策略可以显著降低图的在线计算成本和存储成本。令GSP和Gν分别为SP和VPE后的图。
7.另一种方法是通过用Δk(F)+ E(F)| F |来代替F的微观目标,将解决方案中的边数增加到目标函数中。 其中E(F)是F中的边的数量.TERA可以通过包括在预处理步骤期间链接到k跳图Gk中的每个顶点的一组虚拟节点R来解决上述问题。 在这种情况下,如果有两个verticesu,v∈F共享边,则边将包含在| R |中 k-三角形,并且因此k-三角形的数量增加。 因此,最小化这个新的目标函数将阻止F包含边缘。
简单修剪(SP)。给定一个图G =(V,E)和一个顶点x∈V,令N(x)表示x的一跳邻居,并设N [x]表示x的闭边邻居,即N [x] = N(X)∪{X}。例如,图4(a)中的N [v1] = {v1,v3,v9}。简单顶点s∈V是N(s)形成一个集团的顶点。例如,v1,v2,v10是单纯的顶点。简单顶点具有很好的属性,因此在提出的简单修剪策略中发挥重要作用。
对于单纯顶点的第一个好性质,给定MkTG问题和单纯顶点s的可行解H(即满足无对约束),最多一个顶点与H和N [s]重叠。
引理4.2。给定一个可行解H和单纯顶点s,|H∩N[s] | ≤1成立。
证明。由于s是一个单纯形顶点,并且N(s)形成一个集合,(x,y)∈E,对于任意x,y∈N [s]。如果H中包含多个N [s]中的顶点,则H必须至少有一个边,并且H不是一个可行的解决方案。
因此,为了避免复杂的顶点,我们可以选择N [s]中的顶点并修剪其他顶点,因为N [s]中至多有一个顶点会出现在任何可行的解决方案中,以确保无对约束。然而,所选顶点的真实性并不明显。因此,单纯顶点的第二好性质表明,我们总是可以选择单纯顶点本身(并修剪N [s]中的所有其他顶点),它必须满足无对约束并生成最小目标值。
引理4.3。给定一个可行的解H和一个单纯的顶点s,如果y =H∩N[s]和H’= H- {y}∪{s},那么H’不会比H更坏。
……
排版实在是太麻烦了 ,完全版自己点下面的链接下载,是word通用版本
https://download.csdn.net/download/qinglingls/10512206
大约15000个子,耗时三日,花了12小时,一积分辛苦积分,谢谢各位啦!
