SMO算法--SVM(3)
利用SMO算法解决这个问题:
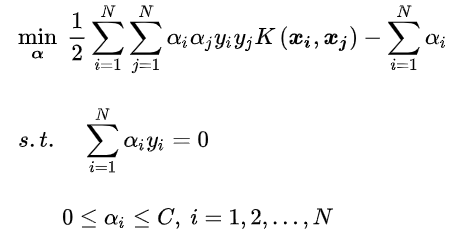
SMO算法的基本思路:
SMO算法是一种启发式的算法(别管启发式这个术语, 感兴趣可了解), 如果所有变量的解都满足最优化的KKT条件, 那么最优化问题就得到了。
每次只优化两个 , 将问题转化成很多个二次规划的子问题, 直到所有的解都满足KKT条件为止。
, 将问题转化成很多个二次规划的子问题, 直到所有的解都满足KKT条件为止。
整个SMO算法包括两个部分:
1, 求解两个变量的解析方法
2, 选择变量的启发式方法
## 求解两个变量的解析方法
先选择两个变量,其余的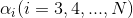固定, 得到子问题:
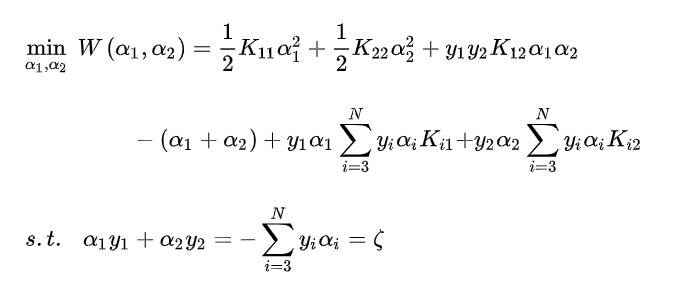
更新
先不考虑约束条件, 代入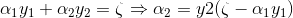 , 得到:
, 得到:
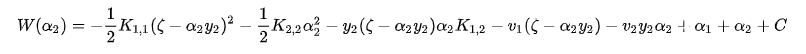
对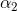 求导, 得到:
求导, 得到:
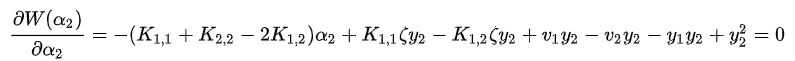
由于决策函数为:
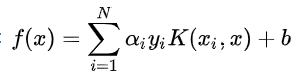
令:

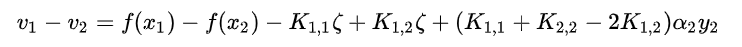
定义**误差项**:
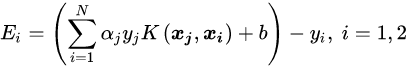
定义学习率:
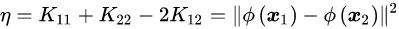
将v1, v2代入到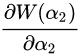 中, 得到:
中, 得到:
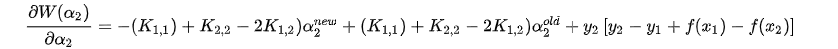
代入误差项和学习率, 得到最终的导数表达式:
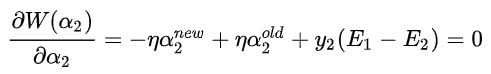
求出:
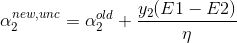
表示未加约束条件求出来的(未剪辑)
加上约束条件:
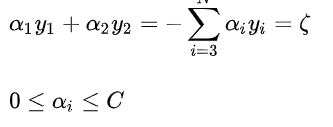
约束条件如下图的正方形框所示, 一共会有两种情况:

以左图为例子分析: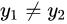,约束条件可以写成: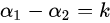,分别求取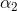的上界和下界:
下界: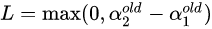
上界: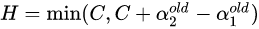
同理,右图情况下
下界: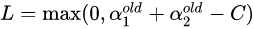
上界: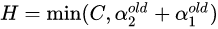
加入约束条件后:
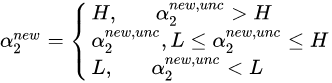
然后根据: 计算出
计算出 :
:
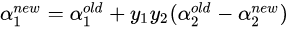
## 选择变量的启发式方法
 的选择
的选择
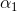 选择违反KKT条件的,
选择违反KKT条件的, 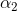 选择使|E1 - E2|变化最大的。
选择使|E1 - E2|变化最大的。
具体过程如下:
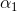 的选择:
的选择:
由KKT条件:
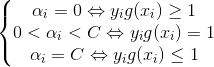
具体证明过程:
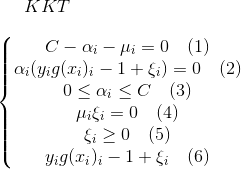
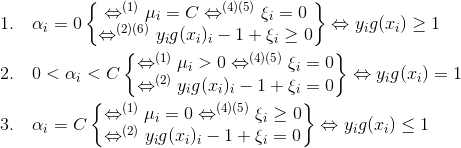
一般来说,我们首先选择违反 这个条件的点。如果这些支持向量都满足KKT条件,再选择违反
这个条件的点。如果这些支持向量都满足KKT条件,再选择违反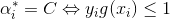 和
和 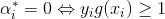 的点。
的点。
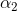 的选择:
的选择:
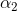 要让|E1 - E2|变化最大。E1已经确定, 找到使得|E1-E2|最大的E2对应的
要让|E1 - E2|变化最大。E1已经确定, 找到使得|E1-E2|最大的E2对应的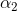 即可。
即可。
更新 b
更新b要满足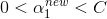 :
:
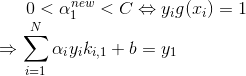
得到:
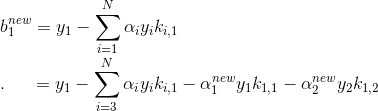
根据E1的计算公式:

代入即可得到:
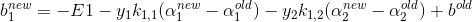
同理:
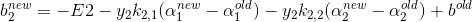
更新b:
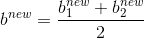
更新Ei
更新Ei时候, 只需要用到支持向量就好了, 因为超平面就是用支持向量来确定的, 其他的点其实并没有贡献什么作用, 只计算支持向量可以减小计算量。

其中,S是支持向量的集合。
## SMO算法的总结:
先初始化参数, 选择, 然后更新到所有变量满足KKT条件。
.

.

.
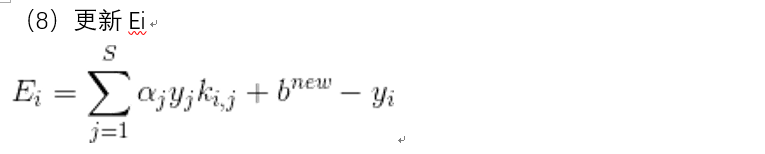
 , 将问题转化成很多个二次规划的子问题, 直到所有的解都满足KKT条件为止。
, 将问题转化成很多个二次规划的子问题, 直到所有的解都满足KKT条件为止。
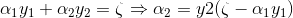 , 得到:
, 得到: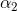 求导, 得到:
求导, 得到: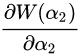 中, 得到:
中, 得到: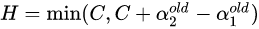
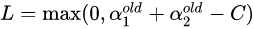
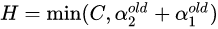
 计算出
计算出 :
: 的选择
的选择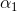 选择违反KKT条件的,
选择违反KKT条件的, 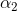 选择使|E1 - E2|变化最大的。
选择使|E1 - E2|变化最大的。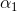 的选择:
的选择: 这个条件的点。如果这些支持向量都满足KKT条件,再选择违反
这个条件的点。如果这些支持向量都满足KKT条件,再选择违反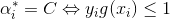 和
和 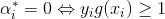 的点。
的点。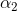 的选择:
的选择: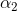 要让|E1 - E2|变化最大。E1已经确定, 找到使得|E1-E2|最大的E2对应的
要让|E1 - E2|变化最大。E1已经确定, 找到使得|E1-E2|最大的E2对应的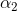 即可。
即可。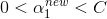 :
: