排序

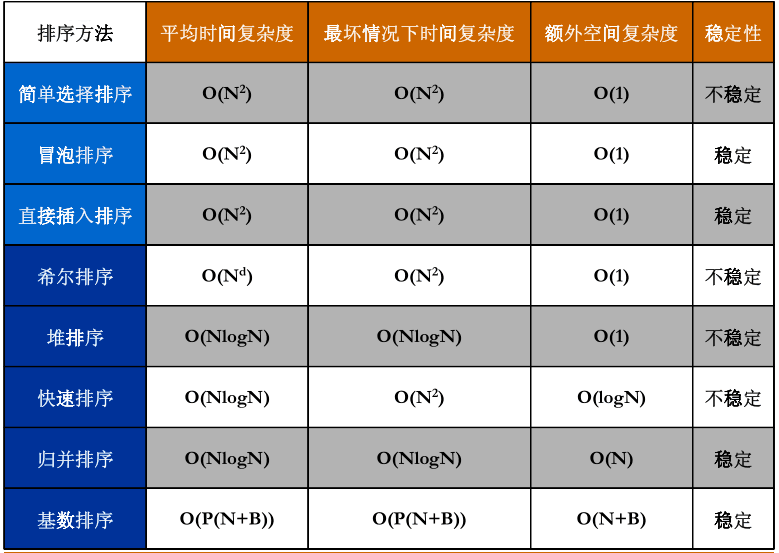
简单排序（前三种就是简单排序）
void X_sort(ElementType A[ ], int N)
1.大多数情况下，为简单期间，讨论从小到大的整数排序
2.N是正整数
3.只讨论基于比较的排序（> = <有定义）
4.只讨论内部排序
5.稳定性：任意两个相等的数据，排序前后的相对位置不发生改变
6.没有一种排序是任何情况下都是变现最好的

1.冒泡排序

void Bubble_sort(ElementType A[], int N)
{
    int flag, i, j;
    for (i = N - 1; i >= 0; i--)        //N- 1趟冒泡
    {
        flag = 0;
        for (j = 0; j < i; j++)
        {
            if (A[j] > A[j + 1])
            {
                swap(&A[j], &A[j + 1]);
                flag = 1;                //标识发生了交换
            }
        }
        if (flag == 0) break;        //全称无交换
    }
}

或者是

void Bubble_sort(ElementType A[], int N)
{
    int flag, i, j;
    for (i = 0; i < N - 1; i++)
    for (j = 0; j < N - i - 1; j++)
    {
        if (A[j] > A[j + 1])
            swap(&A[j], &A[j + 1]);
    }

}

算法复杂度：
最好情况：顺序 T = O(N)
最坏情况：逆序 T = O(N^2)

2.插入排序

void Insertion_Sort(ElementType A[], int N)
{
    int i, j;
    ElementType tmp;
    for (i = 1; i < N; i++)
    {
        tmp = A[i];
        for (j = i; j > 0 && A[j - 1] > tmp; j--)
            A[j] = A[j - 1];
        A[j] = tmp;
    }
}

3.选择排序

void _Sort(ElementType A[], int N)
{
    int i, k, j;
    for (i = 0; i < N - 1; i++)
    {
        k = i;
        for (j = i; j < N; j++)
        {
            if (A[k]> A[j])
                k = j;
        }
        swap(&A[k], &A[i]);
    }
}

4.希尔排序：如果增量元素不互质，则小增量可能根本不起作用，则增量的选取可以采用Hibbard或Sedgewick增量序列

void Shell_sort(ElementType A[], int N)
{
    int i, j, increament;
    ElementType temp;
    for (increament = N / 2; increament > 0; increament /= 2)
    {
        for (i = increament; i < N; i++)
        {
            temp = A[i];
            for (j = i; j >= increament; j -= increament)
            {
                if (A[j - increament] > temp)
                    A[j] = A[j - increament];
                else
                    break;
            }

            A[j] = temp;
        }
    }
}

或：

void Shell_sort(ElementType A[], int N)
{
    int i, j, increament;
    ElementType temp;
    for (increament = N / 2; increament > 0; increament /= 2)
    {
        for (i = increament; i < N; i++)
        {
            temp = A[i];
            for (j = i; j >= increament && A[j - increament] > temp; j -= increament)
                A[j] = A[j - increament];
            A[j] = temp;
        }
    }
}

5.堆排序：
//将树调整成最大堆

void PercDown(ElementType A[], int i, int N)
{
    int child;
    ElementType temp;
    for (temp = A[i]; (2 * i + 1) < N; i = child)
    {
        child = 2 * i + 1;
        if (child != N - 1 && A[child] < A[child + 1])
            child++;
        if (temp > A[child])
            break;
        else
            A[i] = A[child];
    }
    A[i] = temp;
}

void Heap_sort(ElementType A[], int N)
{
    int i;
    for (i = N / 2; i >= 0; i--)        //BuildHeap
        PercDown(A, i, N);
    for (i = 0; i < N - 1; i++)            //DeleteMax
    {
        swap(&A[0], &A[N - 1 - i]);
        PercDown(A, 0, N - i - 1);
    }
}

DeleteMax还可以写成这样
for (i = N - 1; i > 0; i--)            //DeleteMax
    {
        swap(&A[0], &A[i]);
        PercDown(A, 0, i);
    }

6.1归并排序(递归实现）

//Left = strart of left half, Right = start of right half, RightEnd = end of right half
void Merge(ElementType A[], ElementType TmpArray[],
    int Left, int Right, int RightEnd)
{
    int LeftEnd, SumNum, temp, i;
    temp = Left;
    LeftEnd = Right - 1;
    SumNum = RightEnd - Left + 1;

    //main loop
    while (Left <= LeftEnd && Right <= RightEnd)        
    {
        if (A[Left] < A[Right])
            TmpArray[temp++] = A[Left++];
        else
            TmpArray[temp++] = A[Right++];
    }
    while (Left <= LeftEnd)                //copy rest of first half
        TmpArray[temp++] = A[Left++];
    while (Right <= RightEnd)            //copy rest of second half
        TmpArray[temp++] = A[Right++];    

    for (i = 0; i < SumNum; i++, RightEnd--)        //copy TempArray back
        A[RightEnd] = TmpArray[RightEnd];
}

void MSort(ElementType A[], ElementType TmpArray[],
    int Left, int Right)
{
    int Center;
    if (Left < Right)
    {
        Center = (Left + Right) / 2;
        MSort(A, TmpArray, Left, Center);
        MSort(A, TmpArray, Center + 1, Right);
        Merge(A, TmpArray, Left, Center + 1, Right);
    }
}

void Merge_sort(ElementType A[], int N)
{
    ElementType *TmpArray;
    TmpArray = (ElementType*)malloc(N * sizeof(ElementType));
    if (TmpArray != NULL)
    {
        MSort(A, TmpArray, 0, N - 1);
        free(TmpArray);
    }
    else
        printf("No space for tmpArray[ ]!!!
"); 
}

 T = T(N/2) + T(N/2) + O(N)  ----> T= O(NlogN);

6.2 归并排序（非递归实现）

//Left = strart of left half, Right = start of right half, RightEnd = end of right half
void Merge1(ElementType A[], ElementType TmpArray[],
    int Left, int Right, int RightEnd)
{
    int LeftEnd, SumNum, temp;
    temp = Left;
    LeftEnd = Right - 1;
    SumNum = RightEnd - Left + 1;

    //main loop
    while (Left <= LeftEnd && Right <= RightEnd)        
    {
        if (A[Left] < A[Right])
            TmpArray[temp++] = A[Left++];
        else
            TmpArray[temp++] = A[Right++];
    }
    while (Left <= LeftEnd)                //copy rest of first half
        TmpArray[temp++] = A[Left++];
    while (Right <= RightEnd)            //copy rest of second half
        TmpArray[temp++] = A[Right++];    
}

//非递归算法 length = 当前子序列长度， Merge1将A中的元素归并到TmpA
void Merge_pass(ElementType A[], ElementType TmpA[], int N, int length)
{
    int i, j;
    for (i = 0; i <= N - 2 * length; i += 2 *length)
        Merge1(A, TmpA, i, i + length, i + 2 * length - 1);
    if (i + length < N)        //归并最后两个子列
        Merge1(A, TmpA, i, i + length, N - 1);
    else
    for (j = i; j < N; j++)        //最后只剩一个元素
        TmpA[j] = A[j];
}

void Merge_sort(ElementType A[], int N)
{
    int length = 1;
    ElementType *TmpA;
    TmpA = (ElementType*)malloc(sizeof(ElementType) * N);
    if (TmpA != NULL)
    {
        while (length < N)
        {
            Merge_pass(A, TmpA, N, length);
            length *= 2;
            Merge_pass(TmpA, A, N, length);
            length *= 2;
        }
        free(TmpA);
    }
    else
        printf("Run out of memory!!!
");
}

7.快速排序（也是分而治之）
最好情况：每次正好中分 T = O(NlogN)
选主元：
1.随机rand()函数不便宜
2.取头、中、尾的中位数
在程序中定义一个cutoff的阈值。当递归的数据规模充分小，则停止递归，直接调用简单排序（录入插入排序）
//选取主元

ElementType Median3(ElementType A[], int Left, int Right)
{
    int Center = (Left + Right) / 2;
    if (A[Left] > A[Center])
        swap(&A[Left], &A[Center]);
    if (A[Left] > A[Right])
        swap(&A[Left], &A[Right]);
    if (A[Center] > A[Right])
        swap(&A[Center], &A[Right]);

    swap(&A[Center], &A[Right] - 1);    //将pivot藏到右边
    
    //只需要考虑A[Left + 1]……A[Right - 2]
    return A[Right - 1];    //返回pivot
}

void Quicksort(ElementType A[], int Left, int Right)
{
    int i, j;
    ElementType pivot;
    if (Cutoff <= Right - Left)
    {
        pivot = Median3(A, Left, Right);
        i = Left, j = Right - 1;
        for (;;)
        {
            while (A[++i] < pivot) {}
            while (A[--j] > pivot) {}
            if (i < j)
                swap(&A[i], &A[j]);
            else
                break;
        }
        swap(&A[i], &A[Right - 1]);
        Quicksort(A, Left, i - 1);
        Quicksort(A, i + 1, Right);
    }
    else
        Insertion_sort(A + Left, Right - Left + 1);
}


void Quick_sort(ElementType A[], int N)
{
    Quicksort(A, 0, N - 1);
}

8.表排序
需要排序的每个元素很庞大（例如：结构体）
间接排序：
定义一个指针数组作为“表”（table)

例如在表排序中用插入排序：

void table_sort(ElementType A[], int N)
{
    int i, j;
    int table[N];
    ElementType temp;
    for(i = 0; i < N; i++)
        table[i] = i;
    for (i = 1; i < N; i++)
    {
        temp = table[i];
        for (j = i; j > 0 && A[table[j - 1]] > temp; j--)
            table[j] = table[j - 1];
        table[j] = temp;
    }
}

9.物理排序
N个数字的排列由若干个独立的环组成

10.桶排序
T(N, M) = O(M + N)

11.基数排序
次位优先

排序算法的比较