线性回归:是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
梯度下降,http://www.cnblogs.com/hgl0417/p/5893930.html
最小二乘:
对于一般训练集:
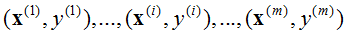
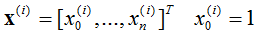
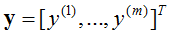
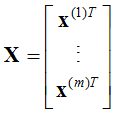
参数系统为:
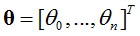
线性模型为:
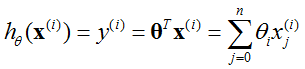
线性回归的目的为最小化损失函数J(θ),即:
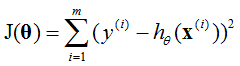
相关知识:Tr(A):矩阵A主对角线乘积。
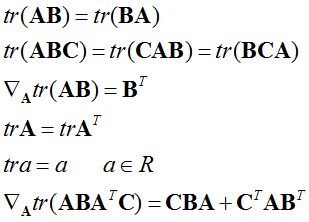
最小二乘的推导:(吴恩达)
由于
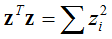
所以
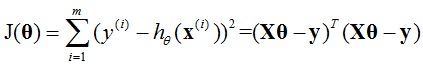
其中
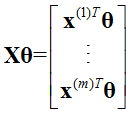
最小化损失函数J(θ)等价与一阶导数等于0,所以有
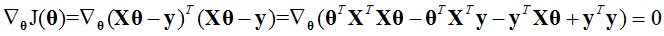
由于上式为实数
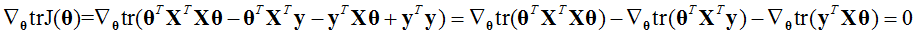
又因为
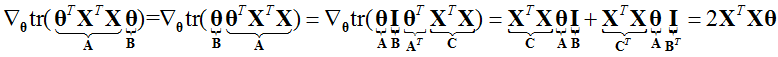
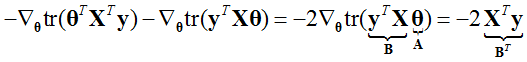
所以有:
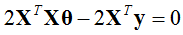
整理后,对于一般线性系统:
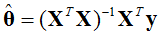
其中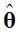 为θ的估计值
为θ的估计值
线性回归的概率解释(Probabilistic interpretaion)[1]:
假设:
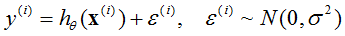
其中,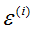 为误差(error),由许多原因引起,一般情况下服从正太分布(也有特殊情况,但是比较少见,引起误差的原因很多,每种原因相互独立,由中心极限可知,对于大多数问题,使用线性系统,尝试测量误差,误差一般服从正太分布,所以假设误差是正态分布是很好的假设)。所以:
为误差(error),由许多原因引起,一般情况下服从正太分布(也有特殊情况,但是比较少见,引起误差的原因很多,每种原因相互独立,由中心极限可知,对于大多数问题,使用线性系统,尝试测量误差,误差一般服从正太分布,所以假设误差是正态分布是很好的假设)。所以:
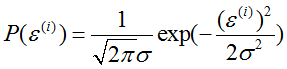
由于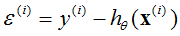 ,可以得到:
,可以得到:
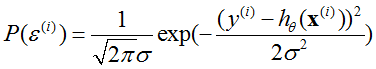
可以理解为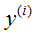 服从均值为
服从均值为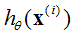 ,方差为
,方差为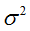 的正太分布,即
的正太分布,即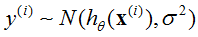 ,可以得到:
,可以得到:
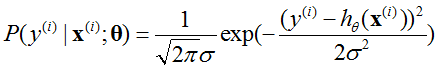
其中,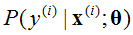 中不把θ作为随机变量。
中不把θ作为随机变量。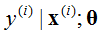 可以理解为
可以理解为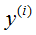 服从
服从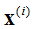 对于θ的高斯分布。
对于θ的高斯分布。
对于每一个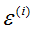 是独立同分布的(Independently Identically Dstributed, IID),所以有:
是独立同分布的(Independently Identically Dstributed, IID),所以有:
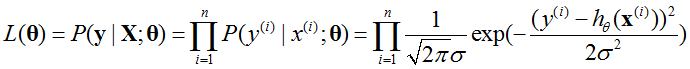
这里取值越贴近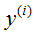 的概率越大,所以选择θ使L(θ)最大,为了数学上的便利,将L(θ)转换为log 的形式,因为log 的形式不改变L(θ)的单调性,所以有:
的概率越大,所以选择θ使L(θ)最大,为了数学上的便利,将L(θ)转换为log 的形式,因为log 的形式不改变L(θ)的单调性,所以有:
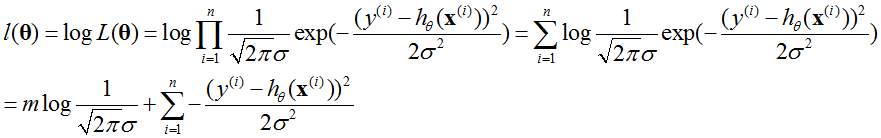
所以最大化l(θ)等价于最小化函数:
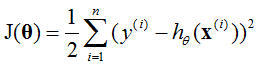
得到了线性回归的目标函数。
[1] 网易公开课——斯坦福大学机器学习
**转载请注明出处!