一. 前言
最近开始搞自动驾驶感知部分,将之前的总结的资料和笔记调出来看看,顺便总结一下,留下记录。
二. 神经网络介绍
这里我们采用优达学城[1]上提供的例子,如下图所示。
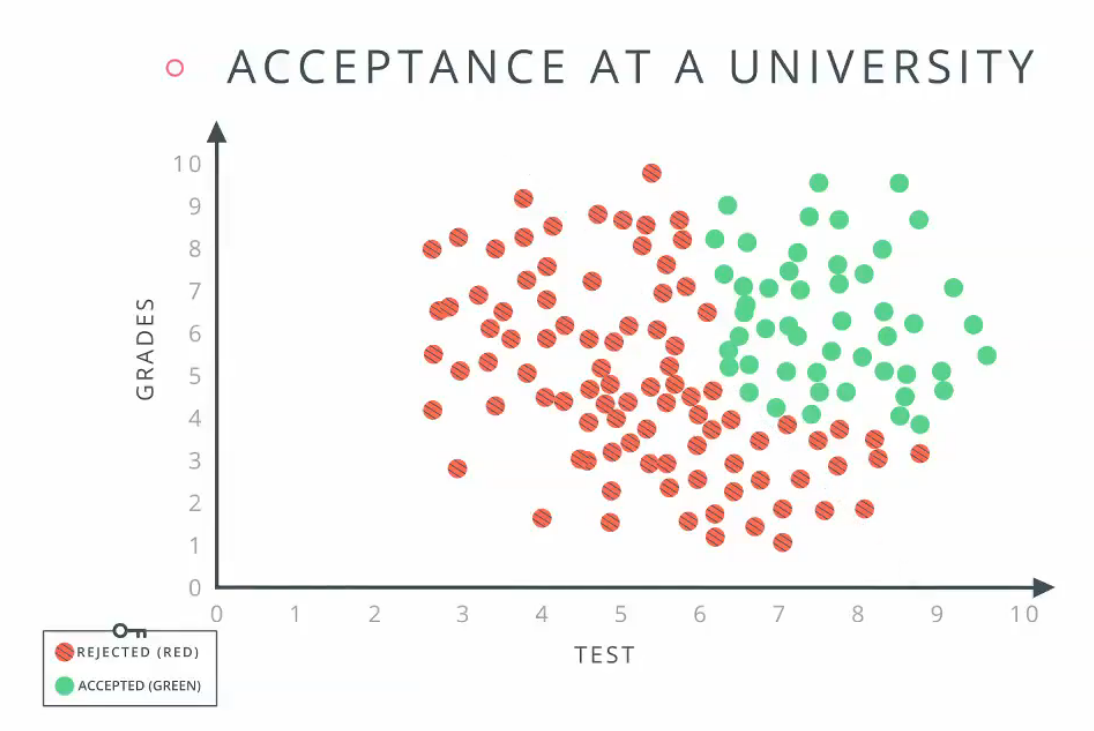

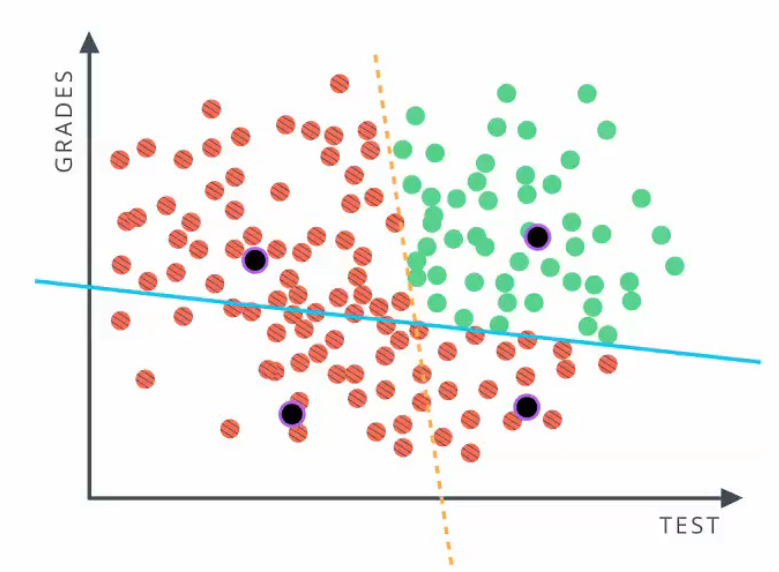
图 1-1 图 1-2 图 1-3
上图是根据grades和test的成绩来判断是否被大学录取,绿色的圆表示录取,红色的圆表示拒绝录取。
从上图1-1可以看出,如果采用线性的方法区分红色和绿色,采用一条直线直线的效果不好(图1-2),所以需要用两条直线区分(图1-3)。
例如,如果一个学成的test的成绩为1,grade的成绩为8,那么根据图1-3,该学生拒绝录取,即,该学生的成绩在蓝色线的上方,但却在黄色线的左侧,所以拒绝录取,可以如图2表示

图 2
这里我们总结一下所有录取和拒绝录取的情况,根据图1-3可以分为四种情况,如下表
表1
| test在黄线右侧 | grade在蓝线上方 | 结果 |
| 真 | 真 | 录取 |
| 真 | 假 | 拒绝 |
| 假 | 真 | 拒绝 |
| 假 | 假 | 拒绝 |
通过表1可以看出,图2是“AND”(“与”)的关系。图2就是一个简单神经网络。
根据不同的场景,最后的关系可以是“OR”,“XOR”,甚至可以自定义逻辑关系等等。
那么我们怎样判断test在黄线的右侧,grade在蓝线的上方呢?实际上就是我们接下来要聊的神经元(感知机)
三. 感知机
图2中, 中间的两个方框中的节点实际上就是感知机(神经元),他们构成了神经网络的基本单元,每个感知机按照输入决定数据的分类。
那么,感知机是如何决定test在黄线的右侧,grade在蓝线的上方呢?事实上初始神经网络吧并不知道输入的test,或者grade在什么位置,即并不清楚图1-3的蓝线与黄线的位置,需要我们根据数据做出调整,这个过程就是“训练”。
训练神经网络的过程,实际上就是在确定蓝线与黄线的位置。
直线的方程在二维坐标系下可以写成:0 = w1 × x1 + w2 × x2 + b, 如果给出的x1与x2在直线的上方/右侧(上方与右侧等价),那么w1 × x1 + w2 × x2 + b > 0,否则<0。这里w1, w2, b就是神经网络中常用的权重,x1与x2分别代表图2中的test与grade数据。通过不停的带入test与grade数据,调整w1, w2, b训练整个神经网络。
图2的两个感知机都包含了0 = w1 × x1 + w2 × x2 + b的一个线性方程。
图2是针对二维坐标系的例子,如果是n维数据,那么可以写成和函数(summing function):
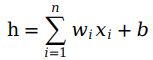
最后感知机要把和函数转换成输出信号,这里即1与0(“真”与“假”)。通常通过激活函数(activation function)实现。常用到的激活函数
我们常用的激活函数有:
(1)单位阶跃函数:和函数小于 0,函数返回 0,如果和函数等于或者大于 0,函数返回 1。
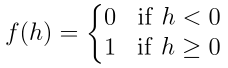
(2)sigmoid函数[2]

(3)tanh函数
(4)softmax函数[3]
我们常采用sigmoid函数作为激活函数。
这样我们就得到了我们简单的感知机模型,如下图所示:

这里我们解决了神经网络每个节点的构成,接下来我们着重介绍,神经网络的训练方法,也就是权重的学习。
四. 权重调整
因为神经网络的初始随机权重不能满足我们的需求,所以我们需要通过正确的数据不断调整我们网络中的权重,这个过程就是训练。
目前训练采用的主流方法就是梯度下降,权重调整的目的是使目标函数的输出,趋近于真值。
4.1 目标函数
训练的目的就是通过带入真实数据调整权重,使输出趋近于真值。所以为了能够衡量,我们需要有一个指标来了解预测与实际的差别,也就是误差(真值与计算结果的差异)。一个普遍的指标是误差平方和 sum of the squared errors (SSE)
举例一个单个感知机来解释(以下的推导过程都是基于单个感知机):
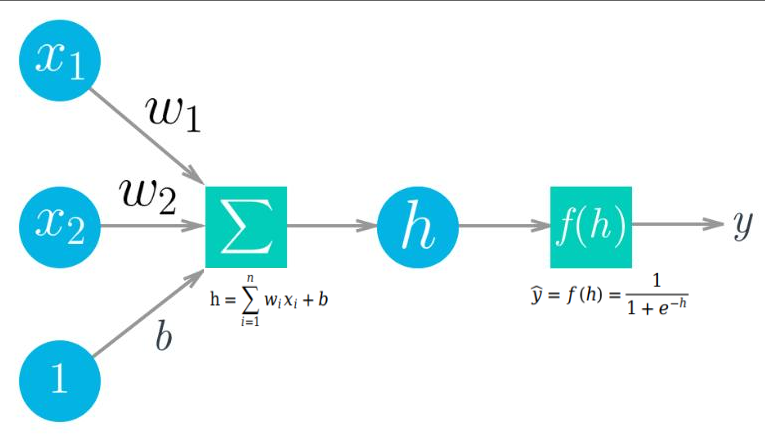
图3
ŷ表示感知机输出,y表示真值。
首先,我们想知道我们初始的感知机的输出与真值之间的误差,希望误差全部为正,便于累加,误差可以表示为
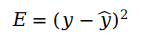
※※不采用绝对值的原因是,对于较大的误差可以通过平方放大其误差,从而带来放大惩罚值,同时采用平方的形式有利于我们后面的数学运算(求导)。
上面的E仅仅代表了单个数据的误差,如果我们想要得到整体数据的误差,可以所有误差进行累计,即
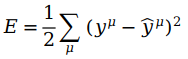
每一行的x和y的对应元素代表μ(x,y的上角标)。我们得到了整体数据的误差E,即误差平方和 (SSE)。ŷ是由激活函数得到,1/2方便计算导数,μ用于表示整体数据。比如
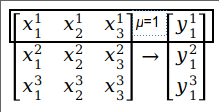
这样针对权重wi 的优化目标函数E已经得到。从上式可以看出,E取决于权重wi 与输入 xiμ。如果E的值比较大,那么预测的结果比较差,如果E较小,那么预测的结果会比较好。所以我们希望E越小越好。
这时我们要优化的所有函数可以表示为
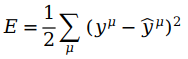
其中
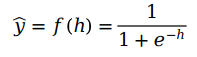
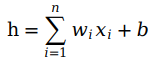
4.2 梯度下降[4]
针对4.1节中提到的优化函数方法有很多,我们这里着重讲解梯度下降。实际上不需要了解梯度下降的数学细节,知道结果就好,因为好多工具帮大家实现了梯度下降,而且包含了很多方法[4]。
由于初始的E比较大,我们希望E变得越来越小,而且变小的速度还要够快,所以我们利用导数,来计算梯度下降对快的方向,下降的方向与导数相反。我们只需每次累加梯度下降的方向。如图4所示
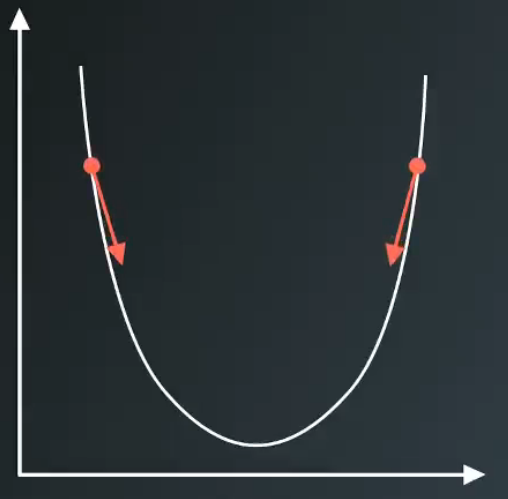
图4
梯度下降的方法有很多,这里选用随机梯度下降SGD[4]。由于随机梯度下降的核心:用样本中的一个例子来近似我所有的样本,调整权重,所以导数只需求解单个样本即可,不需要包含∑符号。针对4.1的目标函数,采用链式求导法则有
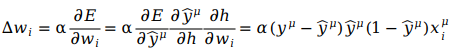
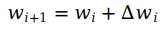
α为学习速率(learning rate),包含了方向(正负号),用来控制下降的速度。链式求导在下面要说到的反向传递也要用到,正因为有链式求导,神经网络的层数才可以增加,深度学习才可以方便调整参数。由于我们采用sigmoid函数作为激活函数f(h),sigmoid函数的导数为:f'(h) = f(h)(1 - f(h)) = ŷ(1 - ŷ)。
为了表达简单,迭代过程化简为:
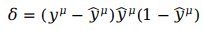
δ实际上表示误差项,即用于衡量输出的误差。
随机梯度下降SGD的过程pipeline表示为:
- 权重步长设定为 0:Δwi = 0 对训练数据中的每一个样本:
- 通过网络做正向传播,计算输出:ŷ = f(h)
- 计算输出单元的误差项:δ
- 更新权重步长:Δwi = Δwi + δxi更新输入对应权重
- 更新权重:wi+1 = wi + αδxi
- 重复上面迭代,直至迭代步数结束。
上面的阐述仅仅围绕着神经网络中一个节点进行,单层多节点的神经网络类似,但是多层神经网络(深度学习)要复杂一些,涉及到神经网络核心——反向传播。
4.3 反向传播
我们已了解了使用梯度下降来更新单个节点权重,反向传播算法则是它的一个延伸。用以更新多层神经网络的参数,反向传播同样基于链式求导法则,。
网络上有个一很不错的例子,我用这个例子[5]讲解一下反向传播。

这个神经网络有两个输出,一层隐含层(两个节点),两个输入。
第一层是输入层,包含两个神经元i1,i2,和截距项b1;第二层是隐含层,包含两个神经元h1,h2和截距项b2,第三层是输出o1,o2,每条线上标的wi是层与层之间连接的权重,激活函数同样使用sigmoid函数。
初始值为:
输入数据: i1=0.05, i2=0.10;
输出数据: o1=0.01, o2=0.99;
初始权重: w1=0.15, w2=0.20, w3=0.25, w4=0.30; w5=0.40, w6=0.45, w7=0.50, w8=0.55;
目标:给出输入数据i1, i2(0.05和0.10),使输出尽可能与原始输出o1, o2(0.01和0.99)接近
这里先列出了前向传播及目标函数的所有公式
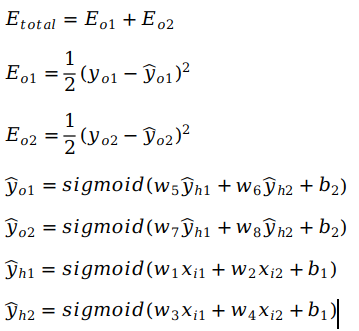
(上述公式建议从下往上看)其中,Etotal为总的误差,Eo1与Eo2分别为两个输出的误差SSE,yo1与yo2分别为两个目标输出,ŷo1与ŷo2分别为神经网络输出,ŷh1与ŷh2分别为两个隐藏层输出,w1~w8分别为要调整的权重,x1与x2分别为两个输入。
我们的目标通过通过输入调整参数w1~w8使得输出接近目标输出。根据我们在4.2节中发现核心实际上是得到每次迭代后的Δwi 。
那么根据4.2节的内容,从隐藏层到输出的参数Δw5~Δw8,采用链式求导可以计算为
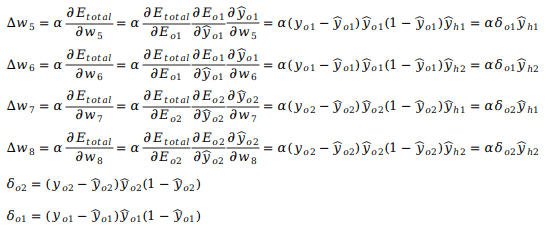
δo实际上表示输出层误差项。
到输出的权重更新完成后,接下来更新隐藏层权重,
隐含层的权重更新,需要知道各隐藏层节点的误差对最终输出的影响。每层的输出是由两层间的权重决定的,两层之间产生的误差,按权重缩放后在网络中向前传播。既然我们知道输出误差,便可以用权重来反向传播到隐藏层的权重Δw1~Δw4。
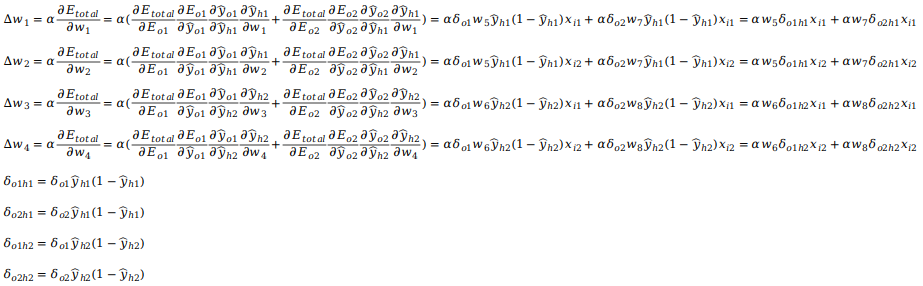
δoh实际上表示输出层误差项。
讲反向传播采用类似随机梯度下降的方式,则反向传播的pipeline可以写成:
- 随机设置初始权重
- 对训练数据当中的每一个样本,
- 让它正向传播通过网络,计算输出:ŷ ;
- 计算输出节点的误差项:δo ;
- 误差传播到隐藏层的误差项:δoh ;
- 更新权重步长:
- 输出层节点权重更新:Δwo = Δwo + δŷh ;
- 隐藏层节点权重更新:Δwh = Δwh + δŷh ;
- 第一层节点权重更新:Δwi = Δwi + δxi ;
- 更新权重:
- wi+1 = wi + αΔw
- 重复这个过程,直至迭代步数结束 。
※※从这里可以看出,误差项是从输出层权重更新,逐层传播到隐藏层权重更新。
※※从公式同样可以看出,如果函数中的每个值都经过前向传播计算得到,实际上反向传播每个值的计算是相互独立的,这就为并行计算(GPU)提供了条件,这也就是深度学习为什么可以采用GPU计算的原因。
※※我们采用的误差项计算是通过sigmoid求导得到的,f'(h) = f(h)(1 - f(h)),从导数的公式可以看出,sigmoid的导数最大值为0.25,在求导过程中,数值会越来越小,对产生梯度消失。所以在深度学习采用如reLu等激活函数。
参考资料
[2] https://www.cnblogs.com/hgl0417/p/5902042.html
[3] https://www.cnblogs.com/hgl0417/p/6670913.html
[4] https://www.cnblogs.com/hgl0417/p/5893930.html
[5] https://blog.csdn.net/weixin_38347387/article/details/82936585