B
有n个盒子需要你捡,第i个盒子的坐标为 (Xi , Yi)。你从(0,0)出发,每次只能选择向上或者向右移动,问能否将n个盒子都捡完,若可以捡完,则输出字典序最小的一条路线
简单模拟
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2005;
int b,c,n,m,T;
int L[1001],R[1001];
struct node{
int x,y;
}a[N];
string s;
bool cmp(node p,node pp)
{
if(p.x==pp.x) return p.y<pp.y;
else return p.x<pp.x;
}
int main()
{
scanf("%d",&T);
while(T--){
int vis=0;
s.clear();
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d",&a[i].x,&a[i].y);
}
// puts("bug");
sort(a+1,a+1+n,cmp);
int lastx=0,lasty=0;
for(int i=2;i<=n;i++){
if(a[i].x!=a[i-1].x&&a[i].y<a[i-1].y) {vis=1;break;}
}
if(vis) {puts("NO");continue;}
puts("YES");
for(int i=1;i<=n;i++) {
for(int j=lastx;j<a[i].x;j++) s.push_back('R');
for(int j=lasty;j<a[i].y;j++) s.push_back('U');
lastx=a[i].x,lasty=a[i].y;
}
cout<<s<<endl;
}
}
C
给你一个 n ,要求三个整数 a ,b ,c 使得 a * b * c = n 并且 a、b、c >= 2
分析:
先枚举 n 的因子,再判断因子是否可以再分解即可
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
vector<int> a;
typedef long long ll;
int main()
{
int n,t;
scanf("%d",&t);
while(t--){
int cnt=0;
a.clear();
scanf("%d",&n);
for(ll i=2;i*i<=n;i++){
if(n%i==0){
a.push_back(i);
cnt++;
n/=i;
}
if(cnt==3) break;
}
if(n!=1){
if(a.size()==3) a.back()*=n;
else a.push_back(n);
}
if(a.size()<3) cout<<"NO"<<endl;
else{
if(a[0]==a[1]||a[1]==a[2]||a[0]==a[2]) cout<<"NO"<<endl;
else cout<<"YES"<<endl,cout<<a[0]<<" "<<a[1]<<" "<<a[2]<<endl;
}
}
return 0;
}
D
给你 q 个询问和 一个 x , 每次询问输入一个数 n ,你可以把它与当前数组进行减任意次 x 或 加任意次 x,然后添入数组,问每次询问结束时数组里最小的没出现的非负整数是多少;
解法:
观察数据再手搓画一下我们发现,m>=x是“没有作用”的。解释就是每个元素你不断加多次x都无所谓,因为他的题意是其中的最小值,
我们可以将已给区间看成无数个【0,x-1】;
|——————|—|——————|—|——————————————|
0 x-1 0 x-1 0 ........
因为每个元素加x或减掉x,实际上就在这些间隔为x的新元素中寻找最小,例如m=5,x=3,可以推出2,5,8,11....,此时a=2;
此时最小是0,其中再来个m=0,此时a=0,2;最小是1,再来个m=1,a=0,1,2,最小是3,再来个m=10,可有1,4,7,10,13....,你会发现我们只需要他造出来的第一个区间里没有的例如10传出来的1,4区间有了,但是7没有,那就把7加进去,所以我们发现一个元素只给区间贡献一个规律的位置,例如10闯出来的,其实mod x后就是1,所以我们将坐标看成上面的,每次元素我们都mod x,进行记录次数,表示区间有多少个该位置被占了,然后在遍历一遍来mex
cnt [i] 表示此次询问时,若干个区间一共有cnt[i] 个 i 可以填到若干个区间中的 i 位置上(为了满足题目要求,我们从第一个区间的第i个位置开始填,然后再填第二个区间第i个位置)
然后我们从第一个区间开始检查。若到当前位置时cnt[i] != 0,则我们让cnt[i] --(表示我们拿一个i填在这个位置上),同时往下一个位置跳,直到遇到一个没有数可填的位置——cnt[pos] = 0
#include<bits/stdc++.h>
using namespace std;
map<int , int>cnt;
int main()
{
int q , x , ans = 0;
cin >> q >> x;
while(q --)
{
int n;
cin >> n;
cnt[n % x] ++;
while(cnt[ans % x])
cnt[ans % x] -- , ans ++;
cout << ans << '
';
}
return 0;
}
E
题意:
给你一个 n * m 的矩阵,你执行两种操作:
① 把矩阵中任意一个元素改为任意一个数
② 把矩阵中任意一列整体往上挪一个单元格,如下图矩阵我们对第一列向上挪了一个单元格
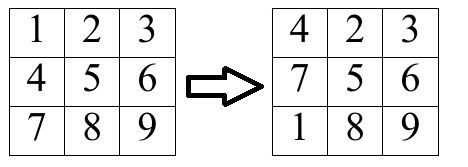
现要求用最少的操作次数使矩阵内每一个元素 a[i][j] = (i - 1) * m + j
分析:
因为题目只能对一列或者一个元素进行操作,所以我们逐列进行维护。
对第i行第j列的元素a[i][j] 我们假设它将成为这列的起点(第一个元素) 那么最坏的操作次数cost[i]为 i + N (把它移动到第1位需要i次 如果元素全都很奇葩需要更改N次)
对于每一列的操作,我们先初始化cost[i] = i + N , 然后如果a[i][j]可以作为第h行的答案的答案,那么cost[h] --(把a[h][j]行设为起点的最坏操作- 1)
最后遍历cost[1] ~ cost[n] 挑选最小的cost加到ans里即可
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int main()
{
int n , m ;
cin >> n >> m;
vector<vector<int>>a(n , vector<int>(m));
for(int i = 0 ; i < n ; i ++) for(int j = 0 ; j < m ; j ++)
{
cin >> a[i][j];
a[i][j] --;
}
int ans = 0;
for(int j = 0 ; j < m ; j ++)
{
vector<int>cost(n);
for(int i = 0 ; i < n ; i ++) cost[i] = i + n;
for(int i = 0 ; i < n ; i ++)
{
if(a[i][j] % m == j && a[i][j] < n * m)
{
int h = i - a[i][j] / m;
if(h < 0) h += n;
cost[h] --;
}
}
ans += *min_element(cost.begin() , cost.end());
}
cout << ans << '
';
return 0;
}
F
给你一棵树,要求你找出任意三点 A,B,C,使得 A~B,B~C,A~C 之间的边最多(边并集最大)
分析:
可证明一组最优解中一定有两个点是直径的两端点,那么题目就转换成求树直径端点及与两端点边并集最大的点,于是就很简单了
我们先一次bfs求出树直径DIS即其一端点A,再对端点A进行bfs求出另一端点B及每个点到端点A的距离dis1[i],最后再bfs端点B求出每个点到B的距离dis2[i]
最后遍历每个点,取边并集最大的即可(边并集= dis1[i]+dis2[i]−DIS2+DISdis1[i]+dis2[i]−DIS2+DIS)
现在给出证明:
假设某个答案取连接点x。x最远的树到达的点是s,根据树的直径算法,s是树的某个直径a的端点。假设x的最远和第二远的点组成的链是b,b就会和a有一段公共部分。我们取a和b相交部分距离s最远的那个点y。那么取这个链上点y的答案一定比x更优
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+10;
int n,m,T,tot,d[maxn],h[maxn*2],vis[maxn],dis1[maxn],dis2[maxn];
int DIS;
struct node
{
int w,nxt,to;
}edg[maxn*2];
void add(int u,int v,int w)
{
edg[tot].nxt=h[u];
edg[tot].w=w;
edg[tot].to=v;
h[u]=tot++;
}
int dfs(int x)
{
int u;
memset(d,0,sizeof(d));
memset(vis,0,sizeof(vis));
queue<int>q;
q.push(x);
vis[x]=1;
while(!q.empty()){
u=q.front();
q.pop();
for(int i=h[u];~i;i=edg[i].nxt){
int to=edg[i].to;
if(vis[to]) continue;
d[to]=d[u]+edg[i].w;
vis[to]=1;
q.push(to);
DIS=max(DIS,d[to]);
}
}
return u;
}
int main()
{
memset(h,-1,sizeof(h));
int a,b;
cin>>n;
int ans=0;
for(int i=1;i<n;i++){
cin>>a>>b;
add(a,b,1);
add(b,a,1);
}
int one,two,three;
one=dfs(1);
two=dfs(one);
for(int i=1;i<=n;i++) dis1[i]=d[i];
dfs(two);
for(int i=1;i<=n;i++) dis2[i]=d[i];
for(int i=1;i<=n;i++){
int res=(dis1[i]+dis2[i]-DIS)/2+DIS;
if(ans<res&&i!=one&&i!=two){
three=i;
ans=res;
}
}
cout<<ans<<'
'<<one<<" "<<two<<" "<<three<<endl;
}