时光飞逝,岁月如梭。在上一篇文章中,我们已经粗略地讨论了车辆的驱动原理,以及在直线行驶下的受力分析等,并且在文中我们给出了一些公式和相应的推导过程,相信你已对此有所了解。那么接下来,我们将在此基础上,更进一步的来谈一谈车辆的转向过程。
注意,本文某些部分的说明基于了上一篇的一些结论,所以如果你还没有看过上一篇文章的话,那么强烈建议你先去扫一眼再来。
此外,为了更好的说明一些基础的知识,本文基于了如下几个前提:
1. 本文不考虑转向时两前轮之间的角度差异(即我假设了两前轮在任何时候始终保持平行)。实际上,真实的车辆在转向时,两个前轮一般会在角度上存在一定偏差,但我想对于大多数游戏实现来说,应该不会考虑这种偏差。但如果你对此感兴趣的话,可以搜一搜相关的关键词:Ackermann steering geometry。
2. 本文仅针对后轮驱动的车辆进行讨论。相较于四驱或前驱来说,后驱是一种相对比较简单的情况,因为牵引力仅由后轮产生,且后轮不存在转向,因此这种情况下牵引力的方向将始终指向车头(或车尾)方向,这也意味着,牵引力将仅仅用于计算车辆沿车头/车位方向的加速度, 而不会存在一个侧向的分量来影响转向的过程。但如果你要考虑前驱或者四驱的话,那么由于此时前轮上产生了牵引力,并且前轮存在转向的情况,因此你就要多考虑一点前轮牵引力的角度问题了(这也不太难,大致上多了一个力的分解过程:分解到两个方向上进行单独考虑)。
3. 我们还是不考虑重心转移的问题,至于原因后文会提到。
Ok,预备事项表完,我们开扯。
首先我们先上关键的概念:轮胎与地面之间的“侧向力”(有些地方叫横向力,侧力,侧滑力等等,我也搞不清楚中文哪个更准确,英文叫lateral force或者cornering force,本文后面的部分将用“lateralForce”表示)。这便是在转向过程中起到最关键作用的一个力。它具体是指,当轮胎的旋转方向(滚动方向,或者说车轮的朝向)与实际的速度方向不一致的时候,所产生的一个指向轮胎侧面(正侧面,垂直于旋转的方向)的一个作用力。请参看下图:
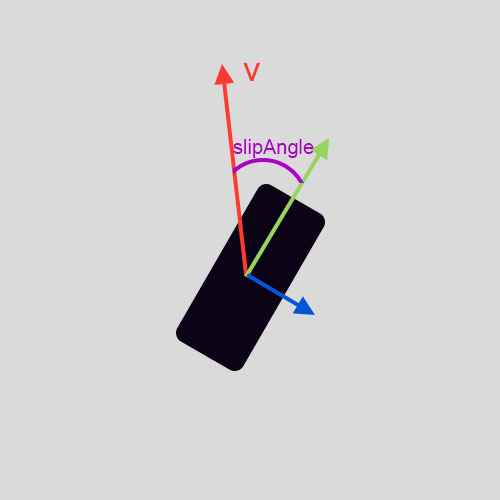
如该图所示,此刻一个车轮正在地面上滚动(俯视)。它的朝向如图上绿色箭头所示,而实际的速度方向如红色箭头v所示,并且车轮朝向与速度方向之间存在夹角为slipAngle(侧滑角),因此,图中的蓝色箭头代表的便是此刻轮胎与地面之间的侧向力,lateralForce(如果你把此图看成是一辆车的前轮的话,那么此刻的lateralForce导致了该车向右的转动)。
如果要深究lateralForce的成因的话,我看到过这样一种解释是说,当轮胎转向的时候,其与地面接触的部分并不会立即响应这种转向,因此在一个较短的时间内,该部分实际上产生了一个形变,而后为了恢复这种形变,从而引起了lateralForce(有点像弹力,神吧)。
不管怎样,既然已经明确了概念,那接下来我们就来看看这个力的计算。
首先,lateralForce与轮胎载重和slipAngle有关,并且在载重一定的情况下,lateralForce与slipAngle存在如下关系:

没错,跟上次发动机输出扭矩与RPM的关系图类似,这又是一份由轮胎厂家出具的图表,也是根据实验结果得到的。注意,我画的比较草率,有一点未标注,它一般是指在轮胎载重为5KN(即负载质量为500kg)的情况下,lateralForce与slipAngle的关系。从图上我们可以看出,当slipAngle大概在-5到5度之间时,lateralForce与slipAngle几乎成正比;当slipAngle超出这个范围的时候,lateralForce(的绝对值)稍有降低。因此,看到这种情况,很显然我们又要开始无耻地化简了:

由图可知,我们的策略显而易见:当slipAngle在-5与5之间时,我们认为lateralForce与slipAngle严格成正比关系;当slipAngle超出这个范围时,我们认为lateralForce始终取最大(或最小)值。 当然,关于lateralForce与slipAngle的关系,如果你觉得我的近似策略太过草率的话,还有一种更精致的办法也许适合你,请搜索:Pacejka Magic Formula。但如果你欣赏我这种简化方式的话,那我们便可以愉快地玩耍,并得到关于lateralForce的公式:
[公式1] lateralForce = fn * wheelLoad,
且:
fn = slipAngle * C, -fnMax <= fn <= fnMax
[公式1]的意思是说,先求一个“单位载重下的lateralForce”,即fn,它等于slipAngle乘以一个常数C(正比关系),并且我们限制:-fnMax <= fn <= fnMax,即一旦fn超出范围始终取端值;之后再用得到的fn乘以实际的轮胎载重wheelLoad,最终得到实际的lateralForce。
那么[公式1]中还有两个未知量,wheelLoad与slipAngle。我们首先来看wheelLoad,轮胎载重。这其实是在上一篇中提到过的一个名词,只是当时没有给出具体的计算方式。请看下图:

假设图中CG表示整车的重心位置,线段b表示前轮轴到重心的水平距离,线段c表示后轮轴到重心的水平距离,那么我们很容易知道,前后轮的载重与b和c长度成反比。所以,如果我们继续假设整车质量为m, 重力加速度为g的话,可得:
前轮载重(两前轮载重之和)等于:
[公式2] wheelLoadFront = m * g * c / (b + c)
后轮载重(两后轮载重之和)等于:
[公式3] wheelLoadRear = m * g * b / (b + c)
其中b+c即是所谓的轴距,wheelbase。一般的,如果你想更简单一些的话,你可以更进一步假设你的车辆重心位置就在轴距的中点,那么此时你理想地认为:wheelLoadFront = wheelLoadRear = m * g * 0.5。
至于slipAngle,在此我们先挂一个问号,稍后我们再回来讲解它的计算方法。
那接下来,我们便带入lateralForce,并结合上一篇文章所讲的知识,以及从车轮受力的角度出发,重新绘制我们的受力分析图:

如上图所示,有几个需要解释的地方:
1. 为何要把所有的着力点分别画在两条轮轴的中点,而不是画在每个车轮与地面的接触点上呢?的确,如果以实际情况出发,确实应该画在各个车轮与地面的接触点上。但为了简化过程,我们这里基于了两个假设,在文章开头已提到过,一是我们认为两个前轮(或两个后轮)在任何时候始终保持平行;另一个是我们不考虑重心转移的情况,即相应的左、右二轮在任何时候我们都认为是承受了相等的载重。在这两个假设的基础上,我们很容易想到,无论前后,相应的左、右二轮的受力分析是完全相同的。所以为了简单期间,我们不妨把两个前轮(或两个后轮)看成是一个整体,即当我们说前轮受力的时候,意思是指左右两前轮的受力之和;当说到后轮受力的时候,意思是指左右两后轮的受力之和。
2. 图中红色的几个箭头代表的全是在上一篇中提到的几个力,牵引力fraction,空气阻力drag以及滚动摩擦rollingResistance。它们本质上与前文提及的并无差别,此处仅仅是把它们分摊到了前、后轮上进行单独的考虑。具体包括:(一)由于我们仅考虑后轮驱动,因此fraction仅仅产生于后轮,并且永远指向车头或车尾方向;(二)为了表示起来方便,我们把drag也标在了后轮上,并且它的方向始终与速度方向相反(图示绿色箭头为速度方向);(三)由于转向期间前轮与后轮的角度不同,因此它们的滚动摩擦力方向也不同,这里用Front与Rear后缀以示区分。
为了更便于计算,我们不妨以车辆自身的坐标系为准,以车头的指向为long方向,以右侧面为lat方向,然后将上图所有的力都逐个分解到这两个方向上来,之后我们便得到了分解之后的图示:

虽然此图并不清晰,各个箭头并未进行文字标注,但事实上这也并不重要,你只需要知道这些箭头都是由上上图所标示的那些力,沿着long和lat方向分解而来。且此图的目的仅仅是为了方便你看出一个最终的结论,那便是:分解后所得到的所有沿long方向的力,它们形成的合力最终影响了车辆在long方向上的加速度;而所有沿lat方向的力嘛… 作用有两个:
一是和long方向的合力一样,lat方向的合力也最终形成了车辆在lat方向上的加速度(侧滑);
另一个作用是,也许你已经看出来了,它造成了车身绕其重心进行转动。
这便是整个转向过程的实质。
如果你很难想象这种转动的话,想象一根筷子嘛。。。是吧。

根据力矩公式,假设前轮上所受的沿lat方向合力为netForceLatFront,那么你可以计算它所形成的作用于车身旋转的力矩:
[公式4]torqueFront = netForceLatFront * b
同理,后轮上的力矩为:
[公式5]torqueRear = -netForceLatRear * c
(注意[公式5]的符号)。
那么,作用在整个车身上的合力矩就是torqueFront + torqueRear,即:
[公式6]torqueBody = netForceLatFront * b - netForceLatRear * c
之后可以再根据转动惯量公式,角加速度=合力矩/转动惯量inertia, 你可以得到车身转动的角加速度angularAcc公式为:
[公式7]angularAcc = (netForceLatFront * b - netForceLatRear * c)/ inertia
(关于转动惯量的定义,忘了的请自行搜索:moment of inertia。它跟物体的质量和形状有关,一般来说能查到。维基百科上列出了一些常用形状的转动惯量计算方法,总之对于特定的车型来说,转动惯量是已知量)
最后有了角加速度,你就可以计算车身旋转的角速度w,从而可以更进一步得到车身的角度(rotation)。
到此,整个转向的大致物理过程我们就介绍完了。有觉得豁然开朗了吗?
下面再回到上面留的一个问号,关于slipAngle的计算,这下就简单了。
根据定义,slipAngle是车轮朝向与车轮实际的速度方向(即车速方向)之间的夹角。既然如此,我们不妨将车速v也分解到long和lat两个方向上,如图vLong,vLat所示:

你可能一眼就能看出,既然slipAngle是车轮朝向与车轮速度方向之间的夹角,对于后轮来说,它的朝向就是指向long轴,速度方向就是车速的方向,那么它的slipAngle不就等于车速度方向与long轴形成的夹角吗?而这个夹角不就等于arctan(lat方向的速度分量 / long方向的速度分量的绝对值 )吗?因此,对于后轮:
slipAngleRear = arctan(lat方向的速度分量 / |long方向的速度分量 | )
其中long方向的速度分量即是图示的vLong,而值得注意的是lat方向的速度分量,可不仅仅只是图示的vLat。由于之前我们已经得出过结论,此时车身还在围绕重心以角速度w进行转动,并且根据角速度与速度之间的变换公式(速度等于角速度乘以旋转半径),我们能够得出另一个lat方向的速度,其大小等于w *c, 方向正好与vLat相反。因此,我们得到最终的后轮slipAngle公式为:
[公式8]slipAngleRear = arctan( (vLat - w*c) / |vLong| )
相应的,前轮与后轮基本同理,只不过由于前轮还存在一个转向角steerAngle(即前轮与long轴的夹角),这里稍微推导下可得,前轮slipAngle的公式为:
[公式9]slipAngleFront = arctan( (vLat + w*b) / |vLong| ) - sgn(vLong) * steerAngle
其中sgn(vLong)代表取vLong的符号(结果可为1,-1或0)。
到此,尽管整个过程可能让你有些眼花缭乱,但在不知不觉当中,截至[公式9],我们对整个物理情景的分析,就算是圆满结束了。
在本文的最后,结合之前的所有内容(包括上一篇文章),我最终整理了一份比较完善的有关车辆物理逻辑实现的基本算法流程,具体如下:
在你的update方法里:
1. 首先根据车辆相对于父级坐标系的速度v,结合车辆相对于父级的旋转角度rotation,计算出车辆相对于自身坐标系的速度分量vLong和vLat:
vLong = -sin(rotation) * v.y + cos(rotation) *v.x;
vLat = cos(rotation) * v.y + sin(rotation) * v.x;
2. 获取此时前轮的转向角度:steerAngle;
3. 根据vLong与vLat,计算风阻drag:
dragLong = -dragFactor * vLong *|vLong|;
dragLat = -dragFactor * vLat *|vLat|;
(这是算的drag在long和lat两个方向上的分量,下同。如果你够讲究,两式的dragFactor可能稍有不同,因为正面和侧面迎风面积不同)
4. 分别计算前后轮的滚动摩擦力:
前轮:
rollingResistanceFrontLong = -wheelLoadFront * cRR * cos(steerAngle);
rollingResistanceFrontLat = -wheelLoadFront * cRR * sin(steerAngle);
后轮:
rollingResistanceRearLong = -wheelLoadRear * cRR;
(后轮不存在lat方向的滚动摩擦力分量,即无rollingResistanceRearLat)
5. 根据油门throttle,发动机当前转速RPM,以及刹车力brakeForce和刹车情况brake,计算牵引力fraction:
fraction = f(RPM) * gearRatio * differentialRatio * efficiency / r * throttle + brake * brakeForce
(后轮驱动,fraction也不存在lat方向上的分量,之前讲过了)
6. 计算前轮slipAngle,并以此计算前轮lateralForce:
slipAngleFront = arctan( (vLat + w*b) / |vLong| ) - sgn(vLong) * steerAngle;
fnFront = slipAngleFront * C;
fnFront = clamp(-fnMax, fnMax);
lateralForceFrontLong = fnFront * wheelLoadFront * sin(steerAngle);
lateralForceFrontLat = fnFront * wheelLoadFront * cos(steerAngle);
7. 计算后轮slipAngle,并计算后轮lateralForce:
slipAngleRear = arctan( (vLat - w*c) / |vLong| ) ;
fnRear = slipAngleRear * C;
fnRear = clamp(-fnMax, fnMax);
lateralForceRear= fnRear * wheelLoadRear ;
(与前轮有所不同,lateralForceRear完全指向lat方向,因此不存在long方向的分量)
8. 综合上述得到的所有力,分别计算整车long和lat方向上受到的合力netForce(前后轮所有long方向与lat方向的合力分别相加):
netForceLong = rollingResistanceFrontLong + lateralForceFrontLong + rollingResistanceRearLong + dragLong + fraction;
netForceLat = rollingResistanceFrontLat + lateralForceFrontLat + dragLat + lateralForceRear;
9. 再根据合力和车辆质量,计算最终加速度,并根据刷新间隔时间delta,更新vLong,vLat:
aLong = netForceLong/ m;
aLat = netForceLat/ m;
vLong += aLong * delta;
vLat += aLat * delta;
10. 用更新后的vLong,vLat,参照第1步倒推,最终更新车辆相对于父级的速度v,并且更新坐标x,y。
...
x += v.x * delta;
y += v.y * delta;
11. 根据前后轮lat方向的受力算作用于车身上的合力矩(torqueBody = torqueFront + torqueWheel):
torqueBody = (lateralForceFrontLat + rollingResistanceFrontLat ) * b - lateralForceRear *c;
(注意这里貌似有点问题,应该还要考虑侧向的空气阻力…)
12. 根据合力矩,以及转动惯量inertia,算角加速度:
angularAcc = torqueBody / inertia;
13. 根据角加速度更新角速度w,并更新车身的旋转属性:
w += angularAcc * delta;
rotation += w * delta;
14. 更新rpm,如果是自动档的话检测是否该升降档。
完事。