【Swing作品】算24点软件

算24点是一种挺好的锻炼孩子算数能力的扑克牌游戏，它的游戏方式是把四张牌的牌面数值通过有限四则运算得到结果24，四张牌必须仅用一次。各地玩法还有点差别，有的只算1-10，其它抽出来；有的地方把整幅牌都算上，把其中J当作11,Q当作12，K当作13，小王当作15，大王当作18. 个人觉得后者不但省了理牌的功夫还更能锻炼人。

算24也是有窍门的，那就是逐步缩小范围，具体来说是看三个数运算能否和第四个数通过加减乘除得到24，继而看三个数操作能否得到24和第四个数的四则运算结果，继而看两个数的操作能否得到第三个数和上次结果的四则运算结果。具体比如有2，3，4，12四个数，看到12后想2，3，4是否能组合个2出来，然后想到2*3-4的方案，或者2*（4-3）的方案。

绝大多数四张牌的组合都容易算出来，有部分就要费点脑筋了，如5，5，5，1；3，7，3，7；12，12，12，10...，当然也有完全算不出来的，如5，7，8，11；1，1，6，11...从规律上讲，似乎5，7，11，13这样的素数参与越多越是难算. 如果您不确定四张牌能否算出24时，本软件正好能帮您解惑。

源码及执行包下载：https://files.cnblogs.com/files/heyang78/tweentyfour_bat_jar_src_210815pm.rar

码云地址：https://gitee.com/heyang78/twentyfour.git

使用前提：安装JDK1.8,若不会请参考 https://www.cnblogs.com/heyang78/p/7429783.html

使用方法：解压后双击run.bat执行

功能：提供四个正整数的计算24点的方案

界面截图：

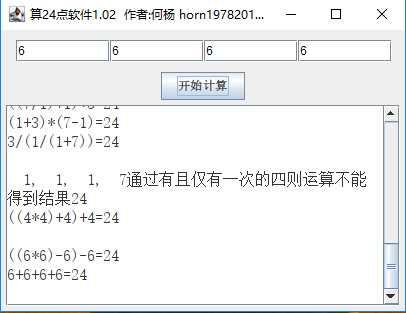
目前瑕疵：得到的方案里有重复,要解决两个算式是否同构算式的问题。

核心的五个类如下，相对于《Java常用算法手册》P444的方案，我觉得本作更清晰、五个类分工更明确，更何况此方案是完全自我胸中所出，并非随人脚后行！

Caculater类：

package com.hy.art;

import java.util.ArrayList;
import java.util.Collections;
import java.util.HashSet;
import java.util.List;
import java.util.Set;

/**
 * 用于计算24的对外类
 * @author 何杨 horn19782016@163.com
 * @version 创建时间：2021年8月14日 下午11:48:21
 */
public class Caculater {
    private double op1;
    private double op2;
    private double op3;
    private double op4;
    private final double Result=24;
    
    public Caculater(double op1,double op2,double op3,double op4) {
        this.op1=op1;
        this.op2=op2;
        this.op3=op3;
        this.op4=op4;
    }
    
    public Caculater(double[] arr) {
        this.op1=arr[0];
        this.op2=arr[1];
        this.op3=arr[2];
        this.op4=arr[3];
    }
    
    public List<String> findWays(){
        Set<String> ways=new HashSet<String>();
        
        C4 c4=new C4(this.op1,this.op2,this.op3,this.op4,Result);
        List<String> ls=c4.findWays();
        
        for(String line:ls) {
            line=line.replaceAll("((\d+)[.][0])", "$2");
            ways.add(line);
        }
        
        List<String> retval=new ArrayList<String>(); 
        retval.addAll(ways);
        Collections.sort(retval);
        
        return retval;
    }
    
    public static void main(String[] args) {
        Caculater c=new Caculater(12,6,4,1);
        List<String> ways=c.findWays();
        
        if(ways.size()>0) {
            for(String way:ways) {
                System.out.println(way);
            }
        }else {
            System.out.println("No way");
        }
        
    }
}

C4类：

package com.hy.art;

import java.util.ArrayList;
import java.util.List;

//======================================================
// C4类，用于判断三个数通过加减乘除运算能否得到某个结果
// C代表Caculate，4代表两个操作数
// op1:操作数1,op2:操作数2,op3:操作数3,op4:操作数4,result,结果
//======================================================
public class C4 {
    private double op1;
    private double op2;
    private double op3;
    private double op4;
    private double result;
    
    public C4(double op1,double op2,double op3,double op4,double result) {
        this.op1=op1;
        this.op2=op2;
        this.op3=op3;
        this.op4=op4;
        this.result=result;
    }
    
    public List<String> findWays(){
        List<String> ways=new ArrayList<String>();
        
        // 全排列数组，四个操作数共有24种排列方式
        double[][] permutationArr={  {this.op1,this.op2,this.op3,this.op4},
                                     {this.op1,this.op2,this.op4,this.op3},
                                     {this.op1,this.op3,this.op2,this.op4},
                                     {this.op1,this.op3,this.op4,this.op2},
                                     {this.op1,this.op4,this.op2,this.op3},
                                     {this.op1,this.op4,this.op3,this.op2},
                                     {this.op2,this.op1,this.op3,this.op4},
                                     {this.op2,this.op1,this.op4,this.op3},
                                     {this.op2,this.op3,this.op1,this.op4},
                                     {this.op2,this.op3,this.op4,this.op1},
                                     {this.op2,this.op4,this.op1,this.op3},
                                     {this.op2,this.op4,this.op3,this.op1},
                                     {this.op3,this.op1,this.op2,this.op4},
                                     {this.op3,this.op1,this.op4,this.op2},
                                     {this.op3,this.op2,this.op1,this.op4},
                                     {this.op3,this.op2,this.op4,this.op1},
                                     {this.op3,this.op4,this.op1,this.op2},
                                     {this.op3,this.op4,this.op2,this.op1},
                                     {this.op4,this.op1,this.op2,this.op3},
                                     {this.op4,this.op1,this.op3,this.op2},
                                     {this.op4,this.op2,this.op1,this.op3},
                                     {this.op4,this.op2,this.op3,this.op1},
                                     {this.op4,this.op3,this.op1,this.op2},
                                     {this.op4,this.op3,this.op2,this.op1},
                                   }; 
        
        for(int i=0;i<permutationArr.length;i++) {
            double[] innerArr=permutationArr[i];
            
            double oprand1=innerArr[0];
            double oprand2=innerArr[1];
            double oprand3=innerArr[2];
            double oprand4=innerArr[3];
            
            // [op1,op2,op3]-op4
            C3 c3=new C3(oprand1,oprand2,oprand3,this.result+oprand4);
            List<String> c3Ways=c3.findWays();
            for(String c3Way:c3Ways){
                ways.add('('+c3Way+")"+"-"+oprand4);
            }
 
            // [op1,op2,op3]/op4
            c3=new C3(oprand1,oprand2,oprand3,this.result*oprand4);
            c3Ways=c3.findWays();
            for(String c3Way:c3Ways){
                ways.add('('+c3Way+")"+"/"+oprand4);
            }
 
            // [op1,op2,op3]+op4
            c3=new C3(oprand1,oprand2,oprand3,this.result-oprand4);
            c3Ways=c3.findWays();
            for(String c3Way:c3Ways){
                ways.add('('+c3Way+")"+"+"+oprand4);
            }
 
            // op4-[op1,op2,op3]
            c3=new C3(oprand1,oprand2,oprand3,oprand4-this.result);
            c3Ways=c3.findWays();
            for(String c3Way:c3Ways){
                ways.add(oprand4+"-"+'('+c3Way+")");
            }
 
            // [op1,op2,op3]*op4
            c3=new C3(oprand1,oprand2,oprand3,this.result/oprand4);
            c3Ways=c3.findWays();
            for(String c3Way:c3Ways){
                ways.add('('+c3Way+")"+"*"+oprand4);
            }
 
            // op4/[op1,op2,op3]
            c3=new C3(oprand1,oprand2,oprand3,oprand4/this.result);
            c3Ways=c3.findWays();
            for(String c3Way:c3Ways){
                ways.add(oprand4+"/"+'('+c3Way+")");
            }
 
            // 以下为C4中特有的先成对组合再看运算结果
            // 1
            if(isEqual(oprand1*oprand2-oprand3*oprand4,result)){
                ways.add(oprand1+"*"+oprand2+"-"+oprand3+"*"+oprand4);
            }
 
            // 2
            if(isEqual(oprand1*oprand2+oprand3*oprand4,result)){
                ways.add(oprand1+"*"+oprand2+"+"+oprand3+"*"+oprand4);
            }
 
            // 3
            if(isEqual(oprand1/oprand2-oprand3/oprand4,result)){
                ways.add(oprand1+"/"+oprand2+"-"+oprand3+"/"+oprand4);
            }
 
            // 4
            if(isEqual(oprand1/oprand2+oprand3/oprand4,result)){
                ways.add(oprand1+"/"+oprand2+"+"+oprand3+"/"+oprand4);
            }
     
            // 5
            if(isEqual(oprand1*oprand2-oprand3/oprand4,result)){
                ways.add(oprand1+"*"+oprand2+"-"+oprand3+"/"+oprand4);
            }
 
            // 6
            if(isEqual(oprand1*oprand2+oprand3/oprand4,result)){
                ways.add(oprand1+"*"+oprand2+"+"+oprand3+"/"+oprand4);
            }
            
            // 7
            if(isEqual((oprand1+oprand2)*(oprand3-oprand4),result)){
                ways.add("("+oprand1+"+"+oprand2+")*("+oprand3+"-"+oprand4+")");
            }
            
            // 8
            if(isEqual((oprand1+oprand2)/(oprand3-oprand4),result)){
                ways.add("("+oprand1+"+"+oprand2+")/("+oprand3+"-"+oprand4+")");
            }
            
            // 9
            if(isEqual((oprand1-oprand2)*(oprand3-oprand4),result)){
                ways.add("("+oprand1+"-"+oprand2+")*("+oprand3+"-"+oprand4+")");
            }
            
            // 10
            if(isEqual((oprand1-oprand2)/(oprand3-oprand4),result)){
                ways.add("("+oprand1+"-"+oprand2+")/("+oprand3+"-"+oprand4+")");
            }
            
            // 11
            if(isEqual((oprand1+oprand2)*(oprand3+oprand4),result)){
                ways.add("("+oprand1+"+"+oprand2+")*("+oprand3+"+"+oprand4+")");
            }
            
            // 12
            if(isEqual((oprand1+oprand2)/(oprand3+oprand4),result)){
                ways.add("("+oprand1+"+"+oprand2+")/("+oprand3+"+"+oprand4+")");
            }
        }
        
        return ways;
    }
    
    // 判断两个double数是否相等
    private static boolean isEqual(double d1,double d2){
        return Math.abs(d1-d2)<0.0001;
    }
    
    public static void main(String[] args) {
        C4 c4=new C4(2,4,6,8,24);
        List<String> ls=c4.findWays();
        
        if(ls.size()>0) {
            for(String line:ls) {
                System.out.println(line);
            }
        }else {
            System.out.println("No way.");
        }
    }
}

C3类：

package com.hy.art;

import java.util.ArrayList;
import java.util.List;

//======================================================
// C3类，用于判断三个数通过加减乘除运算能否得到某个结果
// C代表Caculate，3代表三个操作数
// op1:操作数1,op2:操作数2,op3:操作数3,result,结果
//======================================================
public class C3 {
    private double op1;
    private double op2;
    private double op3;
    private double result;
    
    public C3(double op1,double op2,double op3,double result) {
        this.op1=op1;
        this.op2=op2;
        this.op3=op3;
        this.result=result;
    }
    
    public List<String> findWays(){
        List<String> ways=new ArrayList<String>();
        
        // 排列数组，三个操作数共有6种排列方式
        double[][] permutationArr= {
                            {this.op1,this.op2,this.op3},
                            {this.op1,this.op3,this.op2},
                            {this.op2,this.op1,this.op3},
                            {this.op2,this.op3,this.op1},
                            {this.op3,this.op2,this.op1},
                            {this.op3,this.op1,this.op2},
        };
        
        for(int i=0;i<permutationArr.length;i++) {
            double[] innerArr=permutationArr[i];
            
            double oprand1=innerArr[0];
            double oprand2=innerArr[1];
            double oprand3=innerArr[2];
            
            // [op1,op2]-op3
            C2 c2=new C2(oprand1,oprand2,this.result+oprand3);
            List<String> c2Ways=c2.findWays();
            for(String c2Way:c2Ways){
                ways.add('('+c2Way+")"+"-"+oprand3);
            }
            
            // [op1,op2]/op3
            c2=new C2(oprand1,oprand2,this.result*oprand3);
            c2Ways=c2.findWays();
            for(String c2Way:c2Ways){
                ways.add('('+c2Way+")"+"/"+oprand3);
            }
 
            // [op1,op2]+op3
            c2=new C2(oprand1,oprand2,this.result-oprand3);
            c2Ways=c2.findWays();
            for(String c2Way:c2Ways){
                ways.add('('+c2Way+")"+"+"+oprand3);
            }
 
            // op3-[op1,op2]
            c2=new C2(oprand1,oprand2,oprand3-this.result);
            c2Ways=c2.findWays();
            for(String c2Way:c2Ways){
                ways.add(oprand3+"-"+'('+c2Way+")");
            }
 
            // [op1,op2]*op3
            c2=new C2(oprand1,oprand2,this.result/oprand3);
            c2Ways=c2.findWays();
            for(String c2Way:c2Ways){
                ways.add('('+c2Way+")"+"*"+oprand3);
            }
 
            // op3/[op1,op2]
            c2=new C2(oprand1,oprand2,oprand3/this.result);
            c2Ways=c2.findWays();
            for(String c2Way:c2Ways){
                ways.add(oprand3+"/"+'('+c2Way+")");
            }
        }
        
        return ways;
    }
}

C2类：

package com.hy.art;

import java.util.ArrayList;
import java.util.List;

/**
 * 
// C2类，用于判断两个数通过加减乘除运算能否得到某个结果
// C代表Caculate，2代表两个操作数
// op1:操作数1,op2:操作数2,result,结果
 * @author 何杨 horn19782016@163.com
 * @version 创建时间：2021年8月14日 下午10:55:57
 */
public class C2 {
    private double op1;
    private double op2;
    private double result;
    
    public C2(double op1,double op2,double result) {
        this.op1=op1;
        this.op2=op2;
        this.result=result;
    }
    
    public List<String> findWays(){
        List<String> ways=new ArrayList<String>();
        
        // 加一种
        if(isEqual(result,(op1+op2))) {
            ways.add(op1+"+"+op2);
        }
        
        // 乘一种
        if(isEqual(result,(op1*op2))) {
            ways.add(op1+"*"+op2);
        }
        
        // 减两种
        if(isEqual(result,(op1-op2))) {
            ways.add(op1+"-"+op2);
        }
        
        if(isEqual(result,(op2-op1))) {
            ways.add(op2+"-"+op1);
        }
        
        // 除两种
        if(isEqual(result,(op1/op2))) {
            ways.add(op1+"/"+op2);
        }
        
        if(isEqual(result,(op2/op1))) {
            ways.add(op2+"/"+op1);
        }
        
        return ways;
    }
    
    // 判断两个double数是否相等
    private static boolean isEqual(double d1,double d2){
        return Math.abs(d1-d2)<0.0001;
    }
}

-END-