Javaday13(基础数据结构)

一、基础数据结构

　　数据元素相互之间的关系称为结构。

　　具备关联关系的非松散集合性结构主要有三种：

　　　　1.线性表：节点按逻辑关系依次排列形成一个“锁链”。

　　　　2.树：具有分支，层次特性，其形态有点像自然界中的树。

　　　　3.图：节点按逻辑关系相互缠绕，任何两个节点是一种物理连续的线性表。

　　数组其实就是一种典型的线性表，而且是一种物理连续的线性表，特点：

　　　　1.通过下标可以直接访问元素

　　　　2.数组中每一个元素的类型必须一致

　　　　3.数组的大小一旦确定就不能再次发生改变

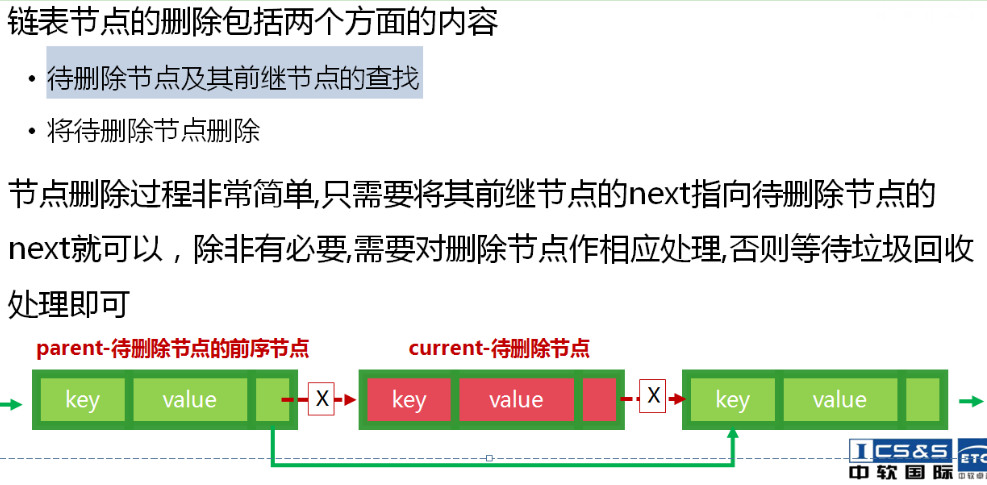
　　链表的出现解决了数组的一些问题：

　　　　1.插入，删除的效率过低

　　　　2.数组大小不可变，不能动态生成

　　数组和链表的区别：

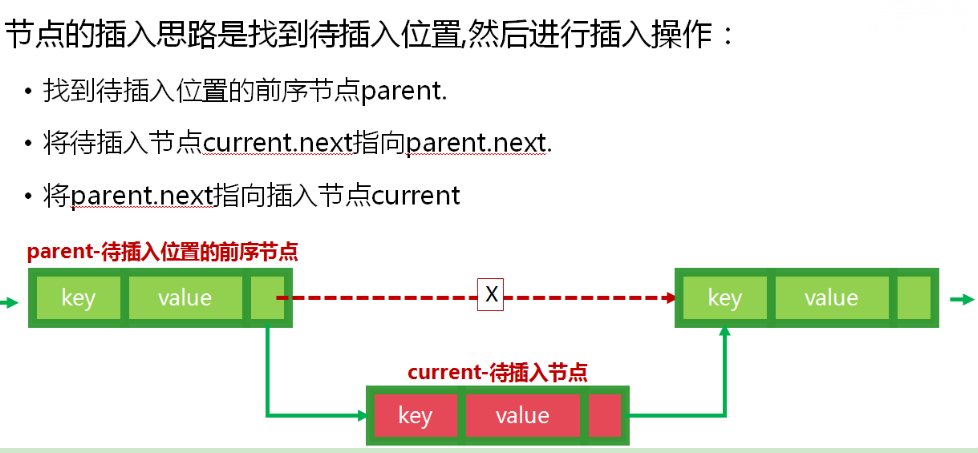
　　　　1.链表的插入和删除效率要比数组要高

　　　　2.链表可以动态增长或者减小

　　　　3.数组中的内容是在内存中连续存储的，所以在查询效率上来说数组更占优。

　　链表（模拟）：

　　　　

　　       

 　　　　

               

               

　　　  

　　　

　　　　

 　　　

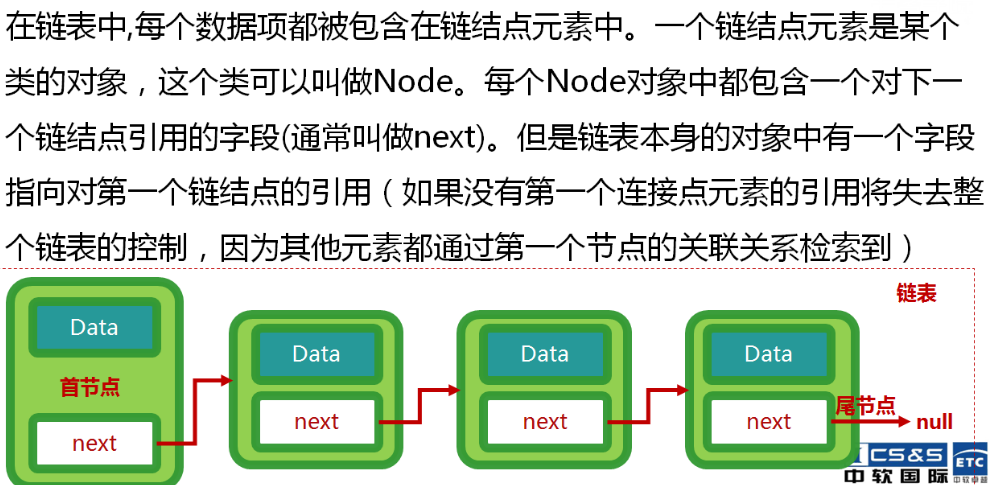
　　栈（模拟）：后进先出

　　    

 　　　　  

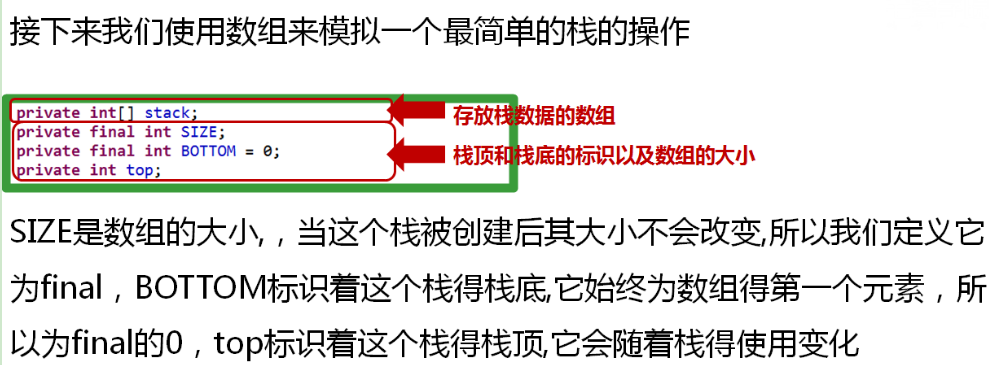
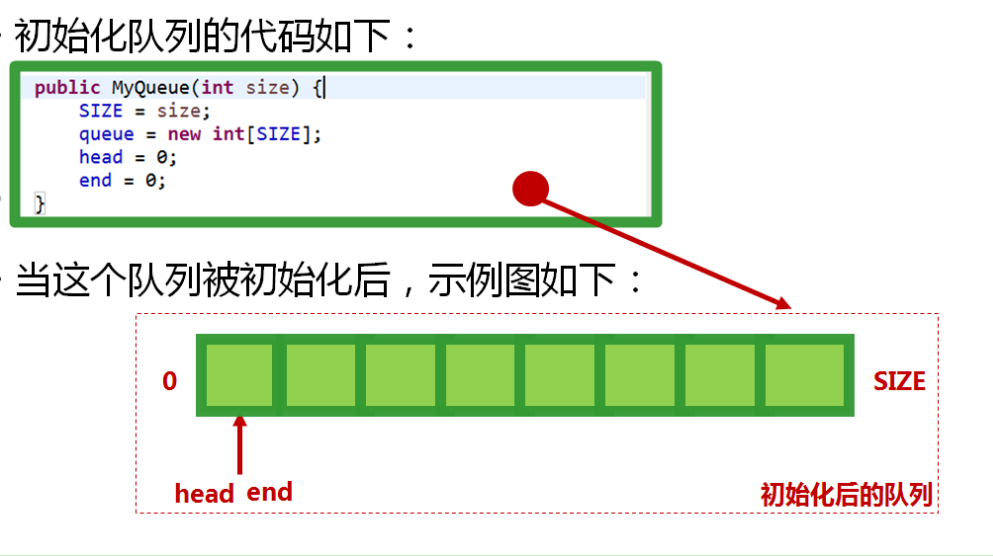
　　　　在初始化栈时：

　　　　1.存储空间需要初始化，如果是动态的仅仅需要得到其大小和初始空间的创建

　　　　2.栈底通常定义与于存储空间的一段，而且通常是默认值（0）

　　　　3.令栈顶指向栈底，top=bottom；

　　　此时：一个空的栈就被创建完成

　　　　

　　　　

　　　　

　　　　

　　　　  

 　　　　     

　　　　

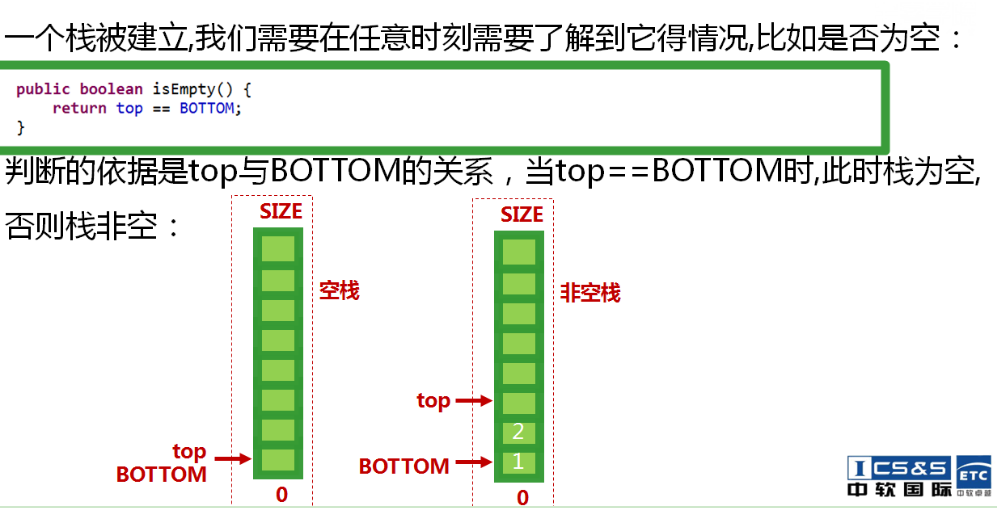
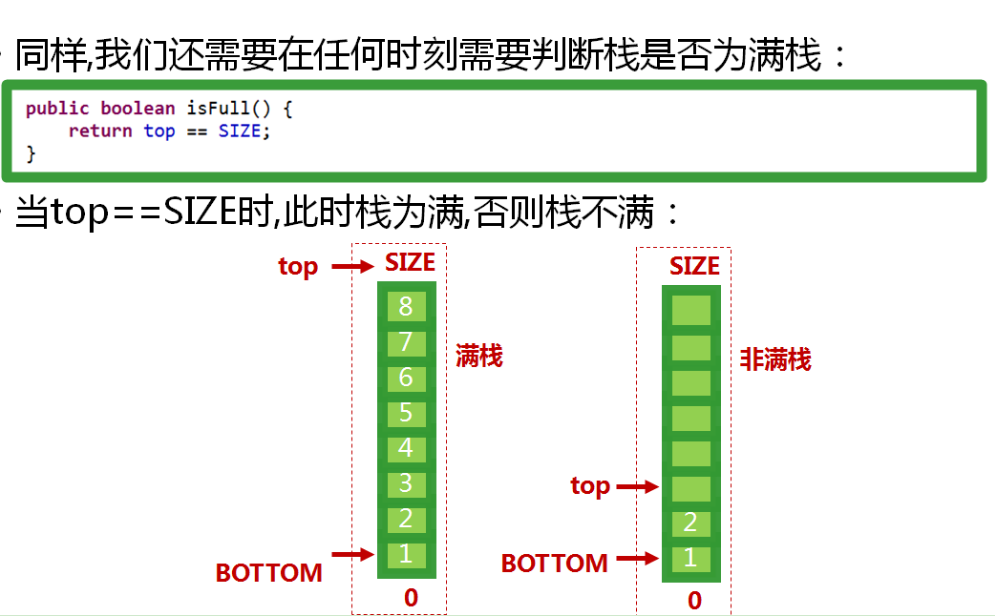
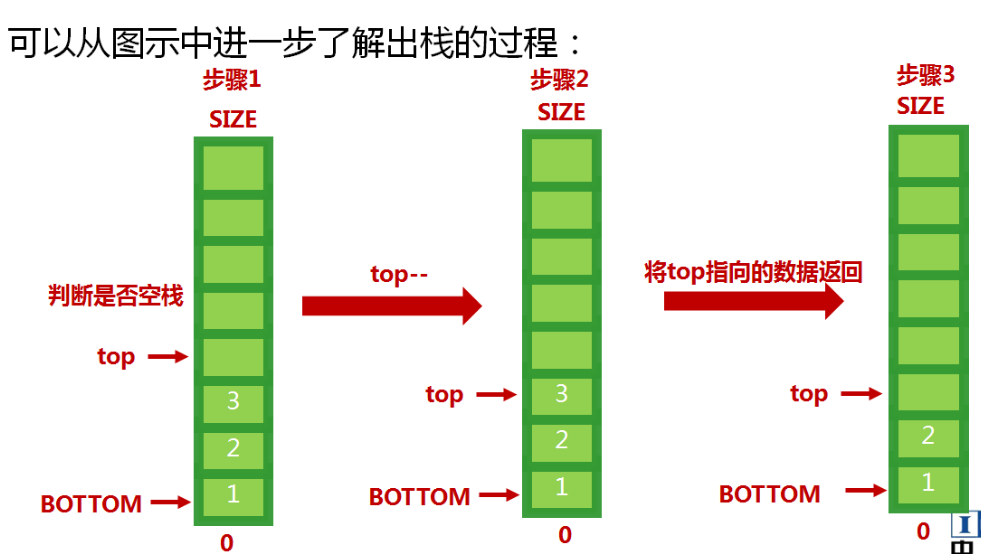
• • 　　在push()pop()方法中都使用了synchronized关键字
  • 　　这是为了使入栈与出栈操作原子化，就是说在入栈与出栈的操作过程中是不允许其它操作干扰的。有了同步的保障,栈的工作才不会出现异常

 　　队列（模拟）：queue

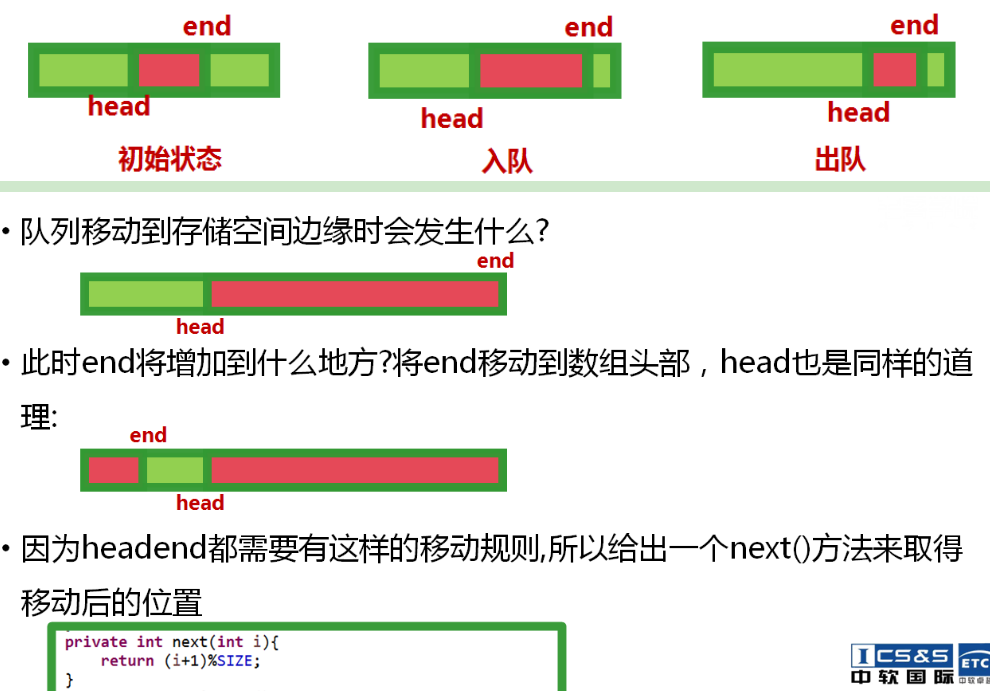
　　　　　　队列是“先入先出”的一种数据结构。

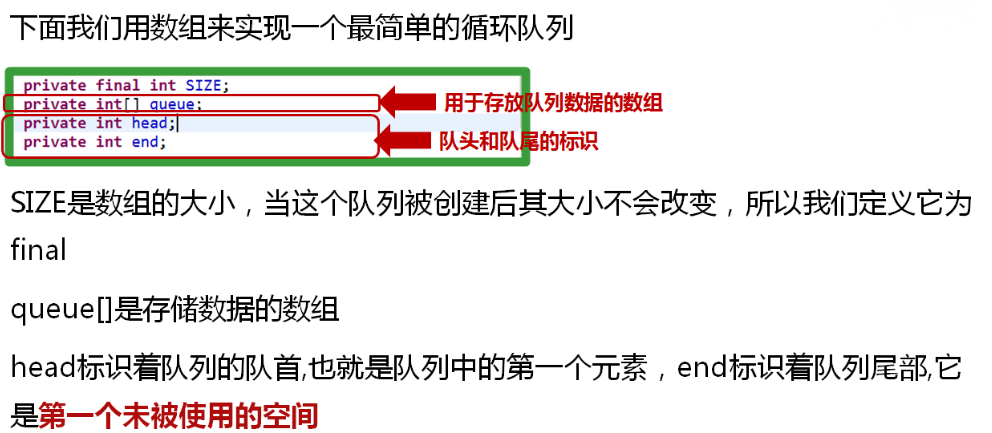
　　　　  同时也有两个标识符来表示队列的两端：对首（head）和对尾（end）。

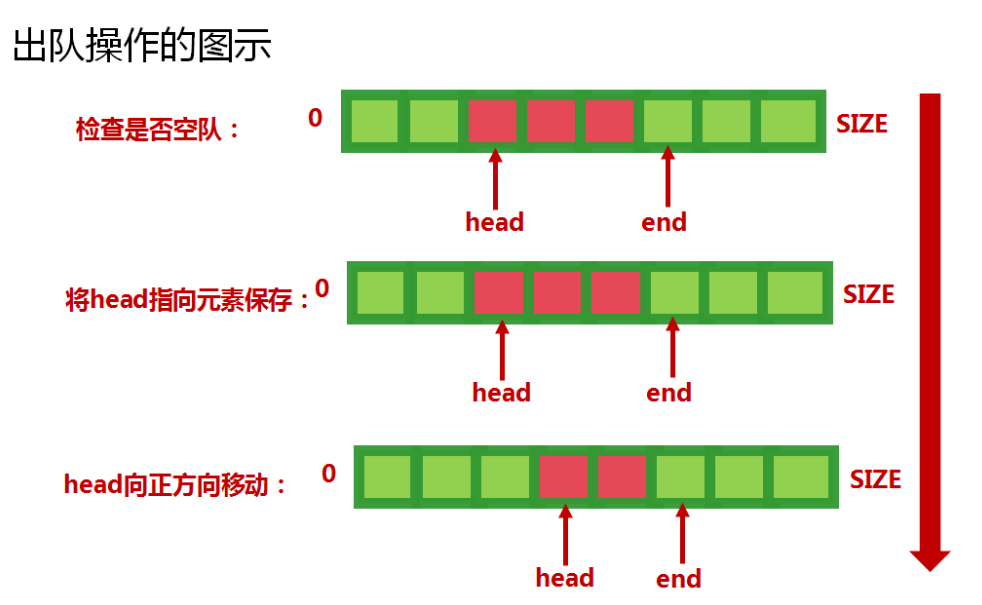
　　　　  队列同时也要提供两个方法：入队（offer）和出队（poll）

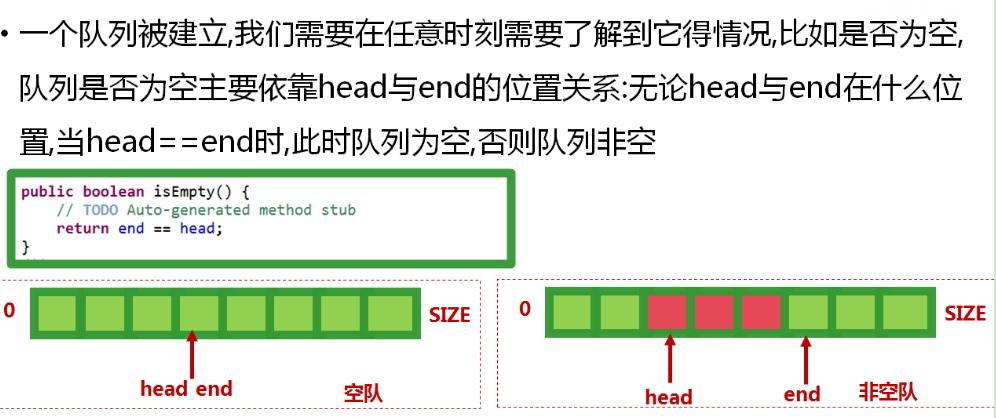
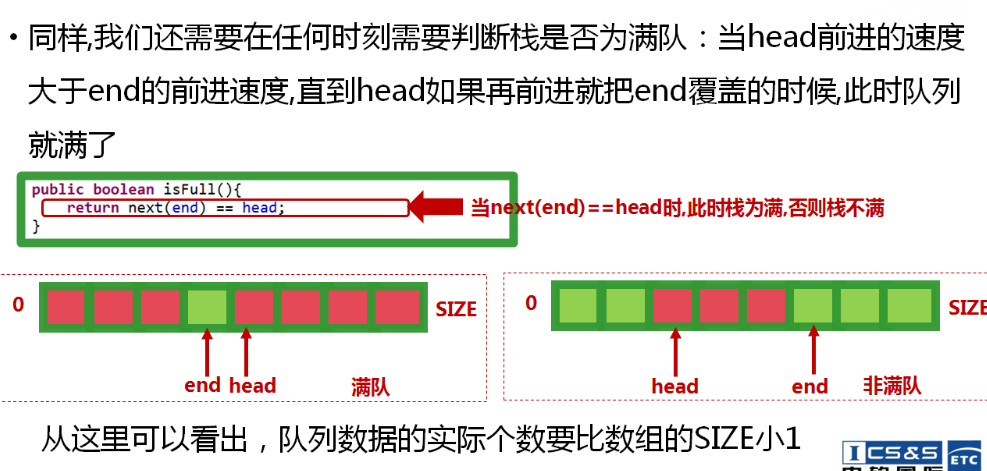
　　　　　　说明：head和end值初始化时一定为0，此时队列为空队列，offer入队操作后，head应该指向第一位入队的值，end指向入队的值，再次入队时，head继续指向第一个值，end指向新加入的值。

　　　　

 　　　　  

　　   

         

　　　　

 　　　　

 　　　　

           

 　　　　

 　　　Hash表也是一种复杂的数据结构：它主要作用于大量的数据中快速的定位检索到某个特定的数据，其存放的数据往往包含着两个部分：key和data，key作为存储和检索的索引，数据data存放实际的数据项。

　

• • 　　表中元素和关键字之间的关系由哈希函数确定，即hash（key）=位置 在构造这种特殊的“查找表”时，除了需要选择一个“好”(尽可能少产生冲突)的哈希函数之外,还需要找到一种“处理冲突”的方法 
    • 　　哈希函数是一个映象，即：将关键字的集合映射到某个地址集合上，它的设置很灵活，只要这个地址集合的大小不超出允许范围即可
    • 　　由于哈希函数是一个压缩映象，因此，在一般情况下，很容易产生“冲突”现象，即：key1≠key2，而hash(key1)=hash(key2)
    • 　　只能尽量减少冲突而不能完全避免冲突，这是因为通常关键字集合比较大，其元素包括所有可能的关键字，而地址集合的元素仅为哈希表中的地址值

 　　　　

• 实际造表时，采用何种构造哈希函数的方法取决于建表的关键字集合的情况(包括关键字的范围和形态)，以及哈希表长度（哈希地址范围），总的原则是使产生冲突的可能性降到尽可能地小

• “处理冲突”的实际含义是：为产生冲突的关键字寻找下一个哈希地址，包括开放定址法、再哈希法、链地址法等，链地址法被很多语言的Hash表默认实现所选择：

 

• 在Hash表中有一个非常重要的参数：装载因子
• 装载因子就是hash表中已经存储的关键字个数，与可以散列位置的比值，表征着hash表中的拥挤情况，一般而言，该值越大则越容易发生冲突
• Hash表的简单实现代码参考课堂案例 Hash表的装载因子 = 填入表中的元素个数 / Hash表的长度
  • 因为冲突的存在，其查找长度不可能达到O(1)
  • 哈希表的平均查找长度是装载因子a的函数，而不是n的函数
  • 用哈希表构造查找表时，可以选择一个适当的装载，使得平均查找长度限定在某个范围内

　　　　

　　

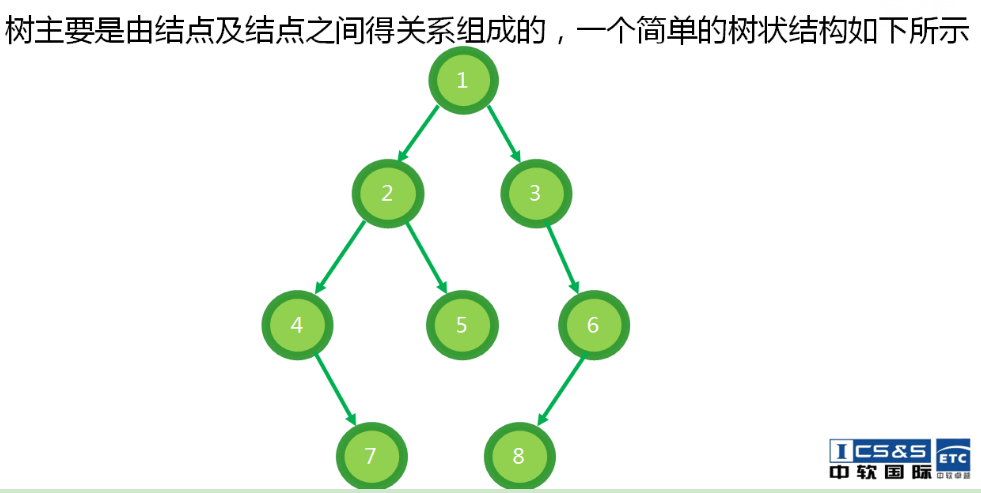
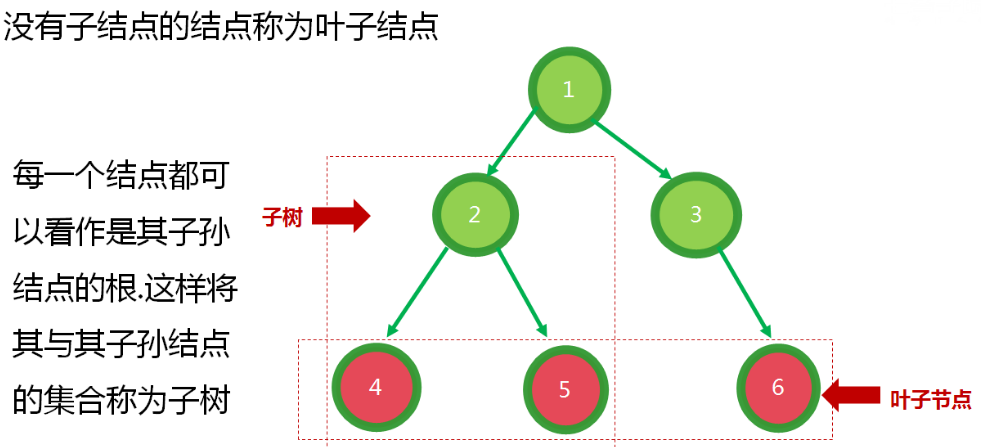
　　 树状图特点：

　　　　1.每个节点都有0或多个子节点

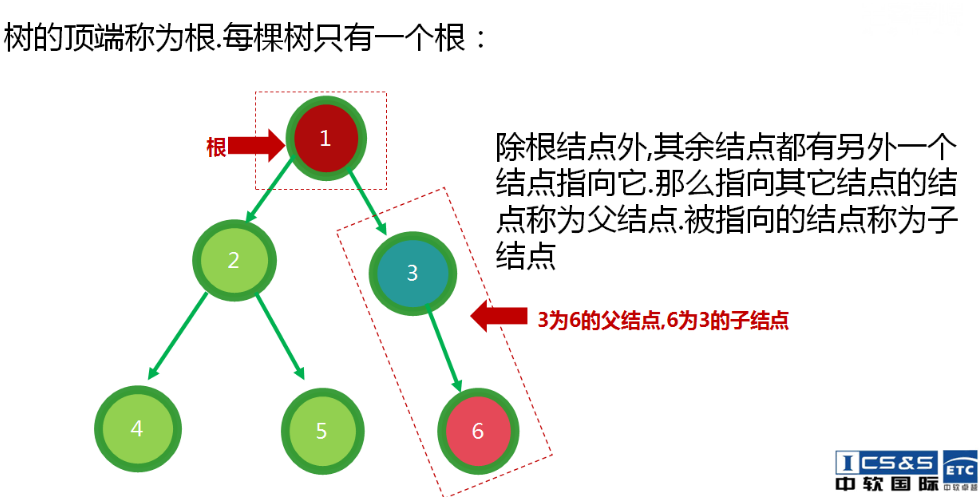
　　　　2.没有父节点的节点称为根节点

　　　　3.每一个非根节点都有一个父节点

　　　　4.除了根节点之外，每个子节点可以分为多个不想交的子树

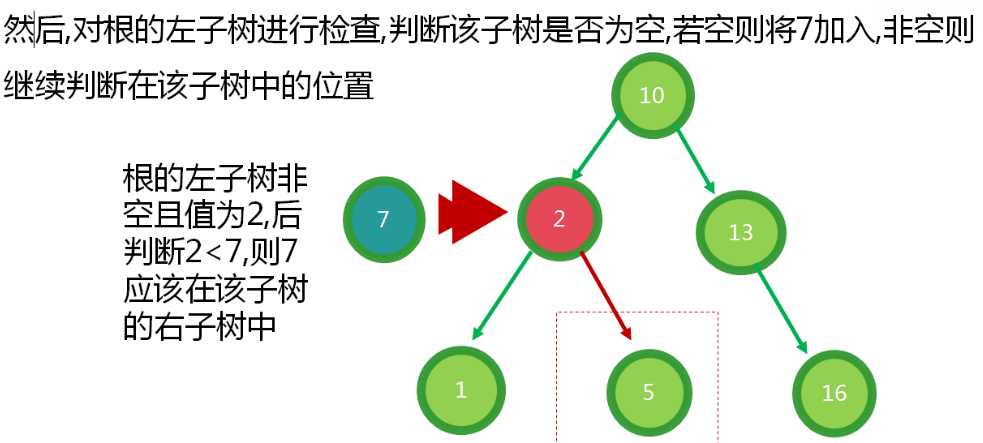
　　　　树状图之中使用频率最高的是二叉树，所谓的二叉树就是父节点上最多有两个子节点的树。

　　　　二叉树优点：较快的查询速度，插入和删除效率高。

　　    

　　　　

　　　　

 　　　　

 　　　　　　

　　　　     

　　　　   

 　　　　  

 　　　　

　　搜索二叉树的定义是根要大于左子树所有节点，小于右子树的所有节点，其子树依旧遵循这个规律