437 路径总和|||
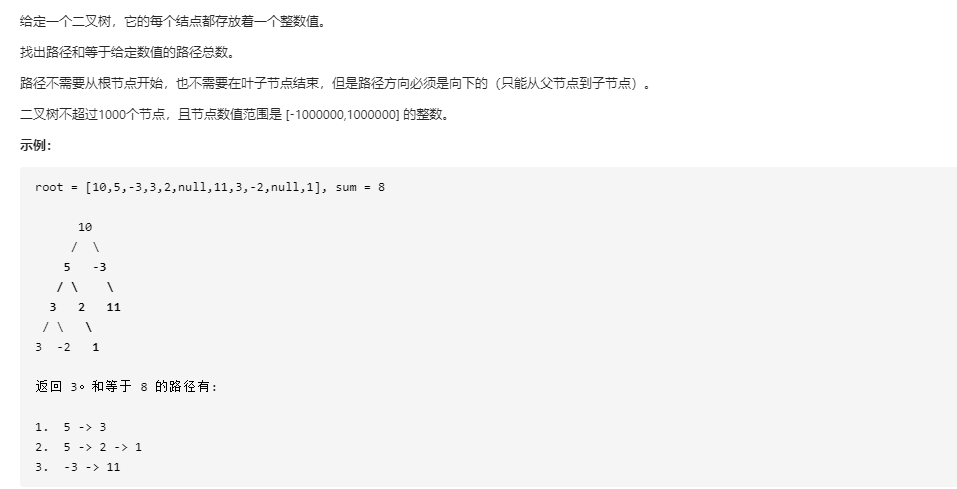
我的解法如下,但复杂度很高,想想也知道应该不是好的解法。。。
class Solution { int sum; LinkedList<Integer> list; int result; public int pathSum(TreeNode root, int sum) { if (root == null)return 0; this.sum = sum; list = new LinkedList<>(); result = 0; find(root); return result; } public void find(TreeNode root){ //计算 int val = root.val; if(val == sum){ result++; } for (Integer cr : list) { val+=cr; if (val == sum){ result++; } } list.addFirst(root.val); if (root.left != null){ find(root.left); } if (root.right != null){ find(root.right); } list.pollFirst(); } }
问题肯定是出在了重复计算上面,路径的和不断的被重复计算,所以需要想个办法记录下当前节点之前的阶梯计算结果,可以用一个hash表存下来. 涉及到前缀和的问题
class Solution { int sum; Map<Integer,Integer> map; int result; public int pathSum(TreeNode root, int sum) { if (root == null)return 0; this.sum = sum; map = new HashMap<>(); map.put(0,1); result = 0; find(root,0); return result; } public void find(TreeNode root,int s){ if (root == null)return; Integer count = map.getOrDefault(s+root.val-sum, 0); result+=count; map.put(s+root.val,map.getOrDefault(s+root.val,0)+1); find(root.left,s+root.val); find(root.right,s+root.val); map.put(s+root.val,map.get(s+root.val)-1); } }
449 序列化与反序列化二叉搜索树
写了个通用的,应该是不管二叉搜索树还是普通二叉树都能用
// Encodes a tree to a single string. public String serialize(TreeNode root) { if (root == null)return ""; List<TreeNode> list = new ArrayList<>(); list.add(root); StringBuilder sp = new StringBuilder(); boolean falg = true; while (falg){ falg = false; List<TreeNode> cs = new ArrayList<>(); for (TreeNode treeNode : list) { if (treeNode == null){ sp.append(" ").append(","); }else{ sp.append(treeNode.val).append(","); cs.add(treeNode.left); cs.add(treeNode.right); falg |= treeNode.left != null || treeNode.right != null; } } list = cs; } return sp.toString(); } // Decodes your encoded data to tree. public TreeNode deserialize(String data) { if (data.equals(""))return null; String[] arr = data.split(","); LinkedList <String> list = new LinkedList<>(); for (String s : arr) { list.add(s); } List<TreeNode> tps = new ArrayList<>(); TreeNode root = new TreeNode(Integer.valueOf(list.pollFirst())); tps.add(root) ; while (!list.isEmpty()){ List<TreeNode> cs = new ArrayList<>(); for (TreeNode tp : tps) { String lef = list.pollFirst(); tp.left = lef.equals(" ")?null:new TreeNode(Integer.valueOf(lef)); if (tp.left != null)cs.add(tp.left); String rig = list.pollFirst(); tp.right = rig.equals(" ")?null:new TreeNode(Integer.valueOf(rig)); if (tp.right != null)cs.add(tp.right); } tps = cs; } return root; }
450 删除二叉搜索树的节点
这题让我回想起了几年前写红黑树删除节点的恐惧。。。 ,还好这个应该只是删除,没有旋转操作,就是体力活
,还好这个应该只是删除,没有旋转操作,就是体力活
删除一般有两种方式,找到左边的最右子节点或者右边的最左子节点来替换这个被删除节点。
TreeNode parent; TreeNode rm; boolean leftSon, rightSon; public TreeNode deleteNode(TreeNode root, int key) { if(root == null)return null; if (root.val == key) { rm = root; } else { find(root, key); } if(rm == null){ return root; } if (parent == null) { //删除点为根节点 if (root.left == null || root.right == null) { return root.left != null ? root.left : root.right; } if (root.right != null) { TreeNode right = findRight(rm.right); rm.val = right.val; if (right.val == rm.right.val){ rm.right = right.right; } } return root; } else { if (rm.left == null || rm.right == null) { if (leftSon) { parent.left = rm.right != null ? rm.right : rm.left; } else { parent.right = rm.right != null ? rm.right : rm.left; } return root; } TreeNode right = findRight(rm.right); rm.val = right.val; if (right.val == rm.right.val){ rm.right = right.right; } return root; } } public TreeNode findRight(TreeNode node) { if (node == null) return null; if (node.left != null) { TreeNode left = findRight(node.left); if (node.left.val == left.val) { node.left = left.right; } return left; } return node; } public void find(TreeNode root, int key) { if(root == null)return; if (root.left != null && root.left.val == key) { parent = root; rm = root.left; leftSon = true; } else if (root.right != null && root.right.val == key) { parent = root; rm = root.right; rightSon = true; } else if (root.val > key) { find(root.left, key); } else { find(root.right, key); } }
508 出现次数最多的子树元素和

Map<Integer,Integer> map; int max; public int[] findFrequentTreeSum(TreeNode root) { map = new HashMap<>(); max = 0; List<Integer> data = new ArrayList<>(); Set<Integer> integers = map.keySet(); for (Integer integer : integers) { Integer c = map.get(integer); if (c.equals(max)){ data.add(integer); } } int[] result = new int[data.size()]; for (int i = 0; i < data.size(); i++) { result[i] = data.get(i); } return result; } public int find(TreeNode root){ if (root == null)return 0; int total = root.val; int left = find(root.left); int right = find(root.right); total+=left+right; Integer count = map.getOrDefault(total, 0)+1; map.put(total,count); max = Math.max(max,count); return total; }
513 找到树左下角的值

我的方法比较愚蠢了,复杂度很高
public int findBottomLeftValue(TreeNode root) { List<TreeNode> list = new ArrayList<>(); list.add(root); while (true){ List<TreeNode> c = new ArrayList<>(); for (TreeNode treeNode : list) { if (treeNode.left != null)c.add(treeNode.left); if (treeNode.right != null)c.add(treeNode.right); } if (c.isEmpty())return list.get(0).val; list = c; } }
其实可以想下,二叉树的不管哪种遍历方式左子树一定是比右子树先遍历到的,所以第一个到第N层的肯定就是最左边的值,所以根据这个定理可以用如下代码
class Solution { int max; int deep; public int findBottomLeftValue(TreeNode root) { max = 0; deep = 0; dfs(root,1); return max; } public void dfs(TreeNode root ,int dp){ if (root == null)return; if (dp > deep){ deep = dp; max = root.val; } dfs(root.left,dp+1); dfs(root.right,dp+1); } }
515 找到每行的最大值

这题和上题基本一模一样,所以也有上题的两种方式
1是容易理解但空间复杂度高的方法 BFS
public List<Integer> largestValues(TreeNode root) { List<TreeNode> list = new ArrayList<>(); list.add(root); List<Integer> result = new ArrayList<>(); if (root == null) return null; while (!list.isEmpty()){ List<TreeNode> c = new ArrayList<>(); int s = Integer.MIN_VALUE; for (TreeNode treeNode : list) { s = Math.max(s,treeNode.val); if (treeNode.left != null)c.add(treeNode.left); if (treeNode.right != null)c.add(treeNode.right); } list = c; } return result; }
2是效率高一些的方法 DFS
class Solution { Map<Integer,Integer> map; int max; public List<Integer> largestValues(TreeNode root) { List<Integer> result = new ArrayList<>(); if (root == null)return result; max = 0; map = new HashMap<>(); dfs(root,1); for (int i = 1; i <= max; i++) { result.add(map.get(i)); } return result; } public void dfs(TreeNode root,int level){ if (root == null)return; Integer val = map.getOrDefault(level, Integer.MIN_VALUE); if (root.val>=val){ map.put(level,root.val); } max = Math.max(max,level); dfs(root.left,level+1); dfs(root.right,level+1); } }
汗 原来自己写的BFS一直有问题,看了下官解,下面才是正规的BFS写法,空间复杂度O(n)
public List<Integer> largestValues(TreeNode root) { List<Integer> result = new ArrayList<>(); if (root == null)return result; LinkedList<TreeNode> stack = new LinkedList<>(); stack.addLast(root); while (!stack.isEmpty()){ int size = stack.size(); int s = Integer.MIN_VALUE; for (int i = 0; i < size; i++) { TreeNode treeNode = stack.pollLast(); if (treeNode.val>=s){ s = treeNode.val; } if (treeNode.left!=null)stack.addFirst(treeNode.left); if (treeNode.right!=null)stack.addFirst(treeNode.right); } result.add(s); } return result; }
538 二叉树转换为累加树
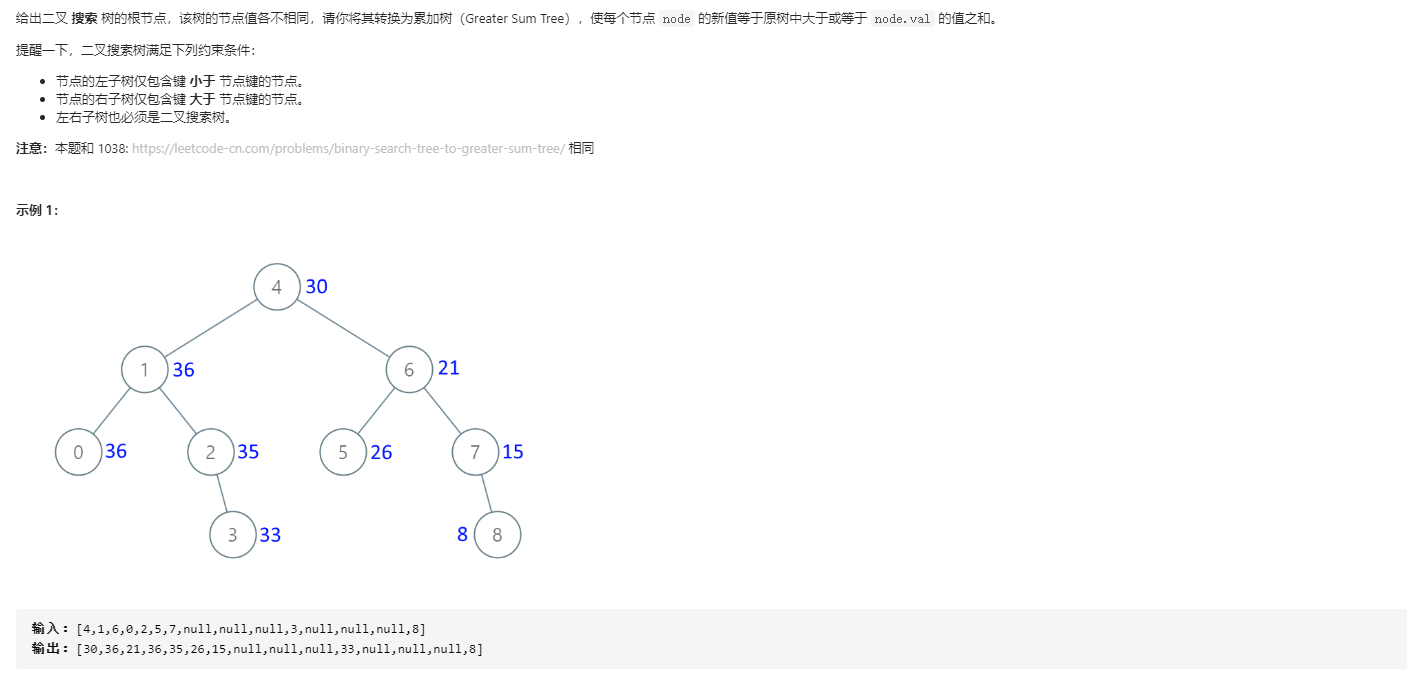
这个题虽然不难,但是值推导的时候还是容易出错。。。因为是二叉搜索树,所以大于当前节点的值都在右边,也就是中序遍历时在其后面的值都是大于当前值的,根据这个定理就可以得知中序遍历的时候进行累加,注意这个中序遍历先遍历右边,再遍历左边
public TreeNode convertBST(TreeNode root) { if(root == null) return null; dfs(root,0); return root; } public int dfs(TreeNode root,int val){ if (root == null)return val; int left = dfs(root.right,val); root.val = root.val+ left; int right = dfs(root.left, root.val); return right; }
623 在二叉树中新增一行

这题要注意圈起来的地方。。 不然一顿操作发上去错了还不知道为啥。。
public TreeNode addOneRow(TreeNode root, int v, int d) { if (root == null)return null; if (d == 1){ TreeNode tr = new TreeNode(v); tr.left = root; return tr; } LinkedList<TreeNode> stack = new LinkedList<>(); stack.addLast(root); int deep = 0; while (!stack.isEmpty()){ int size = stack.size(); deep++; for (int i = 0; i < size; i++) { TreeNode treeNode = stack.pollLast(); if (deep == d-1){ TreeNode left = new TreeNode(v); TreeNode right = new TreeNode(v); TreeNode ol = treeNode.left,or = treeNode.right; treeNode.left = left; treeNode.right = right; left.left = ol; right.right = or; }else { if (treeNode.left != null)stack.addFirst(treeNode.left); if (treeNode.right != null)stack.addFirst(treeNode.right); } } } return root; }
652 寻找重复的子树

这个关键点应该是一相同的子树 在加入null节点的时候 遍历的结果是唯一的 例如 ,这个前中后序遍历分别为 24,42,42 此时不能定位唯一二叉树,但是加入null节点后,前中后序的遍历结果就成了 24N,42N,4N2,我们用N表示null节点。所以就有了解决的方案
,这个前中后序遍历分别为 24,42,42 此时不能定位唯一二叉树,但是加入null节点后,前中后序的遍历结果就成了 24N,42N,4N2,我们用N表示null节点。所以就有了解决的方案
class Solution { Set<String> set ; Map<String,TreeNode> map; public List<TreeNode> findDuplicateSubtrees(TreeNode root) { List<TreeNode> result = new ArrayList<>(); if (root == null)return result; set = new HashSet<>(); map = new HashMap<>(); dfs(root); Set<String> keys = map.keySet(); for (String key : keys) { result.add(map.get(key)); } return result; } public String dfs(TreeNode root){ if (root == null)return "N"; String left = dfs(root.left); String right = dfs(root.right); String key = left+","+right+","+root.val; if (!set.contains(key)){ set.add(key); }else { map.put(key,root); } return key; } }
对了 在翻看评论的时候发现拼接字符串的解法复杂度是O(n^2) 而不是O(n) 这儿之所以是平方级别是因为每次拼接字符串的复杂度也是N
654 最大二叉树 这个题我想了一会儿,除了蛮干O(n^2)的复杂度 真的还没想到太好的办法,以为会涉及到归并法之类的。。结果没想到官解就是蛮干。。。真是心累。。这样的话就比较简单了。 只要不断递归区间,然后找最大值即可。。

public TreeNode constructMaximumBinaryTree(int[] nums) { return fill(nums,0,nums.length-1); } public TreeNode fill(int[] nums,int left,int right){ if (left==right)return new TreeNode(nums[left]); if (left>right)return null; int max = findMax(nums, left, right); TreeNode node = new TreeNode(nums[max]); node.left = fill(nums,left,max-1); node.right = fill(nums,max+1,right); return node; } public int findMax(int[] nums,int l,int r){ if (l>=r)return l; int max = l; for (int i = l+1; i <= r; i++) { if (nums[i]>nums[max]){ max = i; } } return max; }
662 二叉树的最大宽度

这题只要知道 index(node.left) = index(node)*2-1 index(node.right) = index(node)*2 就可以了
class Solution { Map<Integer,Integer> start; int max; public int widthOfBinaryTree(TreeNode root) { if(root == null) return 0; max = 1; start = new HashMap<>(); dfs(root,1,1); return max; } public void dfs(TreeNode node,int level,int val){ if (node == null)return; Integer value = start.get(level); if (value == null){ start.put(level,val); }else { max = Math.max(val-value+1,max); } level++; dfs(node.left,level+1,(val*2)-1); dfs(node.right,level+1,(val*2)); } }