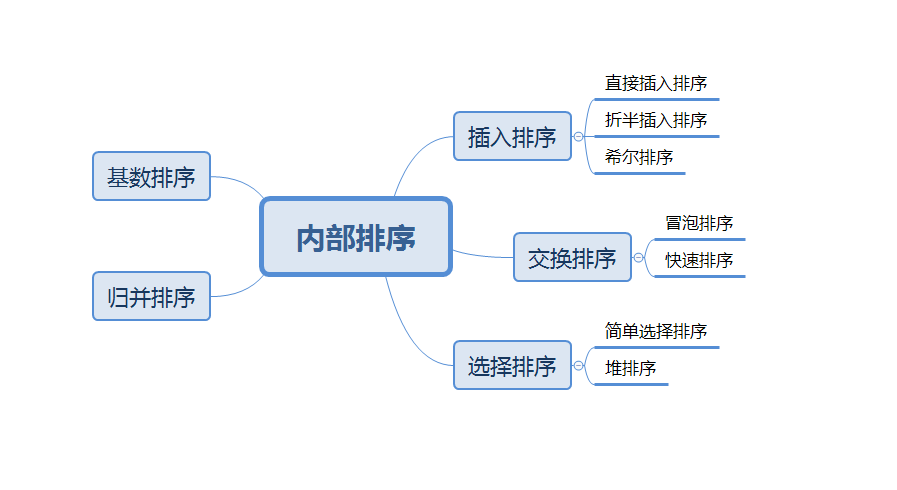
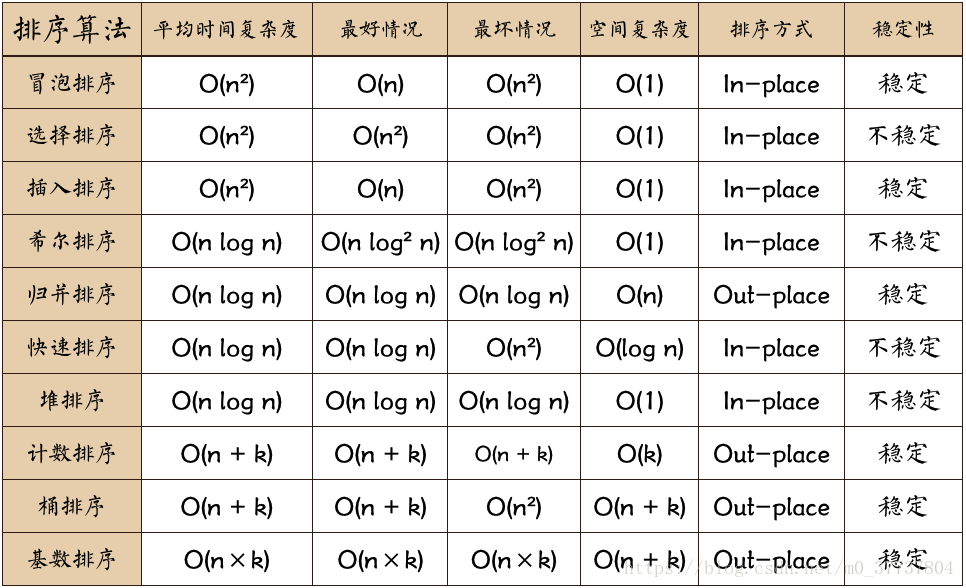
首先看一下内部排序分类以及各个算法的时间复杂度、空间复杂度和稳定性
一、插入排序
1、直接插入排序 (Straight Insertion Sort)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,将它插入到有序表中的适当位置,使之成为新的有序表,重复n-1次可完成排序过程。
步骤
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
代码:
方法一:

void InsertSort(ElemType A[],int n) { int i,j; //使用哨兵 for(int i = 2; i < n; i++) //依次将A[2]~A[n]插入到前面已排序序列; { if (A[i].key<A[i-1].key) //若A[i]的关键码小于其前驱,需将A[i]插入有序表 { A[0]<A[i]; //复制为哨兵,A[0]不存放元素 for(j=i-1;A[0].key<A[j].key;--j) //从后往前找待插入位置 { A[j+1]=A[j]; //向后挪位; } A[j+1]=A[0]; //复制到插入位置 } } }
方法2:

void insert_sort(int a[], int n) { int i, j, k; for (i = 1; i < n; i++) { //为a[i]在前面的a[0...i-1]有序区间中找一个合适的位置 for (j = i - 1; j >= 0; j--) if (a[j] < a[i]) break; //如找到了一个合适的位置 if (j != i - 1) { //将比a[i]大的数据向后移 int temp = a[i]; for (k = i - 1; k > j; k--) a[k + 1] = a[k]; //将a[i]放到正确位置上 a[k + 1] = temp; } } }
方法3:

def insert_sort(list): n = len(list) for i in range(1, n): # 后一个元素和前一个元素比较 # 如果比前一个小 if list[i] < list[i - 1]: # 将这个数取出 temp = list[i] # 保存下标 index = i # 从后往前依次比较每个元素 for j in range(i - 1, -1, -1): # 和比取出元素大的元素交换 if list[j] > temp: list[j + 1] = list[j] index = j else: break # 插入元素 list[index] = temp return list
2、直接插入排序的时间复杂度和稳定性
直接插入排序时间复杂度
直接插入排序的时间复杂度是O(N2)。
假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N),需要遍历多少次呢?N-1!因此,直接插入排序的时间复杂度是O(N2)。
直接插入排序稳定性
直接插入排序是稳定的算法,它满足稳定算法的定义。
算法稳定性 -- 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
3、代码实现
c:

#include <stdio.h> #include <stdlib.h> //直接插入排序 void InsertSort(int A[], int n) { int i, j, k; for (i = 1; i < n; i++) { //为a[i]在前面的a[0...i-1]有序区间中找一个合适的位置 for (j = i - 1; j >= 0; j--) if (A[j] < A[i]) break; //如找到了一个合适的位置 if (j != i - 1) { //将比a[i]大的数据向后移 int temp = A[i]; for (k = i - 1; k > j; k--) A[k + 1] = A[k]; //将a[i]放到正确位置上 A[k + 1] = temp; } } } //输出 void show_arr(int A[], int n) { int i = 0; for (i = 0; i < n;i++) { printf("%d ", A[i]); } } int main() { int sort_arr[9] = { 0,32, 34, 523, 53, 5, 65, 886, -35 }; int i, j; InsertSort(sort_arr, 9); show_arr(sort_arr, 9); system("pause"); return 0; }
python:

import numpy as np def insert_sort(list): for i in range(1,len(list)): #比较两个数值 if list[i] <list[i-1]: temp = list[i] index = i for j in range(i-1,-1,-1): if list[j]>temp: list[j+1] = list[j] index =j else: break list[index] = temp return list list = np.random.randint(1,100,10) print (insert_sort(list))
接着介绍排序算法——折半插入排序算法
一、概念
折半插入排序(binary insertion sort)是对插入排序算法的一种改进,由于排序算法过程中,就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度。
算法思想:在将一个新元素插入已排好序的数组的过程中,寻找插入点时,将待插入区域的首元素设置为a[low],末元素设置为a[high],则轮比较时将待插入元素与a[m],其中m=(low+high)/2相比较,如果比参考元素大,则选择a[low]到a[m-1]为新的插入区域(即high=m-1),否则选择a[m+1]到a[high]为新的插入区域(即low=m+1),如此直至low<=high不成立,即将此位置之后所有元素后移一位,并将新元素插入a[high+1]。
步骤
1、将待排序序列的第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
2、从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置,在查找元素的适当位置时,采用了折半查找方法。(如果待插入的元素与有序序列中的某个元 素相等,则将待插入元素插入到相等元素的后面。)
代码
方法一:
 View Code
View Code
方法二:
 View Code
View Code二、代码实现
C:
 View Code
View Codepython:

def binaryInsert(a): # 折半插入排序: 小->大 # 在直接插入排序的基础上使用了折半查找的方法 for i in xrange(1, len(a)): index = a[i] low = 0 hight = i - 1 while low <= hight: mid = (low + hight) / 2 if index > a[mid]: low = mid + 1 else: hight = mid - 1 # 跳出循环后 low, mid 都是一样的, hight = low - 1 for j in xrange(i, low, -1): a[j] = a[j - 1] a[low] = index return a
