如下找出该图的最小生成树
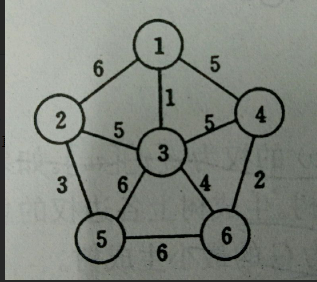
prim算法是求解该类问题的一种经典算法
Prim算法的基本思路:
将图中的所有的顶点分为两类:树顶点(已经被选入生成树的顶点)和非树顶点(还未被选入生成树的顶点)。首先选择任意一个顶点加入生成树,接下来要找出一条边添加到生成树,
这需要枚举每一个树顶点到每一个非树顶点所有的边,然后找到最短边加入到生成树。依次,重复操作n-1次,直到将所有顶点都加入生成树中。
算法实现如下
1 #include<bits/stdc++.h> 2 using namespace std; 3 void Prim(int n,int c[ ][100]) 4 { 5 int lowcost[100];//各非树顶点到树顶点集的最短路径 6 int closet[100];//非树顶点到树顶点集的最小边中相对的顶点 7 bool foot[n+1];//表示是否已经为树顶点,初始为false 8 memset(lowcost,0,sizeof(lowcost)); 9 memset(closet,0,sizeof(closet)); 10 foot[1]=true;//假设先把1作为初始顶点 11 for(int i=2;i<=n;i++){//假设从节点一开始 12 foot[i]=false; 13 closet[i]=1; 14 lowcost[i]=c[1][i]; 15 } 16 for(int i=1;i<n;i++){ 17 int min=99999; 18 int j=1; 19 for(int k=2;k<=n;k++){//计算非树顶点到树顶点集的最短路径,并把对应顶点记为j 20 if((lowcost[k]<min)&&(foot[k]==false)){ 21 min=lowcost[k]; 22 j=k; 23 } 24 } 25 cout <<"选边"<< "("<<closet[j] << "," <<j<<")" << endl;//把改变归为已选边,并把foot[j]设为true 26 foot[j]=true; 27 for(int k=2;k<=n;k++){//由于新的顶点加入树顶点,所以要更新非树顶点到树顶点集的最短路径lowcost[j],和对应的clost[j] 28 if((c[j][k]<lowcost[k])&&(foot[k]==false)){ 29 lowcost[k]=c[j][k]; 30 closet[k]=j; 31 } 32 } 33 } 34 35 36 } 37 int main() 38 { 39 cout << "请输入图的顶点数" << endl; 40 int n; 41 cin >>n; 42 cout << "请输入图的边数" << endl; 43 int m; 44 cin >> m; 45 cout << "请输入图的边的两个端点和边的长度" << endl; 46 int c[100][100]; 47 for(int i=1;i<=n;i++){ 48 for(int j=1;j<=n;j++){ 49 c[i][j]=99999; 50 } 51 } 52 int i1,j,k; 53 for(int i=1;i<=m;i++){ 54 cin >>i1 >> j >> k; 55 c[i1][j]=k; 56 c[j][i1]=k; 57 } 58 Prim(n,c); 59 return 0; 60 61 }
运行结果如下
