生成对抗网络GAN详细推导

转自：https://blog.csdn.net/ch18328071580/article/details/96690016

概述

1、什么是GAN？

生成对抗网络简称GAN，是由两个网络组成的，一个生成器网络和一个判别器网络。这两个网络可以是神经网络（从卷积神经网络、循环神经网络到自编码器）。我们之前学习过的机器学习或者神经网络模型主要能做两件事：预测和分类，这也是我们所熟知的。那么是否可以让机器模型自动来生成一张图片、一段语音？而且可以通过调整不同模型输入向量来获得特定的图片和声音。例如，可以调整输入参数，获得一张红头发、蓝眼睛的人脸，可以调整输入参数，得到女性的声音片段，等等。也就是说，这样的机器模型能够根据需求，自动生成我们想要的东西。因此，GAN 应运而生！

2、发展历史

生成对抗网络是由Ian Goodfellow等人于2014年在论文《Generative Adversarial Networks》中提出的。学术界公开接受了GAN，业界也欢迎GAN。GAN的崛起是不可避免的。

随着《Generative Adversarial Networks》提出后，GAN产生了广泛流行的架构，如DCGAN，StyleGAN，BigGAN，StackGAN，Pix2pix，Age-cGAN，CycleGAN。这些架构展示了非常有前途的结果。而随着GAN在理论与模型上的高速发展，它在计算机视觉、自然语言处理、人机交互等领域有着越来越深入的应用，并不断向着其它领域继续延伸。因此，本文将对GAN的理论与其应用做一个总结与介绍。

一、GAN模型

1、GAN的基本思想

GAN受博弈论中的零和博弈启发，将生成问题视作判别器和生成器这两个网络的对抗和博弈：生成器从给定噪声中（一般是指均匀分布或者正态分布）产生合成数据，判别器分辨生成器的的输出和真实数据。前者试图产生更接近真实的数据，相应地，后者试图更完美地分辨真实数据与生成数据。由此，两个网络在对抗中进步，在进步后继续对抗，由生成式网络得的数据也就越来越完美，逼近真实数据，从而可以生成想要得到的数据（图片、序列、视频等）。

如果将真实数据和生成数据服从两个分布，那么如图所示：

图中，蓝色虚线为判别分布D，黑色许虚线为真实的数据分布 P d a t a P_{data} Pdata​,绿色实线为生成分布 P g P_{g} Pg​。GAN从概率分布的角度来看，就是通过D来将生成分布推向真实分布，紧接着再优化D，直至到达图(d)所示，到达Nash均衡点，从而生成分布与真实分布重叠，生成极为接近真实分布的数据。

2、GAN的基本模型

以图片为例，真实图片集的分布 P d a t a ( x ) P_{data}{(x)} Pdata​(x)， x x x 是一个真实图片，可以想象成一个向量，这个向量集合的分布就是 P d a t a P_{data} Pdata​。我们需要生成一些也在这个分布内的图片，如果直接就是这个分布的话，很难做到。

现在有的 generator 生成的分布可以假设为 P G ( x ; θ ) P_G(x;θ) PG​(x;θ)，这是一个由 θ θ θ 控制的分布， θ θ θ 是这个分布的参数（如果是高斯混合模型，那么 θ θ θ 就是每个高斯分布的平均值和方差）。

假设在真实分布中取出一些数据， x 1 , x 2 , . . . , x m {x^1, x^2, ... , x^m} x1,x2,...,xm，我们想要计算一个似然 P G ( x i ; θ ) P_G(x^i; θ) PG​(xi;θ)。

对于这些数据，在生成模型中的似然就是：
L = ∏ i = 1 m P G ( x i ; θ ) L=prod _{i=1}^mP_G(x^i; heta) L=i=1∏m​PG​(xi;θ)

我们想要最大化这个似然，等价于让 generator 生成那些真实图片的概率最大。这就变成了一个最大似然估计的问题了，我们需要找到一个 θ ∗ θ^* θ∗ 来最大化这个似然。

寻找一个 θ* 来最大化这个似然，等价于最大化 log 似然。因为此时这 m 个数据，是从真实分布中取的，所以也就约等于，真实分布中的所有 x 在 P G P_G PG​分布中的 log 似然的期望。

真实分布中的所有 x 的期望，等价于求概率积分，所以可以转化成积分运算，因为减号后面的项和 θ 无关，所以添上之后还是等价的。然后提出共有的项，括号内的反转，max 变 min，就可以转化为 KL 散度的形式了，KL 散度描述的是两个概率分布之间的差异。

所以最大化似然，让 generator 最大概率的生成真实图片，也就是要找一个 θ 让 P G P_G PG​更接近于 P d a t a P_{data} Pdata​。

那如何来找这个最合理的 θ 呢？
我们可以假设 PG(x; θ) 是一个神经网络。

首先随机一个向量 z，通过 G ( z ) = x G(z)=x G(z)=x 这个网络，生成图片 x，如何比较两个分布是否相似呢？
只需要取一组样本 z，这组 z 符合一个分布，那么通过网络就可以生成另一个分布 P G P_G PG​，然后来比较与真实分布 P d a t a P_{data} Pdata​。

神经网络只要有非线性激活函数，就可以去拟合任意的函数。那么分布也是一样，所以可以用一个直正态分布，或者高斯分布，取样去训练一个神经网络，学习到一个很复杂的分布。

如何来找到更接近的分布，这就是 GAN 的贡献了。先给出 GAN 的公式：

这个式子的好处在于，固定 G G G， m a x V ( G , D ) max V(G,D) maxV(G,D) 就表示 P G P_G PG​ 和 P d a t a P_{data} Pdata​ 之间的差异。然后要找一个最好的 G G G，让这个最大值最小，也就是两个分布之间的差异最小。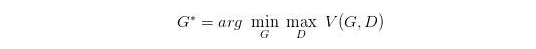

表面上看这个的意思是，对于判别器，D 要让这个式子尽可能的大，也就是对于 x 是真实分布中，D(x) 要接近与 1；对于 x 来自于生成的分布，D(x) 要接近于 0。
对于生成器来说，G 要让式子尽可能的小，让来自于生成分布中的 x，需要生成的数据尽量真，D(x) 尽可能的接近 1。

现在我们先固定 G，来求解最优的 D，也就是说，需要D越大越好：

对于一个给定的 x，得到最优的 D 如上，范围在 (0,1) 内，把最优的 D 带入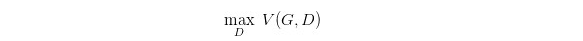

可以得到：

JS 散度 是 KL 散度 的对称平滑版本，表示了两个分布之间的差异，这个推导就表明了上面所说的，固定 G。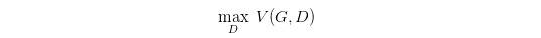

表示两个分布之间的差异，最小值是 − 2 l o g 2 -2log2 −2log2，最大值为 0。

现在我们需要找个 G G G，来最小化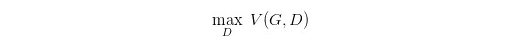

观察上式，当 P G ( x ) = P d a t a ( x ) P_G{(x)}=P_{data}(x) PG​(x)=Pdata​(x) 时，G 是最优的。

二、 GAN的训练

有了上面推导的基础之后，我们就可以开始训练 GAN 了。结合开头说的，两个网络交替训练，我们可以在起初有一个 G 0 G_0 G0​ 和 D 0 D_0 D0​，先训练 D 0 D_0 D0​ 找到 ：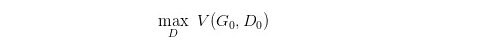

然后固定 D 0 D_0 D0​ 开始训练 G 0 G_0 G0​， 训练的过程都可以使用 gradient descent，以此类推，训练 D 1 D_1 D1​, G 1 G_1 G1​, D 2 D_2 D2​, G 2 G_2 G2​,…

但是这里有个问题就是，你可能在 D 0 ∗ D_0^* D0∗​ 的位置取到了：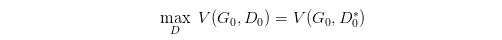

然后更新 G 0 G_0 G0​ 为 G 1 G_1 G1​，可能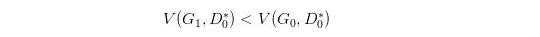

但是并不保证会出现一个新的点 D 1 ∗ D_1^* D1∗​使得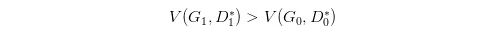

这样更新 G 就没达到它原来应该要的效果，如下图所示：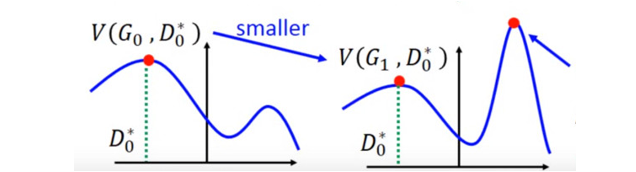

避免上述情况的方法就是更新 G 的时候，不要更新 G 太多。

知道了网络的训练顺序，我们还需要设定两个 loss function，一个是 D 的 loss，一个是 G 的 loss。下面是整个 GAN 的训练具体步骤：

上述步骤在机器学习和深度学习中也是非常常见，易于理解。

简单的来说，就是：

• 给定 G 0 G_0 G0​，最大化 V ( G 0 , D ) V(G_0,D) V(G0​,D) 以求得 D 0 ∗ D_0^* D0∗​，即 m a x [ J S ( P d a t a ( x ) ∣ ∣ P G 0 ( x ) ] max[JS(P_data(x)||P_G0(x)] max[JS(Pd​ata(x)∣∣PG​0(x)];
• 固定 D 0 ∗ D_0^* D0∗​，计算 θ G 1 θ_G1 θG​1 ← θ G 0 θ_G0 θG​0 − η ( d V ( G , D 0 ∗ ) / d θ G ) η(dV(G,D_0^*) /dθ_G) η(dV(G,D0∗​)/dθG​) 以求得更新后的 G 1 G_1 G1​；
• 固定 G 1 G_1 G1​，最大化 V ( G 1 , D 0 ∗ ) V(G_1,D_0^*) V(G1​,D0∗​) 以求得 D 1 ∗ D_1^* D1∗​，即 m a x [ J S ( P d a t a ( x ) ∣ ∣ P G 1 ( x ) ] max[JS(P_data(x)||P_G1(x)] max[JS(Pd​ata(x)∣∣PG​1(x)];
• 固定 D 1 ∗ D_1^* D1∗​，计算 θ G 2 θ_G2 θG​2 ← θ G 1 − η ( d V ( G , D 0 ∗ ) / d θ G ) θ_G1 −η(dV(G,D_0^*) /dθ_G) θG​1−η(dV(G,D0∗​)/dθG​) 以求得更新后的 G 2 G_2 G2​；
• 。。。

三、存在的问题

问题一

上面 G 的 loss function 还是有一点小问题，下图是两个函数的图像：

l o g ( 1 − D ( x ) ) log(1-D(x)) log(1−D(x)) 是计算时 G 的损失函数。但是，在 D(x) 接近于 0 的时候，这个函数十分平滑，梯度非常的小。这就会导致，在训练的初期，G 想要骗过 D，变化十分的缓慢，而上面的函数，趋势和下面的是一样的，都是递减的。但是它的优势是在 D(x) 接近 0 的时候，梯度很大，有利于训练，在 D(x) 越来越大之后，梯度减小，这也很符合实际，在初期应该训练速度更快，到后期速度减慢。

所以我们把 G 的 loss function 修改为：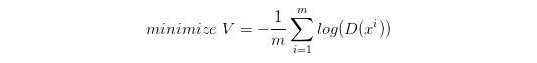

这样可以提高训练的速度。

问题二

还有一个问题，就是经过实验发现，经过许多次训练，loss 一直都是平的，也就是：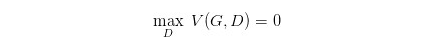

JS 散度一直都是 l o g 2 log2 log2， P G P_G PG​ 和 P d a t a P_{data} Pdata​ 完全没有交集，但是实际上两个分布是有交集的，造成这个的原因是因为，我们无法真正计算期望和积分，只能使用 sample 的方法，如果训练的过拟合了，D 还是能够完全把两部分的点分开，如下图：

对于这个问题，我们是否应该让 D 变得弱一点，减弱它的分类能力，但是从理论上讲，为了让它能够有效的区分真假图片，我们又希望它能够 powerful，所以这里就产生了矛盾。

还有可能的原因是，虽然两个分布都是高维的，但是两个分布都十分的窄，可能交集相当小，这样也会导致 JS 散度算出来 = l o g 2 =log2 =log2，约等于没有交集。

解决的一些方法，有添加噪声，让两个分布变得更宽，可能可以增大它们的交集，这样 JS 散度就可以计算，但是随着时间变化，噪声需要逐渐变小。

问题三

还有一个问题叫 Mode Collapse，如下图：

这个图的意思是，data 的分布是一个双峰的，但是学习到的生成分布却只有单峰，我们可以看到模型学到的数据，但是却不知道它没有学到的分布。

造成这个情况的原因是，KL 散度里的两个分布写反了

这个图很清楚的显示了，如果是第一个 KL 散度的写法，为了防止出现无穷大，所以有 P d a t a P_{data} Pdata​ 出现的地方都必须要有 P G P_G PG​ 覆盖，就不会出现 Mode Collapse。