12.1目标优化
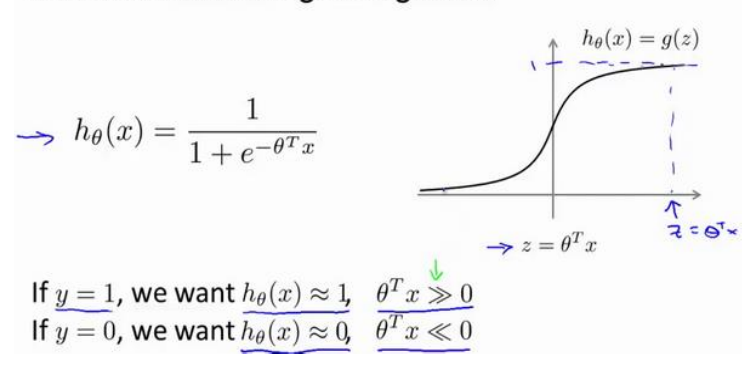
（1）以下是逻辑回归以及单个样本的代价函数
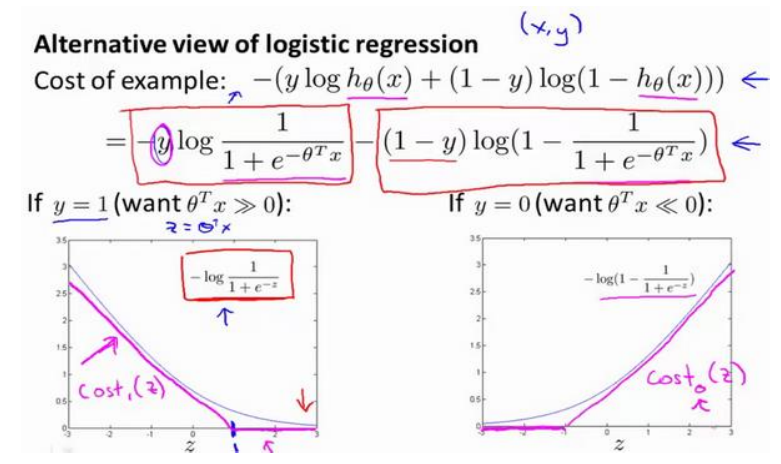
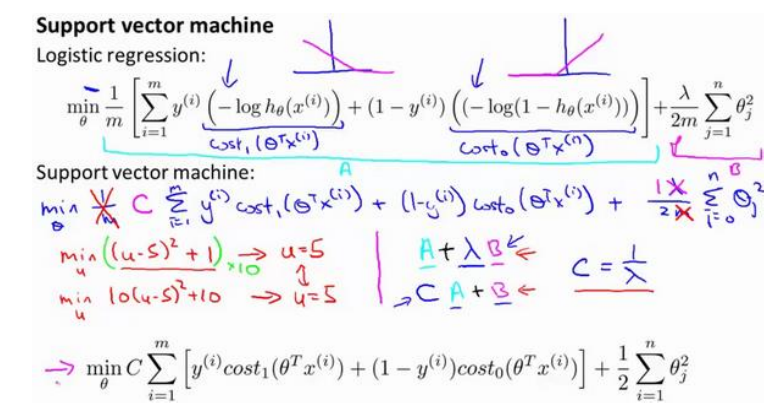
（2）首先将使用上图中紫色的线（称为cost1或者cost0）的代替曲线，然后将样本数m去掉，最后将C代替1/λ（可以这么理解，但不完全是），从而实现逻辑回归的代价函数到SVM的转换。
（3）SVM的输出将不再是逻辑回归的概率，而就是0或者1：
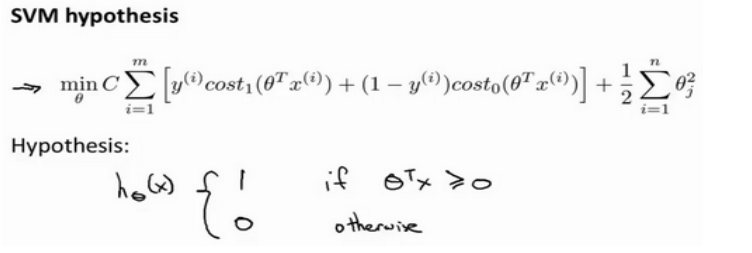
12.2大边界的直观理解
（1）首先对z的要求更加严格了，在逻辑回归中只要求大于或小于零，，这里将会是大于等于1或小于等于-1。
（2）假设C非常大时，我们的优化会尽量时第一项为零，假设可以得到这样的参数，那么就可以将代价函数转换为：
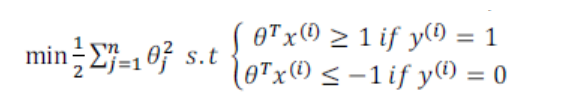
即在后面的约束下求解前面的最小值。
（3）C非常大时（即λ非常小），会尽量去满足上面的约束，这样会导致对异常点非常敏感（过拟合），如下所示：
这时将会得到紫色的线，如果将C适当减小，会得到满意的黑色线的。即C不那么大时，可以忽略掉一些异常点。
C是惩罚系数，理解为调节优化方向中两个指标（间隔大小，分类准确度）偏好的权重，即对误差的宽容度，C越高，说明越不能容忍出现误差,容易过拟合，C越小，容易欠拟合，C过大或过小，泛化能力变差。
（3）支持向量机经常被称为最大间距分类器，在C很大时确实如此，但C不是那么大时，将不是，如上一点的例子所示。但是这么理解是有助于理解SVM的。
（4）C较大相当于λ较小，会出现过拟合；反之则出现欠拟合。
12.3数学背后的最大边界分类（选修）
（1）向量的内积：一个向量投影到另一个向量投影长度与向量的范数的乘积，也就是对应坐标相乘再相加。
（2）目标函数要使得θ尽可能小，这时只要使得x在θ上的投影尽可能的大，就能够在θ取越小的值时满足约束条件，这就是SVM背后的数学原理。
（3）θ和边界呈现90°垂直，另外θ0为零时边界通过原点，反之不通过原点。
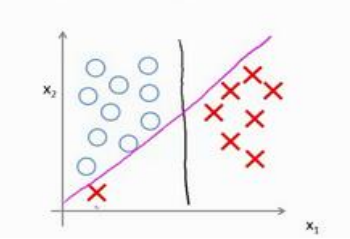
12.4核函数1
（1）如果直接用多项式取拟合下面的边界的话，肯能需要多项式的次数很高，特征很多。
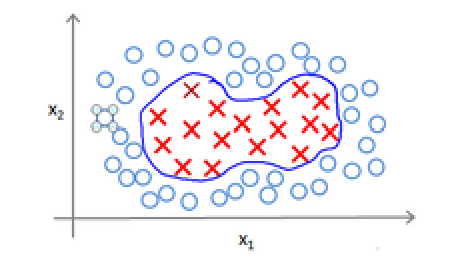
（2）利用x的各个特征与我们预先选定地标（landmark）l（1），l（2），l（3），的近似程度选取新的特征f1,f2,f3。
上面是一个高斯核函数，注：这个函数与正态分布没什么实际上的关系，只是看上去像而已。
（3）与地标越近结果f越接近1，越远f越接近0。
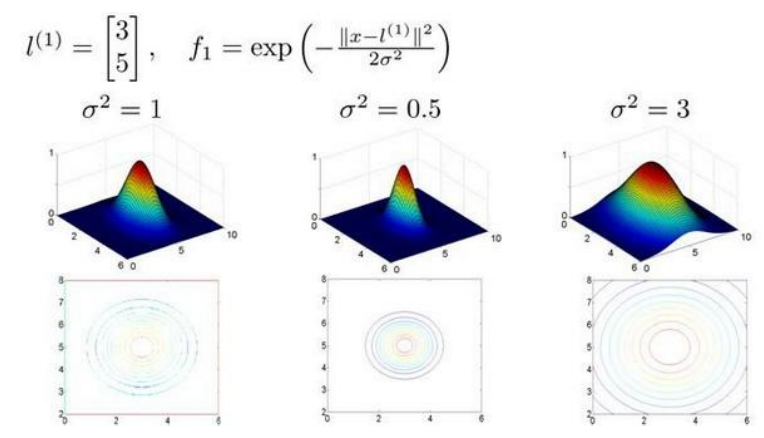
（3）通过一下式子将很容易进行分类：
（4）核函数计算的结果即为新的特征。
12.5核函数2
（1）地标的个数设置为样本数m,即每个样本的位置即为地标的位置：
（2）将核函数运用到支持向量机中，
给定x,计算新特征f,当θTf>0时，预测y=1，否则反之。
相应的修改代价函数为：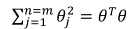
在具体实施过程中，还需要对最后的正则化想微调，在计算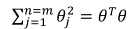时，用θTMθ代替θTθ。M跟选择的核函数有关，用相关库几块使用带核函数的SVM。
不带核函数的SVM称为线性核函数。
（3）以下是支持向量机的两个参数C和σ的影响：
C=1/λ；
C较大时，相当于λ较小，可能会导致过拟合，高方差；
C较小时，相当于λ较大，可能会导致欠拟合，高偏差；
σ较大时，可能会导致低方差，高偏差。
σ较小时，可能会导致低偏差，高方差。
12.6使用支持向量机
（1）尽管不需要自己去写SVM函数，直接使用相关库，但需要做一下几件事：
1.是提出参数C的选择。在之前视频中已经讨论了C对方差偏差的影响。
2.选择内核参数或你想要使用的相似函数。
（2）以下是逻辑回归和支持向量机的选择：
1.相比于样本数m，特征数n大的多的时候，没有那么多数据量去训练一个非常复杂的模型，这时考虑用SVM。
2.如果n较小，而且m大小中等，例如n在1-1000之间，而m在10-1000之间，使用高斯函数的支持向量机。
3.如果n较小，而m较大，例如n在1-1000之间，而m大于50000，则使用支持向量机会非常慢，解决方案是创造增加更多的特征，然后使用逻辑回归或不带核函数的支持向量机。
神经网络在以上三种情况下都可以有较好的表现，但神经网络训练可能非常慢，选择支持向量机的原因主要在于它的代价函数是凸函数，不存在局部最小值。