具体问题如下图

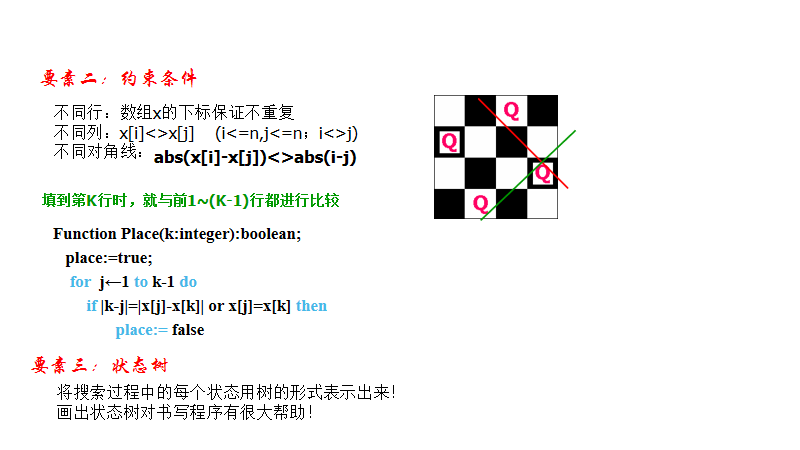
先看一下4*4的回溯过程
程序结束条件: 一组解:设标志,找到一解后更改标志,以标志做为结束循环的条件。 所有解:k=0
判断约束函数判断第k个后能不能放在x[k]处 两个皇后不能放在统一斜线上: 若2个皇后放置的位置分别是(i,j)和(k,l), 且 i-j = k -l 或 i+j = k+l,则说明这2个皇后处于同一斜线上。
下面是利用递归和非递归实现的代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n; 4 int x[100]; 5 int sum=0; 6 7 /* 8 判断第k个后能不能放在x[k]处 9 两个皇后不能放在统一斜线上: 10 若2个皇后放置的位置分别是(i,j)和(k,l), 11 且 i-j = k -l 或 i+j = k+l,则说明这2个皇后处于同一斜线上。 12 */ 13 void output(){ 14 cout << "第" <<sum << "种放置方法为:" << endl; 15 for(int i=1;i<=n;i++){ 16 cout << "(" <<i << "," << x[i] << ")" << endl; 17 } 18 19 } 20 int place(int k){ 21 for(int j=1;j<k;j++){ 22 if(x[j]==x[k] || abs(x[j]-x[k])== abs(j-k)) 23 return 0; 24 } 25 return 1; 26 } 27 void BackTrace(int t,int n){//递归 28 if(t>n){////如果t>n说明已经完成一次放置 29 sum++; 30 output(); 31 } 32 else{ 33 for(int i=1;i<=n;i++){ 34 x[t]=i; 35 if(place(t)){// //可以放在i位置处,则继续搜索 36 BackTrace(t+1,n); 37 } 38 } 39 40 } 41 } 42 43 void BackTrace1(int n){//非递归 44 int k; 45 x[1]=0; 46 k=1; 47 while(k>=1){ 48 x[k]+=1;////先放在第一个位置 49 while((x[k]<=n && !(place(k)))){//如果不能放 50 x[k]++;// //放在下一个位置 51 } 52 if(x[k]<=n){ 53 if(k==n){// //如果已经放完了n个皇后 54 sum++; 55 output(); 56 } 57 else{// //没有处理完,让k自加,处理下一个皇后 58 k++; 59 x[k]=0; 60 } 61 }else{// 当前无法完成放置,则进行剪枝,回溯回去,回到第k-1步 62 k--; 63 } 64 } 65 } 66 int main() 67 { 68 memset(x,0,sizeof(x)); 69 cin >> n; 70 cout << n << "皇后的放置方法为" << endl; 71 //BackTrace(1,n); 72 BackTrace1(n); 73 return 0; 74 }
运行结果如下
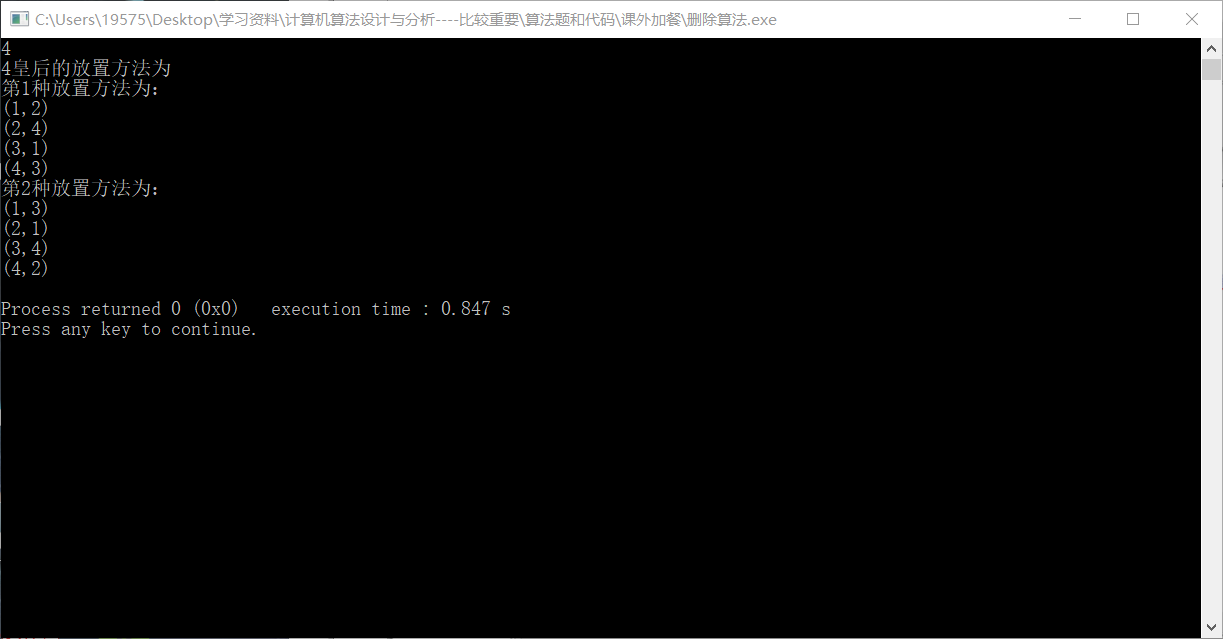
皇后个数要大于3才有可行结