手撸机器学习算法

系列文章目录：

• 感知机
• 线性回归
• 非线性问题
• 多项式回归
• 岭回归

感知机（Perceptron）是最最最简单的机器学习算法（分类），同时也是深度学习中神经元的基础组件；

算法介绍

感知机与逻辑回归、SVM类似的是同样是构建一个分割超平面来实现对数据点的分类，不同点在于超平面的查找过程更加的简单粗暴，简单介绍下它的算法流程：

1. 假设二分类线性可分问题，x为输入特征，y为输出标签，y取值为-1和+1；
2. 随机超平面变量，由超平面公式(w*x+b)，x为输入数据点，不用管它，因此也就是w和b需要随机初始化；
3. 遍历所有数据点，判断该点在当前超平面下的分类是否准确，可以通过(w*x_i+b)与(y_i)的乘积来判断，如果二者乘积大于0，说明二者符号一致，即分类正确，反之分类错误；
4. 如果分类错误，则需要更新w和b，更新公式为：(w=w+y_i*x_i)，(b=y_i+b)，这个公式可以这样理解，对于w来说，需要更新说明(w*x_i+b)与(y_i)的乘积小于0，假设(y_i)为-1，则(w*x_i+b)大于0，此时我们希望能减小(w*x_i+b)，此时(w=w+y_i*x_i)等价于(w=w-x_i)，因此满足调整需求；
5. 重复上述2，3，4步骤，直到所有点都分类正确为止；

代码实现

构建数据集

注意由于感知机只能处理线性可分的情况，因此下面数据集需要满足线性可分，否则迭代过程无法终止；

X = np.array([[5,2], [3,2], [2,7], [1,4], [6,1], [4,5]])
Y = np.array([-1, -1, 1, 1, -1, 1])

随机变量初始化

这里的初始化值也是随机的，对于w，由于输入X是二维的，因此它也需要是二维的；

w,b = np.array([0, 0]),0

遍历数据集及更新参数

run = True
while run:
    run = False
    for x,y in zip(X,Y):
        if y*(np.dot(w,x)+b)<=0:
            w,b = w+y*x,y+b
            run = True
            break

运行结果

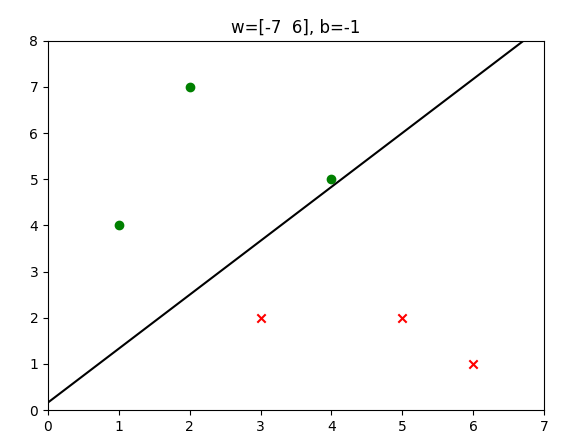
完整代码

import numpy as np
import matplotlib.pyplot as plt

'''
感知机：线性二分类模型，拟合分割超平面对数据进行分类；
暴力实现：无脑针对每一个错误点进行w和b的更新，可以证明在线性可分情况下，有限次迭代可以完成划分；
'''

# 初始化 w 和 b，np.array 相当于定义向量
w,b = np.array([0, 0]),0 

# 定义 d(x) 函数
def d(x):
    return np.dot(w,x)+b # np.dot 是向量的点积

# 历史信用卡发行数据
# 这里的数据集不能随便修改，否则下面的暴力实现可能停不下来
X = np.array([[5,2], [3,2], [2,7], [1,4], [6,1], [4,5]])
Y = np.array([-1, -1, 1, 1, -1, 1])

run = True
while run:
    run = False
    for x,y in zip(X,Y):
        if y*d(x)<=0:
            w,b = w+y*x,y+b
            run = True
            break

print(w,b)

positive = [x for x,y in zip(X,Y) if y==1]
negative = [x for x,y in zip(X,Y) if y==-1]
line = [(-w[0]*x-b)/w[1] for x in [-100,100]]
plt.title('w='+str(w)+', b='+str(b))
plt.scatter([x[0] for x in positive],[x[1] for x in positive],c='green',marker='o')
plt.scatter([x[0] for x in negative],[x[1] for x in negative],c='red',marker='x')
plt.plot([-100,100],line,c='black')
plt.xlim(min([x[0] for x in X])-1,max([x[0] for x in X])+1)
plt.ylim(min([x[1] for x in X])-1,max([x[1] for x in X])+1)

plt.show()

最后

从算法上看，感知机无疑是非常简单的一种，但是它的训练过程依然是完整的，因此作为机器学习入门算法非常合适，尤其是在后续很多算法甚至是深度学习中都能看到它的影子；