先明确欧拉函数:计算任意给定的正整数n,在小于等于n的正整数中和n构成互质关系的正整数个数,比如φ(8) = 4,因为1,3,5,7都与8互质
性质1:n=1时,φ(1) = 1;
性质2:如果n是质数,那么φ(n) = n-1,因为质数与小于它的每一个数都构成质数关系
性质3:如果 n = p^k(p为质数,k>=1),则满足以下公式,比如 φ(8) = φ(2^3) =2^3 - 2^2 = 8 -4 = 4。当一个数不包含质数p,才可能与n互质,而包含质数p的数一共有p^(k-1)个,即1×p、2×p、3×p、…、p^(k-1)×p,把它们去除,剩下的就是与n互质的数。
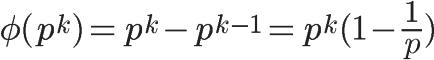 第二种情况可以看成k=1的特解。
第二种情况可以看成k=1的特解。
性质4:如果n可以分解成两个互质整数的乘积,n = p1 × p2,则φ(n) = φ(p1p2) = φ(p1)φ(p2),比如φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24
性质5:由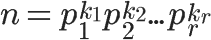 可以得到
可以得到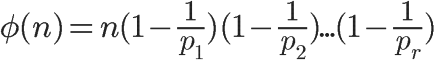
推论:对于互质的数p、n,满足p^(φ(n)+1) ≡ p (mod n)
欧拉公式的延伸:小于n 与n互质的数的和 是euler(n)*n/2
求某个数字n的欧拉函数值:时间复杂度O(n*n)
int getphi(int n) { int i,ans; ans = m = n; for(i = 2; i*i <= m; i ++) { if(n%i == 0) { ans = ans/i*(i-1); while(n%i == 0) n/=i; } } if(n > 1) ans = ans/n*(n-1); return ans; }
欧拉筛法求1~n的欧拉函数值:时间复杂度O(n)
void euler()
{
ans = 0;
memset(book,0,sizeof(book));
p[1] = 1;
int i,j;
for(i = 2; i <= n; i ++)
{
if(!book[i])
{
prime[ans++] = i;
p[i] = i-1;//性质2的应用
}
for(j = 0; j < ans&&i*prime[j] < n; j ++)
{
book[i*prime[j]] = 1;
if(i%prime[j] == 0)//如果i和它的最小质数构成互质关系
{
p[i*prime[j]] = p[i]*p[prime[j]];//性质4和性质5的应用
break;
}
else
p[i*prime[j]] = p[i]*(p[prime[j]]-1);//性质2和性质4的应用
}
}
return;
}