题目大意:
给出个的开关,按下一个开关会影响周围4个灯和自己(开变成关,关变成开)。求最少需要按多少次开关才能使得全部灯变亮?(6次以上则视为无法点亮)。
思路:
这道题如果用普通的广搜会T。。。
这道题的正解如下:
假设我们不动第一行的开关,那么如果要改变第一行的灯的状态,那么就只能更改第二行的位于该灯下面的那个开关来改变。例如:
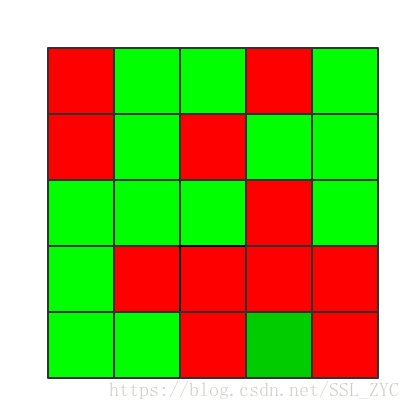
如果我们固定了第一行,那么为了将全部都变成绿色,就必须利用第二行。例如,是红色,为了让它变成绿色,就必须更改。为了让变成绿色,就必须更改。
更改后图形如下:
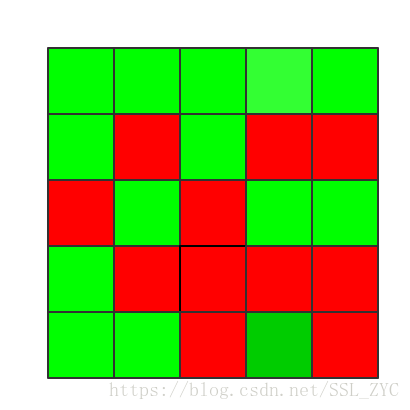
那么我们再固定第二行,利用第三行来更改它(就像用第一行来更改第二行一样),就变成了
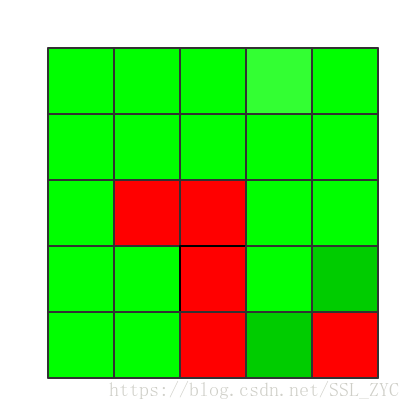
同理,更改第三行
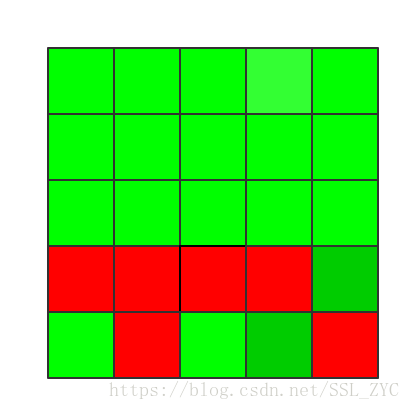
再更改第四行
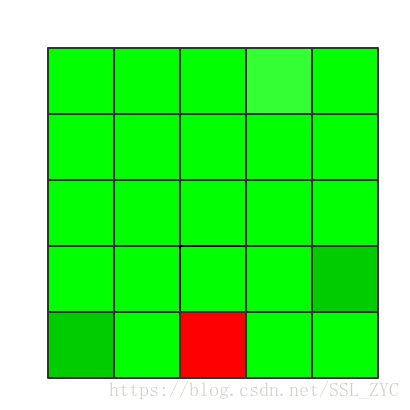
这是我们发现,最后还有一个灯是关着的,所以,这说明第一行的灯如果是这样的情况就无法成立
那么就枚举第一行的点击方式,再继续按照刚才的方法,判断能否点玩即可。
代码:
#include <cstdio>
#include <iostream>
#define Inf 1e7
using namespace std;
int n,a[6][6],b[6][6],ans;
int check(int x) //判断当第一行的情况是否成立
{
int sum=x;
for (int i=1;i<=5;i++)
for (int j=1;j<=5;j++)
b[i][j]=a[i][j];
for (int i=1;i<=4;i++)
for (int j=1;j<=5;j++)
if (!b[i][j]) //第i行是关灯
{
sum++; //记录次数
b[i][j]=1-b[i][j];
b[i+1][j]=1-b[i+1][j];
b[i+1][j-1]=1-b[i+1][j-1];
b[i+1][j+1]=1-b[i+1][j+1];
b[i+2][j]=1-b[i+2][j];
}
for (int i=1;i<=5;i++)
if (!b[5][i]) return Inf; //判断最后一行是否全开
return sum;
}
void dfs(int x,int k) //枚举第一行的情况
{
if (x>5) //第一行更改完毕
{
ans=min(ans,check(k));
return;
}
a[1][x]=1-a[1][x];
a[1][x-1]=1-a[1][x-1];
a[1][x+1]=1-a[1][x+1];
a[2][x]=1-a[2][x];
dfs(x+1,k+1); //按这个开关
a[1][x]=1-a[1][x];
a[1][x-1]=1-a[1][x-1];
a[1][x+1]=1-a[1][x+1];
a[2][x]=1-a[2][x];
dfs(x+1,k); //不按这个开关
return;
}
int main()
{
scanf("%d",&n);
while (n--)
{
for (int i=1;i<=5;i++)
for (int j=1;j<=5;j++)
scanf("%1d",&a[i][j]);
ans=Inf;
dfs(1,0);
if (ans<7) printf("%d\n",ans);
else printf("-1\n");
}
return 0;
}