题目大意:
小T是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有这批矿产共有个矿石,从到逐一编号,每个矿石都有自己的重量以及价值。检验矿产的流程是:
- 给定个区间
- 选出一个参数
- 对于一个区间,计算矿石在这个区间上的检验值:
这批矿产的检验结果为各个区间的检验值之和。若这批矿产的检验结果与所给标准值相差太多,就需要再去检验另一批矿产。小T不想费时间去检验另一批矿产,所以他想通过调整参数的值,让检验结果尽可能的靠近标准值,即使得的绝对值最小。请你帮忙求出这个最小值。
思路:
首先不考虑最小值,设表示为时最终的值。当的值增大时,显而易见时增大的。所以这是一个单调上升的序列,即

假定的位置
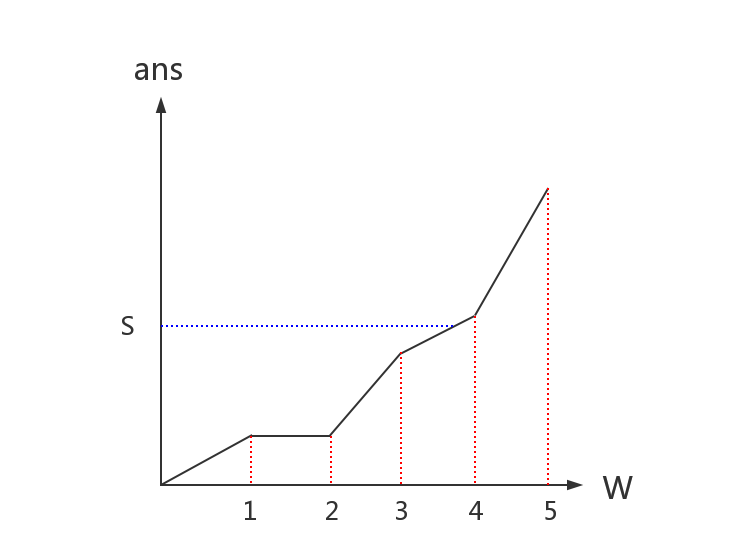
那么答案肯定就是选择或了。
如何得到的呢?
很明显,就是二分出第一个ans不超过s的位置,就是二分出第一个ans不少于s的位置!
然后只要在和中取一个最小值就可以了。
每次前缀和求出,再套上二分答案,时间复杂度,其中定值为。
代码:
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N=200010;
int n,m,l,r,mid,w[N],v[N],x[N],y[N];
ll s,ans,minn1,minn2,Read;
char ch;
ll read()
{
Read=0;
ch=getchar();
while (ch<'0'||ch>'9') ch=getchar();
while (ch>='0'&&ch<='9')
Read=(Read<<3)+(Read<<1)+ch-48,ch=getchar();
return Read;
}
struct node
{
ll v,s;
}sum[N];
ll ask(int h)
{
ans=0;
sum[0].s=sum[0].v=0;
for (int i=1;i<=n;i++)
if (w[i]>=h) //不小于W
{
sum[i].s=sum[i-1].s+1; //个数
sum[i].v=sum[i-1].v+(ll)v[i]; //价值
}
else
{
sum[i].s=sum[i-1].s;
sum[i].v=sum[i-1].v;
}
for (int i=1;i<=m;i++)
ans+=(ll)(sum[y[i]].s-sum[x[i]-1].s)*(ll)(sum[y[i]].v-sum[x[i]-1].v); //枚举区间求ans
return ans;
}
int main()
{
n=read(),m=read(),s=read();
for (int i=1;i<=n;i++)
w[i]=read(),v[i]=read();
for (int i=1;i<=m;i++)
x[i]=read(),y[i]=read();
minn1=minn2=1e17;
l=0;
r=1000000;
while (l<=r)
{
mid=(l+r)/2;
if (ask(mid)>=s) l=mid+1;
else r=mid-1;
}
minn1=ask(l-1);
l=0;
r=1000000;
while (l<=r)
{
mid=(l+r)/2;
if (ask(mid)<=s) r=mid-1;
else l=mid+1;
}
minn2=ask(r+1);
cout<<min(abs(minn1-s),abs(minn2-s));
return 0;
}