【洛谷P2607】骑士【基环树】【dp】

题目大意：

题目链接：https://www.luogu.org/problemnew/show/P2607
有$n$个骑士，每个骑士有自己最讨厌的人和战斗力，一个骑士不肯与自己讨厌的人一起加入队伍。求最大战斗力和。

---

思路：

双倍经验 P1453 城市环路
一开始没有看出来就是没有上司的舞会那道题啊。用自己的方法做的。
这道题是一个基环树森林，所以拆成每一个基环树来做。
对于任意一棵基环树，它的长相是这样的。

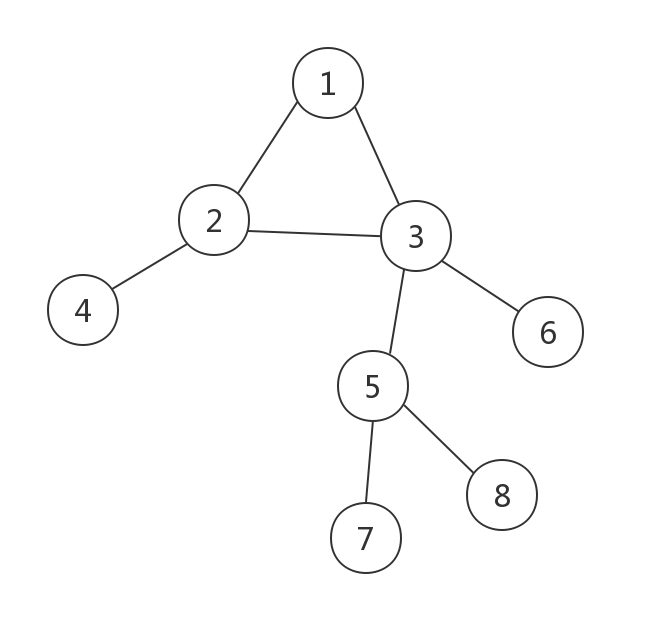
先找到环

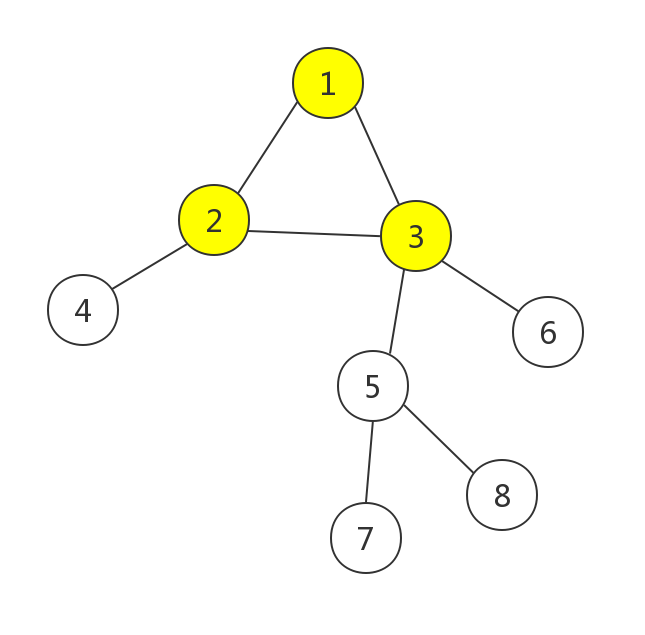
然后对于环上的每一个节点为根，求出在其子树内的最大攻击力。
设$f[x][0/1]$表示在以节点$x$为根的子树内，不选或者选点$x$的最大攻击力。那么明显方程为
$f[x][1]=(sum f[y][0](yin son[x]))+a[x]$
$f[x]][0]=sum max(f[y][0],f[y][1])(yin son[x]))$
其中$a[x]$表示$x$的攻击力。
那么接下来就要处理环上的点了。
由于环上的点$1$和点$cnt$是不可以同时选择的（$cnt$表示换上的点的个数），所以这次就多设一维，$g[i][0/1][0/1]$表示环上的第$i$个点 不选/选 ,且第一个点 不选/选 的最大攻击力。

• 那么对于第1个点不选的情况，要初始化好$g[2]$，其方程为
  $g[i][0][0]=max(g[i-1][1][0],g[i-1][0][0])+f[Q[i]][0]$
  $g[i][1][0]=g[i-1][0][0]+f[Q[i]][1]$
  其中$Q[i]$表示环上的第$i$个点。
• 对于选择第一个点的情况，第二个点一定不能选。所以初始化好$g[2],g[3]$。（$g[2]$不可以不初始化，虽然在转移过程中起不到作用，但是如果这个环上只有两个点的话，不初始化$g[2]$就没办法输出$g[2]$的答案），其方程为
  $g[i][0][1]=max(g[i-1][1][1],g[i-1][0][1])+f[Q[i]][0]$
  $g[i][1][1]=g[i-1][0][1]+f[Q[i]][1]$
  由于最终答案中$1$和$cnt$不可以同时选择，所以答案就是$max(g[cnt][1][0],g[cnt][0][0],g[cnt][0][1])$

时间复杂度$O(n)$，跑的比较慢，需要进行优化。

---

代码：

#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define rr register
using namespace std;
typedef long long ll;

const int N=1000010;
int n,x,tot,cnt,head[N],a[N],in[N],Q[N];
ll f[N][2],g[N][2][2],ans;
bool vis[N],ok;

struct edge
{
    int next,to;
}e[N*2];

ll maxx(ll x1,ll x2,ll x3)
{
    return max(x1,max(x2,x3));
}

int read()
{
	int d=0;
	char ch=getchar();
	while (ch<'0'||ch>'9') ch=getchar();
	while (ch>='0'&&ch<='9') 
		d=(d<<3)+(d<<1)+ch-48,ch=getchar();
	return d;
}

void add(int from,int to)
{
    e[++tot].to=to;
    e[tot].next=head[from];
    head[from]=tot;
}

void topsort()  //拓扑排序找环
{
    queue<int> q;
    for (rr int i=1;i<=n;i++)
        if (in[i]==1) q.push(i);
    while (q.size())
    {
        int u=q.front(),v;
        q.pop();
        for (rr int i=head[u];~i;i=e[i].next)
        {
            v=e[i].to;
            if (in[v]>1)
            {
                in[v]--;
                if (in[v]==1) q.push(v);
            }
        }
    }
}

void find(int x)  //寻找环上的点
{
    vis[x]=1; 
    Q[++cnt]=x;
    for (rr int i=head[x];~i;i=e[i].next)
    {
        int y=e[i].to;
        if (!vis[y]&&in[y]>=2) find(y);
    }
}

void dp(int x)  //求非环上的点的最大攻击力
{
    vis[x]=1;
    f[x][1]=(ll)a[x];
    for (rr int i=head[x];~i;i=e[i].next)
    {
        int y=e[i].to;
        if (!vis[y]&&in[y]<=1)
        {
            dp(y);
            f[x][1]+=f[y][0];
            f[x][0]+=max(f[y][0],f[y][1]);
            ok=1;
        }
    }
}

int main()
{
    memset(head,-1,sizeof(head));
    n=read();
    for (rr int i=1;i<=n;i++)
    {
        a[i]=read(),x=read();
        add(x,i);
        add(i,x);
        in[i]++;  //这个点的度数
        in[x]++;
    } 
    topsort();
    for (rr int k=1;k<=n;k++)
        if (in[k]>=2&&!vis[k])
        {
            memset(Q,0,sizeof(Q));
            memset(g,0,sizeof(g));
            cnt=0;
            find(k);
            for (rr int i=1;i<=cnt;i++)
                dp(Q[i]);
            g[2][1][0]=f[Q[1]][0]+f[Q[2]][1];
            g[2][0][0]=f[Q[1]][0]+f[Q[2]][0]; 
            for (rr int i=3;i<=cnt;i++)
            {
                g[i][0][0]=max(g[i-1][1][0],g[i-1][0][0])+f[Q[i]][0];
                g[i][1][0]=g[i-1][0][0]+f[Q[i]][1];
            }
            g[2][0][1]=f[Q[1]][1]+f[Q[2]][0];
            g[3][0][1]=f[Q[1]][1]+f[Q[2]][0]+f[Q[3]][0];
            g[3][1][1]=f[Q[1]][1]+f[Q[2]][0]+f[Q[3]][1];
            for (rr int i=4;i<=cnt;i++)
            {
                g[i][0][1]=max(g[i-1][1][1],g[i-1][0][1])+f[Q[i]][0];
                g[i][1][1]=g[i-1][0][1]+f[Q[i]][1];
            }
            ans+=maxx(g[cnt][1][0],g[cnt][0][0],g[cnt][0][1]);
        }
    printf("%lld",ans);
    return 0;
}