SVM的推导和理解

主要记录了SVM思想的理解,关键环节的推导过程,主要是作为准备面试的需要.

1.准备知识-点到直线距离

点(x_0)到超平面(直线)(w^Tx+b=0)的距离,可通过如下公式计算:

[d = frac{w^Tx_0+b}{||w||} ]

因为公式分子部分没有带绝对值,因此计算得到的d有正负之分.因为超(w^Tx+b=0)将空间分为两部分(以2维为例,直线(w_1x+w_2y+b=0),将二维空间划分为上下两部分),其中一部分d大于0,另一部分d小于0.

上面距离公式的简单推导过程如下:

1. 超平面(w^Tx+b=0)的一个法向量为(w):
   因为对于超平面上任意不同的两点(x_0,x_1),他们所构成的向量((x_1-x_0)),与(w)的内积为:

[egin{align} w^T(x_1-x_0) &= w^Tx_1-w^Tx_0\ &= -b-(-b)\ &= 0 end{align}]

即,(w)与超平面上任意向量(直线)正交,即(w)为超平面的法向量,(frac{w}{||w||})为超平面的单位法向量.
2. 点(x_0)到超平面(w^Tx+b=0)的距离等于,平面上任意一点(x_1)与点(x_0)构成的向量在单位法向量上的投影,即:

[egin{align} d &= frac{w^T(x_0-x_1)}{||w||}\ &= frac{w^Tx_0-w^Tx_1}{||w||}\ &= frac{w^Tx_0-(-b)}{||w||}\ &= frac{w^Tx_0+b}{||w||}\ end{align}]

2. 支持向量机的数学表示

SVM的图示如下,主要思想是寻找使得margin最大的超平面,该超平面为两条平行的边界超平面的中心.

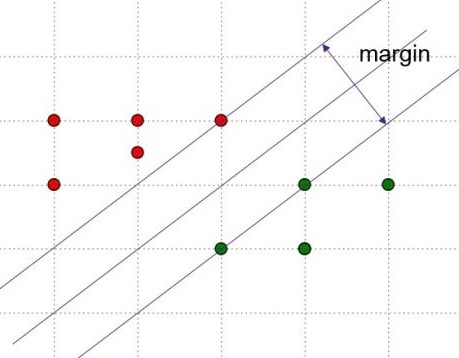
• 假设分类的超平面为(w^Tx+b=0),两个平行的边界超平面分别为

[egin{cases} w^Tx+b=l\ w^Tx+b=-l\ end{cases}]

因为(frac{w}{l}^Tx+frac{b}{l}=0)与(w^Tx+b=0)是同一个超平面,所以等式两边同除以(l),并进行变量替换后,边界超平面可以定义为如下形式:

[egin{cases} w^Tx+b=1\ w^Tx+b=-1\ end{cases}]

• 样本被两个边界超平面分隔开,假设对于标签(y_i=1)的样本,(w^Tx_i+bge 1).则对于标签(y_i=-1)的样本,(w^Tx_i+ble -1).两种情况可以统一为下式:$$y_i(w^Tx_i+b)ge 1$$

• 边界平面(w^Tx+b=1)上任意一点到分类超平面(w^Tx+b=0)的距离为:(d =frac{1}{||w||}),margin为其二倍,等于(frac{2}{||w||}).则SVM求解的过程就是求解(max_wfrac{2}{||w||})的过程,该过程等同于(min_wfrac{1}{2}||w||^2).

• 至此,我们将SVM转换为带有条件约束的最优化问题:

[egin{cases} min_wfrac{1}{2}||w||^2\ y_i(w^Tx_i+b)ge 1\ end{cases}]

3.SVM的求解思路

对于上面带有约束条件的凸优化问题,构造如下拉格朗日函数:

[L(w,b,alpha)=frac{1}{2}||w||^2+sum_{i}alpha_i(1-y_i(w^Tx_i+b)) ]

则原带有约束条件的问题可以等价为(min_{w,b}max_{alpha}L(w,b,alpha)),将min和max互换顺序,得到原问题的对偶问题,(max_{alpha}min_{w,b}L(w,b,alpha)),令( heta(alpha) = min_{w,b}L(w,b,alpha)),则对偶问题可以表示为(max_{alpha} heta(alpha))

因为SVM原问题为凸优化问题,在slater条件满足是,原问题与对偶问题等价,可以通过求解对偶问题得到原问题的最优解(因为KKT条件为强对偶的必要条件,则此时KKT条件必然也是满足的).

求解( heta(alpha)),令(L(w,b,alpha))对(w,b)的偏导数为零:

[egin{cases} frac{partial L(w,b,alpha)}{partial w} = 0\ frac{partial L(w,b,alpha)}{partial b} = 0\ end{cases}]

可以得到(本处省略了具体的求导过程):

[egin{cases} w = sum_{i}alpha_iy_ix_i\ sum_{i}alpha_iy_i = 0\ end{cases}]

将(w,b)带入(L(w,b,alpha))可得( heta(alpha))如下(省略了具体的带入求解过程):

[ heta(alpha) = sum_{i}alpha_i - frac{1}{2}sum_{i,j}alpha_ialpha_jy_iy_jx_i^Tx_j ]

对偶问题最终可以如下表示:

[egin{cases} max_alpha sum_{i}alpha_i - frac{1}{2}sum_{i,j}alpha_ialpha_jy_iy_jx_i^Tx_j\ alpha_i ge 0\ sum_{i}alpha_iy_i = 0\ end{cases}]

(alpha_i ge 0)是拉格朗日因子本身需要满足的条件,(sum_{i}alpha_iy_i = 0)是(L(w,b,alpha))对(b)偏导为0的约束.

求解上式(利用SMO算法,比较复杂本处省略),可以得到最优的一组(alpha_i^*).然后利用(w^* = sum_{i}alpha_i^*y_ix_i)求解得到最优的(w^*).假设(x_+,x_-),分别为两个边界超平面上的点,则(w^*x_++b^*=1),(w^*x_-+b^* = -1),两式相加可得:

[b^* = -frac{w^*x_++w^*x_-}{2} ]

根据KKT条件,(alpha^*_i(y_i(w^*x_i+b)-1)=0),则若(alpha^*_i>0),则(y_i(w^*x_i+b)-1=0),即(x_i)在边界分类超平面上.则求解b过程中的(x_+,x_-)可以在(alpha^*_i>0)的(x_i)中寻找.

4.soft margin的理解

对于线性不可分的样本(有噪声干扰),可以适当放松边界超平面,以得到更好的鲁棒性能.soft margin形式下的SVM定义如下:

[egin{cases} min_{w,b,xi}frac{1}{2}||w||^2+Csum_{i}xi_i\ y_i(w^Tx_i+b)ge 1-xi_i\ xi_ige0 end{cases}]

其中,C为(xi_i)的惩罚因子,C越大,对(xi)的惩罚越大,(xi)的可能取值越小,soft margin效果越弱,鲁棒性能越差,反之亦然.

5.核技巧的理解

核函数能够带来非线性能力,通过将特征映射到高维空间,使得在低维空间中非线性可分的样本在高位空间中线性可分.
SVM对样本分类的判别方法为:(w^Tx+bge0),则(y=1),否则(y=0)
在本文前面分析过程中可到:(w^* = sum_{i}alpha_i^*y_ix_i),带入判别式可得:(sum_{i}alpha_i^*y_ix_i^Tx+bge0),即(sum_{i}alpha_i^*y_i<x_i,x>+bge0).
将上面特征向量的内积换成核函数的内积,即可以得到核函数下SVM的判别表达式:(sum_{i}alpha_i^*y_i<K(x_i),K(x)>+bge0),实际上,在使用核函数时我们并不需要先将特征映射到高维,再在高维进行内积运算,我们往往直接在低维计算出高位内积的结果,这样并没有因维度增加而显著增加计算量.即上式一般改写为:(sum_{i}alpha_i^*y_iK(x_i,x)+bge0).