论文:https://arxiv.org/abs/1801.07698
推荐博客:https://blog.csdn.net/u014380165/article/details/80645489
人脸Reid基础流程如下:

典型的人脸reid算法,对特征提取之后的结构而言,输入xi是1*d的向量,表示输入的特征向量,对该向量执行L2正则化操作就得到xi/||xi||。对该向量W是d*n的矩阵,n表示分类的类别数,因此对每一列(也就是Wj)都执行L2正则化操作,就得到Wj/||Wj||。xi/||xi||和Wj/||Wj||做矩阵相乘得到全连接层的输出,这个输出其实就是cosθj(严格讲是||xi/(||xi||)||*||Wj/(||Wj||)||*cosθj,因为前面两项都是1,所以就是cosθj),其中j属于[1…n]。然后对该输出中对应真实标签的值(cosθyi)执行反余弦操作就能得到θyi,yi就表示真实标签。因为SphereFace、ArcFace和CosineFace中都有m参数,所以这里分别用m1、m2和m3表示,因此这3个算法整合在一起就是cos(m1θyi+m2)-m3。然后乘以一个scale参数s,最后该结果作为以e为底的指数函数的指数送到softmax函数,最后就得到预测的输出概率。
下面讲解下论文中的推导:


Softmax和W-Norm softmax比较简单,坐标轴是cosθ1和cosθ2,分界线的斜率是1。SphereFace中的坐标轴是θ1和θ2,其中class1的线对应Table1中的公式,因为m小于1,cos函数在该输入范围内是递减函数,所以斜率(cosmθ1/cosθ2)大于1。class2那条线同理,同时两条线都过原点。CosinFace中的坐标轴是cosθ1和cosθ2,class1那条线相当于将过原点的斜率为1的线向上平移m的结果,为什么这么说?假设θ2=0,那么class1线就是cosθ1=m,又因为纵坐标轴是cosθ1,因此就是平移m,class2同理。ArchFace中的坐标轴是θ1和θ2,class1这条线相当于将过原点的斜率为1的线向上平移m的结果(注意,虽然都是平移m,但是这里的坐标轴和CosinFace不同,因此平移的量不一样)。
因此这里有个非常重要的结论:在ArcFace中是直接在角度空间(angular space,也就是横纵坐标是角度θ1和θ2,不是softmax或CosineFace中的cosθ1和cosθ2)中最大化分类界限。
话说新版论文似乎没有对为什么ArcFace更好给出具体分析,只是笼统的说对margin设计的微小改动对效能有“蝴蝶效应”般的影响。
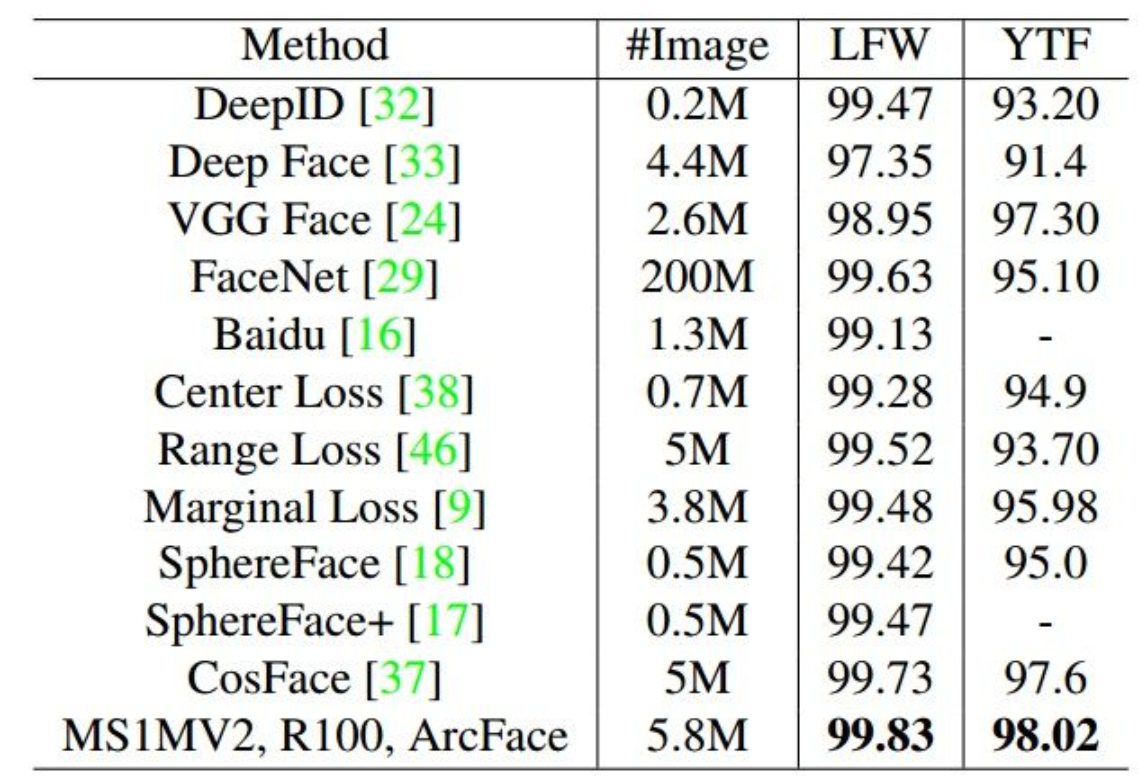
实验比较多,贴个主要的,其他的看原文吧: