题目链接:http://codeforces.com/problemset/problem/549/G
题意:给定一个n个元素的整数序列a[], 任意时刻对于任一对相邻元素a[i-1]、 a[i],若a[i-1] < a[i] 则要依次执行如下两个操作:
1. a[i-1]--, a[i]++;
2. 交换a[i-1]和a[i]的位置。
经过若干次1、2操作后,若能使整个序列变成非降的,则输出最终的序列;否则输出":("。
数据范围:n 属于 [1, 2*10^5], a[i] 属于[0, 10^9]
思路:首先想到交换排序,但n 在10^5所以n^2的排序不可取。后来模拟快排的过程推出了样例,如下:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <queue> 5 #define CLEAR(A, X) memset(A, X, sizeof(A)) 6 #define REP(N) for(int i=0; i<(N); i++) 7 #define REPE(N) for(int i=1; i<=(N); i++) 8 #define FREAD(FN) freopen((FN), "r", stdin) 9 #define pb(a) push_back(a) 10 #define pf() pop_front() 11 using namespace std; 12 13 const int MAX_N = 200005; 14 int n; 15 int a[MAX_N]; 16 int flag; 17 void partition(int s, int e){ 18 if(s == e) return ; 19 int i = s, j = e - 1; 20 //printf("i %d j %d******* ", i, j); 21 while(i < j){ 22 while(i < j && a[j] >= a[i]) j--; 23 if(i < j){ 24 a[j] += j - i; 25 if(a[i] == a[j]){ 26 flag = 1; 27 return ; 28 } 29 a[i] -= j - i; 30 swap(a[i], a[j]); 31 i++; 32 } 33 34 while(i < j && a[i] <= a[j]) i++; 35 if(i < j){ 36 a[i] -= j - i; 37 if(a[i] == a[j]){ 38 flag = 1; 39 return ; 40 } 41 a[j] += j - i; 42 swap(a[i], a[j]); 43 j--; 44 } 45 // for(int k=0; k<n; k++) printf("%d ", a[k]); 46 // printf(" "); 47 }//i == j 48 partition(s, i); 49 partition(i+1, e); 50 } 51 52 int main() 53 { 54 scanf("%d", &n); 55 REP(n) scanf("%d", &a[i]); 56 flag = 0; 57 partition(0, n); 58 if(flag) printf(":( "); 59 else{ 60 REP(n) printf("%d ", a[i]); 61 printf(" "); 62 } 63 return 0; 64 }
但对于第六个test(
5 15 5 8 6 3
)得到的结果是错的,尝试改用i, j 指针同方向走来构造轴点,如下,但还是构造不出正确的结果。

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <queue> 5 #define CLEAR(A, X) memset(A, X, sizeof(A)) 6 #define REP(N) for(int i=0; i<(N); i++) 7 #define REPE(N) for(int i=1; i<=(N); i++) 8 #define FREAD(FN) freopen((FN), "r", stdin) 9 #define pb(a) push_back(a) 10 #define pf() pop_front() 11 using namespace std; 12 13 const int MAX_N = 200005; 14 int n; 15 int a[MAX_N]; 16 int flag; 17 void partition(int s, int e){ 18 if(s == e) return ; 19 int i = s, j = s + 1; 20 int cur = s; 21 //printf("i %d j %d******* ", i, j); 22 while(i < e && j < e){ 23 while(i < j && j < e && a[j] >= a[i]) j++; 24 if(i < j && j < e){ 25 a[j] += j - i; 26 if(a[i] == a[j]){ 27 flag = 1; 28 return ; 29 } 30 a[i] -= j - i; 31 swap(a[i], a[j]); 32 cur = j; 33 i = j + 1; 34 } 35 36 while(j < i && i < e && a[i] >= a[j]) i++; 37 if(j < i && i < e){ 38 a[j] -= i - j; 39 if(a[i] == a[j]){ 40 flag = 1; 41 return ; 42 } 43 a[i] += i - j; 44 swap(a[i], a[j]); 45 cur = j; 46 j = i + 1; 47 } 48 // for(int k=0; k<n; k++) printf("%d ", a[k]); 49 // printf(" "); 50 }//i == j 51 partition(s, cur); 52 partition(cur+1, e); 53 } 54 55 int main() 56 { 57 scanf("%d", &n); 58 REP(n) scanf("%d", &a[i]); 59 flag = 0; 60 partition(0, n); 61 if(flag) printf(":( "); 62 else{ 63 REP(n) printf("%d ", a[i]); 64 printf(" "); 65 } 66 return 0; 67 }
于是看题解了,以下是题解的思路,思想仍是排序,(虽然tag上写了greedy,但我没想明白哪里用到了贪心策略):
由于swap(a[i-1], a[i])时,向左的a[i]在数值上"收益"了1,向右的a[i-1]在数值上"消耗"了1,现在把由交换产生的“收益/消耗”变化量从a[i]的原始数值中分离开来。
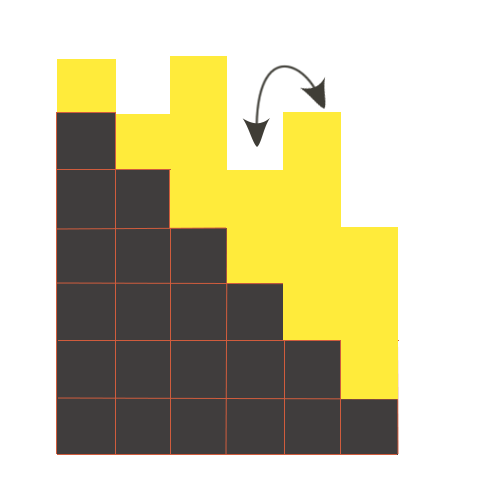
如左图,每一列对应一个位置 i ,其中黑色的“台阶”加上黄色的“塔”为原始的a[i]值,现在规定从左到右台阶的高度从n 均匀递减到 1, 记黄色的塔高 b[i] = 原始高度a[i] - 台阶高度(n - i)(i从0起始);这样每个a[i] 向左交换相当于上一个台阶,向右交换为下一个台阶,对应的塔高b[i]是不变的,如右图。所以我们只需计算出序列b[i]并把它排成非降序,然后再加上对应位置的台阶高度就是最终结果了。对于":("的情况,只需得到结果后扫描一遍检查是否确实非降序即可。

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <queue> 5 #define CLEAR(A, X) memset(A, X, sizeof(A)) 6 #define REP(N) for(int i=0; i<(N); i++) 7 #define REPE(N) for(int i=1; i<=(N); i++) 8 #define FREAD(FN) freopen((FN), "r", stdin) 9 #define pb(a) push_back(a) 10 #define pf() pop_front() 11 using namespace std; 12 13 const int MAX_N = 200005; 14 int n; 15 int a[MAX_N]; 16 int flag; 17 18 int main() 19 { 20 scanf("%d", &n); 21 REP(n) scanf("%d", &a[i]); 22 flag = 0; 23 REP(n) a[i] -= n - i; 24 sort(a, a+n); 25 a[0] += n; 26 for(int i=1; i<n; i++){ 27 a[i] += n - i; 28 if(a[i] < a[i-1]){ 29 flag = 1; 30 break; 31 } 32 } 33 34 if(flag) printf(":( "); 35 else{ 36 REP(n) printf("%d ", a[i]); 37 printf(" "); 38 } 39 return 0; 40 }
