题目描述:
有一个由按钮组成的矩阵,其中每行有6个按钮,共5行。每个按钮的位置上有一盏灯。当按下一个按钮后,该按钮以及周围位置(上边、下边、左边、右边)的灯都会改变一次。
问:给定一组灯的初始状态,求是所有灯都熄灭的解法。
题目分析:
--如果灯原来是点亮的,就会被熄灭;
--如果灯原来是熄灭的,则会被点亮;
--某个灯被按下偶数次则相当于状态并没有改变;
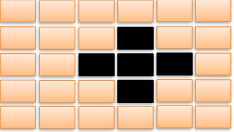
--在矩阵角上的按钮改变3盏灯的状态;
--在矩阵边上的按钮改变4盏灯的状态;
--其他的按钮改变5盏灯的状态。
见下图:


问题实质:枚举
我们可以用最笨拙的办法来求解这个问题,也就是对于这5行6列的灯的矩阵,我们可以设置30重的循环来依次枚举该灯的状态,最终可以求得问题的解,
只是这样虽然可行,但只是针对小规模的灯矩阵才能适用(而且还很耗费计算机的算力)。当然我们会有更好的解决方案,那就是对于一个枚举问题,我们
首先应该想到的是它能否减少枚举次数。熄灯问题中,我们仔细观察便会发现只要我们确定第一行的灯的状态,那么第二行灯的状态也随之确定,同理,第
三行灯的状态也由于第二行灯状态确定而确定......换句话说,当我们确定第一行的灯的状态后(此时,不一定第一行的灯全灭了,还有一些未灭的灯),
我们将第一行中未灭的灯交由第二行灯的按钮来控制使它熄灭,这样第二行灯的按钮状态就由第一行的灯状态而确定了,同理,第三、四行也因此而确定。当
我们需要改变第5行灯的状态来使整个灯矩阵全灭时,前三行的灯都已经熄灭了,第五行灯的按钮状态如果使第四行与第五行灯都熄灭了,那么这组(从第一行
到第五行)按钮的按法就是解。
问题技巧:
很多人在有了思路以后便首先申请了三个二维数组(一个初始灯的状态,一个当前测试开关的灯的状态,一个结果矩阵),但是,仔细考虑后会发现,我们使用
到的数字仅有“0”、“1”,而计算机又是特别擅长处理01串,且我们的各种基本类型都是由二进制来表示的。因此,假设我们申明一个char类型的变量:
char ch;那么就相当于我们有了一个八字节大小的数组(装了8位二进制数)。因此,我们可以申请三个char类型的一维数组,即可存放灯矩阵及结果矩阵。
我们采用位运算即可改变灯按钮的状态。
问题分析即到此,完整代码请看我的专栏 实例代码--熄灯问题。