HDOJ2041_超级楼梯（斐波拉契数列）

正常简单题：通过仔细观察推断即可看出这是一个斐波拉契数列的题目。

HDOJ2041_超级楼梯

在做这题的时候我误入了思维盲区，只想着什么方法可以解决，没有看出是斐波拉契数列。因此第一次用组合数方法打了一次但是WA了，过程中我发现了WA的真正细节（整形数超过范围）还算是有所收获的。

组合数求和解

（WA：因为会炸范围导致M稍微大一些答案就错了）

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>

int main()
{
	int n,i,j,steps;
	scanf("%d",&n);
	for(i=0;i<n;i++)
	{
		unsigned long long sum=0;
		scanf("%d",&steps);
		int max2=(steps-1)/2;//表示最多可以走多少步一次跨两级阶梯
		//循环遍历每一种方法中走0次，1次两阶梯，2次，3次... 
		for(j=0;j<=max2;j++)
		{
			int n1=steps-1-2*j;//改方法中走了多少次跨两级阶梯 
			int n2=j;//该方法中走了多少次跨两级阶梯 
			int stp=n1+n2;
			//计算C(n1+n2,n2)组合数然后叠加即可
			int p,q;
			int sum1=1,sum2=1;
			for(p=1;p<=n2;p++)
			{
				sum1*=(stp--);
				sum2*=p;
			}
			sum+=sum1/sum2;
		}
		printf("%lld
",sum);
	}
	return 0;
}

错误警示：

在对比用斐波拉契数列找出为什么会出错的时候，我随意输入了一串阶梯进行对比，发现在20之前的答案是一致的，但是当M=30时，就出错了，仔细思考意识到代码中使用了累乘，那么整形显然是会爆炸的最后，自然就得不到正确的答案了。计算器摁了一下1乘到13就达到6227020800了，后面炸不炸显而易见。效果如下图

正解

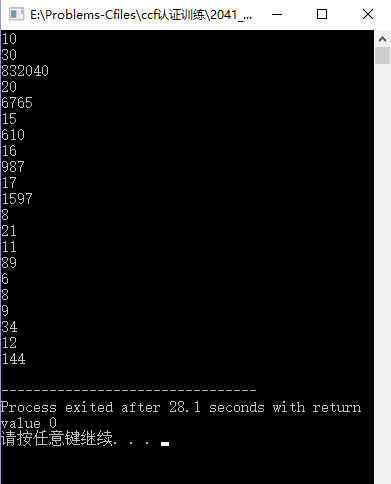
错解

斐波拉契数列求解

观察可得f(1)=0;f(2)=1;f(3)=2;

f(n)=f(n-2)+f(n-1);(n>3时)，这是一道利用斐波拉契数列解的题目。上代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>

int fe[50]={0}; 

int main()
{
	int i,j,n;
	int steps;
	fe[1]=0;fe[2]=1;fe[3]=2;
	for(i=4;i<=41;i++)
	{
		fe[i]=fe[i-1]+fe[i-2];
	}
	scanf("%d",&n);
	for(i=1;i<=n;i++)
	{
		scanf("%d",&steps);
		printf("%d
",fe[steps]);
	}
	return 0;
}