第1章主要内容和教学要求
一、计算机系统
-
计算机系统由硬件、软件组成；
-
指令系统是硬件和软件的界面。
二、计算机语言和程序设计方法
1、 计算机语言
-
程序员与计算机沟通的语言；
-
描述解决问题的方法和相关数据。
2、 计算机语言的级别
-
二进制代码构成的机器语言；
-
使用助记符的汇编语言；
-
使用类似英语单词和语句的高级语言；
-
C++是面向对象的高级语言
3、 C++支持的程序设计方法
-
面向过程的程序设计方法；
-
面向对象的程序设计方法；
-
泛型程序设计方法。
三、C++程序的开发过程
-
算法设计
-
源程序编辑
-
编译
-
连接
-
运行调试
四、信息在计算机中的表示与存储
-
计算机中的数据用二进制表示；
-
逻辑数据、字符数据用二进制编码表示。
学习建议
-
看教学视频；
-
做练习题；
-
完成“实验一”
1.2 计算机系统基本概念
计算机硬件
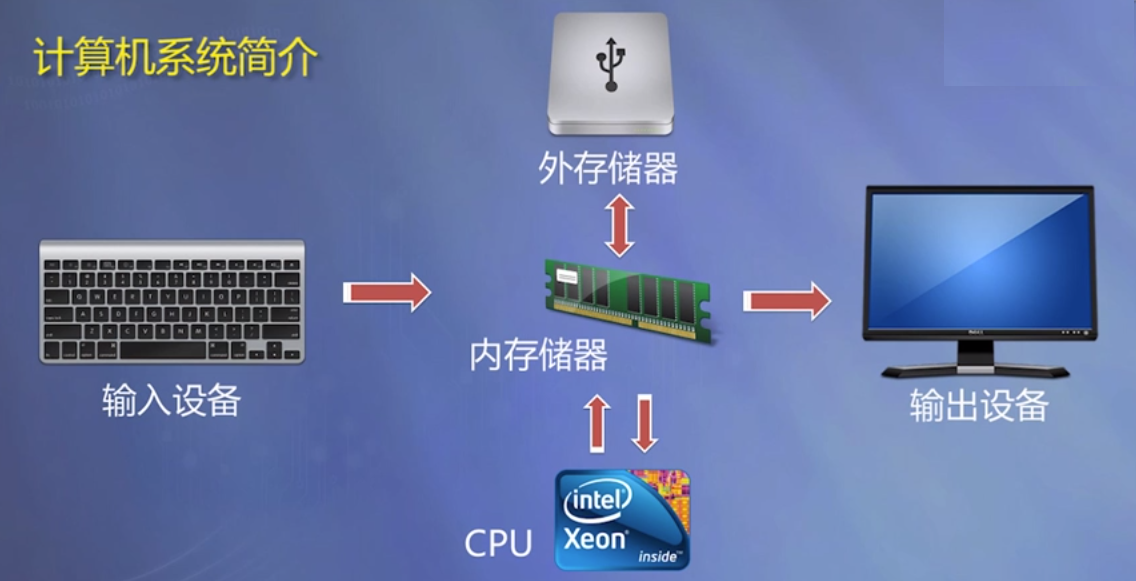
计算程序语言
-
计算机解决问题是程序控制的；
-
程序就是操作步骤；
-
程序要使用语言来表达。
机器语言
-
计算机能识别的是机器语言；
-
机器语言指令是由0和1编码的；
-
例如：
加法指令可能是“0001”。
计算机指令系统
-
机器硬件能够识别的语言（机器语言）的集合；
-
它是软件和硬件的主要界面。
计算软件
-
是一系列按照特定顺序组织的计算机数据和指令的集合。一般来讲软件被划分为系统软件、应用软件和介于这两者之间的中间件；
-
软件包括程序和文档。
计算机程序
-
指令的序列；
-
描述解决问题的方法和数据。
1.3 计算机语言和程序设计方法的发展
计算机语言和程序设计方法
最初的计算机语言——机器语言
-
由二进制代码构成
-
计算机硬件可以识别
-
可以表示简单的操作
-
例如：加法、减法、数据移动等等
汇编语言
- 将机器指令映射为助记符
- 如ADD、SUB、mov 等；
- 抽象层次低，需要考虑机器细节。
高级语言
-
关键字、语句容易理解；
-
有含义的数据命名和算式；
-
抽象层次较高；
- 例如，算式：a+b+c/d
-
屏蔽了机器的细节；
例如，这样显示计算结果：cout<<a+b+c/d
C++语言
-
是高级语言
-
支持面向对象的观点和方法
-
将客观事物看做对象
-
对象间通过消息传送进行沟通
-
支持分类和抽象
-
面向过程的程序设计方法：
-
机器语言、汇编语言、高级语言都支持；
-
最初的目的：用于数学计算；
-
主要工作：设计求解问题的过程。
-
大型复杂的软件难以用面向过程的方式编写
面向对象的程序设计方法：
-
由面向对象的高级语言支持；
-
一个系统由对象构成；
-
对象之间通过消息进行通信。
1.4面向对象的基本概念
对象
-
一般意义上的对象：现实世界中实际存在的事物。
-
面向对象方法中的对象：程序中用来描述客观事物的实体。
抽象与分类
-
分类依据的原则——抽象；
-
抽象出同一类对象的共同属性和行为形成类；
-
类与对象是类型与实例的关系。
封装
-
隐蔽对象的内部细节；
-
对外形成一个边界；
-
只保留有限的对外接口；
-
使用方便、安全性好。
继承
-
意义在于软件复用；
-
改造、扩展已有类形成新的类。
多态
- 同样的消息作用在不同对象上，可以引起不同的行为。
1.5 程序的开发过程
程序
-
源程序：
- 用源语言写的，有待翻译的程序；
-
目标程序：
- 源程序通过翻译程序加工以后生成的机器语言程序 ；
-
可执行程序：
-
连接目标程序以及库中的某些文件，生成的一个可执行文件；
-
例如：Windows系统平台上的.EXE文件。
-
三种不同类型的翻译程序
-
汇编程序：
- 将汇编语言源程序翻译成目标程序；
-
编译程序：
- 将高级语言源程序翻译成目标程序；
-
解释程序：
- 将高级语言源程序翻译成机器指令，边翻译边执行。
C++程序的开发过程
-
算法与数据结构设计；
-
源程序编辑；
-
编译；
-
连接；
-
测试；
-
调试。
1.6计算机中的信息与存储单位
计算机的基本功能
-
算术运算；
-
逻辑运算。
计算机中信息：
-
控制信息——指挥计算机操作；
-
数据信息——计算机程序加工的对象。
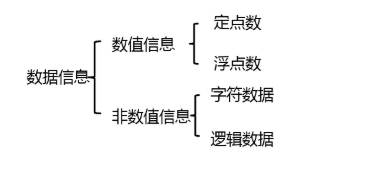
信息的存储单位
-
位(bit，b)：数据的最小单位，表示一位二进制信息；
-
字节(byte，B)：八位二进制数字组成(1 byte = 8 bit)；
-
千字节 1 KB = 1024 B；
-
兆字节 1 MB = 1024 K；
-
吉字节 1 GB = 1024 M。
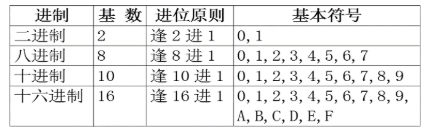
计算机的数字系统
计算机的数字系统
-
二进制系统；
-
基本符号：0、1。
程序中常用的数制:
R 进制转换为十进制:
- 各位数字与它的权相乘，其积相加，例如:
(11111111.11)2 =1×27+1×26+1×25+1×24+1×23+1×22+1×21+1×20+1×2-1+1×2-2 =(255.75)10
十进制整数转换为R 进制整数：
- “除以R取余”法。
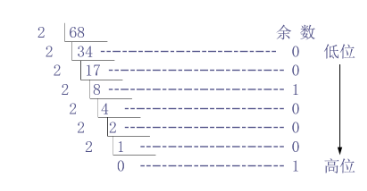所以 6810＝10001002
十进制小数→ R 进制小数：
- “乘 以R 取整”法。
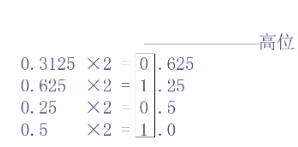所以 0.312510 = 0.01012
二、八、十六进制的相互转换
-
1位八进制数相当于3位二进制数；
-
1位十六进制数相当于4位二进制数，例如：
((1011010.10)_{2}=(001 011 010 .100)_2=(132.4)_8)
((1011010.10)_{2}=(0101 1010 .1000)_{2}=(5A8)_{16})
((F 7)_{16}＝(1111 0111)_2＝(11110111)_2)
数据在计算机中的编码表示
二进制数的编码表示
-
需要解决的问题：负数如何表示？
-
最容易想到的方案：
0：表示“+”号；
1：表示“-”号。
-
原码
- “符号──绝对值”表示的编码
例如：
- 原码的缺点：
- 零的表示不惟一
[+0]原 =000...0
[-0]原 =100...0
- 进行四则运算时，符号位须单独处理，运算规则复杂。
-
补码
-
符号位可作为数值参加运算；
-
减法运算可转换为加法运算；
-
0的表示唯一。
-
-
补码的原理
-
模数：
n位二进制整数的模数为 2n ；
n位二进制小数的模数为 2。
-
补数：
-
一个数减去另一个数（加一个负数），等于第一个数加第二个数的补数，例（时钟指针）： 8+(-2)=8+10 ( mod 12 )=6；
-
一个二进制负数可用其模数与真值做加法 (模减去该数的绝对值) 求得其补码，例（时钟指针）：-2+12=10。
-
-
-
补码的计算
-
借助于“反码”作为中间码；
-
负数的反码与原码有如下关系：
符号位不变(仍用1表示)，其余各位取反(0变1，1变0)，例如：
X=-1100110 [X]原 =1 1100110 [X]反 =1 0011001 -
正数的反码与原码表示相同，正数的补码与原码相同；
-
反码只是求补码时的中间码；
-
负数的补码由该数反码的末位加 1 求得。
-
对补码再求补即得到原码。
-
-
补码的优点：
-
0的表示唯一；
-
符号位可作为数值参加运算；
-
补码运算的结果仍为补码。
-
实数的浮点表示
-
计算机中通常采用浮点方式表示小数；
-
实数 N 用浮点形式可表示为： N=M×2E
E：2的幂，N：阶码；
M：N的尾数。
字符在计算机中的表示
-
字符在计算机中是通过编码表示的；
-
例如：
ASCII码是一种常用的西文字符编码：用7位二进制数表示一个字符，最多可以表示27=128个字符;
-
《GB 18030-2005 信息技术 中文编码字符集》是中国国家标准。