前言
堆排序我是看了好半天别人的博客才有了理解,然后又费了九牛二虎之力才把代码写出来,我发现我的基础真的很差劲啊……不过自己选的路一定要坚持走下去。
我试着把我的理解描述出来,如有不妥之处希望大家可以指点出来
算法说明
堆排序,是基于堆的排序。 堆也就是二叉树的一种(完全二叉树),首先要确定堆的定义,才可以学会堆算法的逻辑;
OK,我们知道堆的定义前得先确定啥是完全二叉树。
二叉树就是树状结构是这样的,如图:
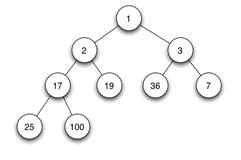
通常二叉树都会存放在数组中,那么将上图的完全二叉树放在数组中就是int[] arrayData = {1,2,3,17,19,36,7,25,100}
然后还有一个前置知识要知道,就是如何计算左子孩子的索引和右子孩子的索引。
还是以上图来举例子,3,36,7这三个数中, 3就是父节点,36 和 7就是子节点。 然后左子节点和右子节点的计算公式是i*2+1 和 i*2+2 。 替换到我举的例子中就是,数字3在数组中的索引是2,那么根据公式所述,左子节点的数组索引是2*2+1=5,右子节点的数组索引是2*2+2=6。 大家可以对一下数字36和数字7的数组索引和我们计算出来的是否一致。
还有,父节点的索引公式是 (i-1)/2。 大家可以代入一下上面的数组求一下值
OK,下面我们可以看一下堆的定义了。
堆的定义是这样的:

如图,堆分两种,一种是“小顶堆”,另一种是“大顶堆“。
小顶堆:就是顶点是最小值,并且父节点小于等于左子节点和右子节点(子节点公式上边有说)
大顶堆:就是顶点是最大值,并且父节点大于等于左子节点呼右子节点(子节点公式上边有说)
OK,现在说一下堆排序的逻辑。 堆排序是有两步:
第一步:建立堆。 我们需要把无序数组调整成堆结构(也就是让无序数组满足上图的条件)
大概过程,如图:
如图如所,我们要建立的是小顶堆,所以父节点一定是大小子节点的。
那么从97这个数字开始,是才有子节点的。 如果按公式来算,就是索引第(i/2)-1个数字是第一个有子节点的数字。
比较完数字97,把小的数字与97对换,然后再比较数字65与65子节点大小,然后再比较数字38与38子节点大小,最终比较最顶节点与子节点。
OK,有一个槽点要注意,请大家看第四图和第五图,当比较顶节点和子节点时,13与49换了位置,这时发现换位置后的49与49子节点是不满足堆的关联,所以49与27也要做一下互换的。 大家有个印象就行,具体逻辑还是请看下边的代码(17行至20行)
第二步:进行堆排序。
因为堆其实就是一个数组,所以如果我们的堆是完全从小到大,或者从大到小存储数据,那么数组同样也就是升序,或者降序了。
以下代码第24行至31行是进行堆排序。
我们可以看到我们之前代码建立好的堆是小顶堆,也就是最小值是在顶点。
第26行到28行,做的就是把第一个节点与最后一个节点数字互换,这时,最小值就在最后边了。
然后执行第30行的代码,因为上边把节点数字做了互换,这时堆就变成了无序数组,那么需要重新建立堆啦,需要把第一个节点至(最后一个节点-1)进行重建堆。
重建堆后,最小的数字又会放到第一他节点啦
接着执行第26行到28行,把第一个节点与(最后一个节点-1)数字互换,这时,最小值就在(最后一个节点-1)了。
然后执行第30行代码,继续重新建立堆。。。。如此类推,数字将会进行降序。
代码
使用JAVA
/*
* 堆排序
*/
public class HeadSort {
public static void main(String[] args) {
int[] arrayData = { 5, 9, 6, 7, 4, 1, 2, 3, 8 };
HeadSortMethod(arrayData);
for (int integer : arrayData) {
System.out.print(integer);
System.out.print(" ");
}
}
public static void HeadSortMethod(int[] arrayData) {
// 第一步,将无序数组,建成一个堆。
//System.out.println("开始建堆");
for (int i = arrayData.length / 2 - 1; i >= 0; i--) {
// 第一个有孩子节点的节点,索引是arrayData.length/2-1 。 这个就不证明了(暂时还不会),大家测试一下就知道结果了
HeadAjust(arrayData, i, arrayData.length);
}
//System.out.println("开始排序");
// 第二步,进行排序
// 对堆进行递归,来建立排好序的堆。
int temp;
for (int i = arrayData.length-1; i > 0; i--) {
temp = arrayData[0];
arrayData[0] = arrayData[i];
arrayData[i] = temp;
HeadAjust(arrayData, 0, i - 1);
}
}
/*
* 对于指定数组的序列,进行堆化调整 也就是将无序数组调整成堆。
*/
public static void HeadAjust(int[] arrayData, int beginIndex, int endIndex) {
int minNum = arrayData[beginIndex];
// i=beginIndex*2+1代表是左子节点
// i=i*2+1代表下一个左子节点
for (int i = beginIndex * 2 + 1; i <= endIndex; i = i * 2 + 1) {
//System.out.println(i);
// 先比较左子节点和右子节点, i存储小值的索引
if (i < endIndex && arrayData[i] > arrayData[i + 1]) {
i++;
}
if (arrayData[i] > minNum) {
break;
}
arrayData[beginIndex] = arrayData[i];
beginIndex = i;
}
arrayData[beginIndex] = minNum;
}
}
执行结果:
9 8 7 6 5 4 3 2 1
时间复杂度:O(nlog2n) 参考这里http://blog.csdn.net/liliuteng/article/details/8496050, 说实在的,这个证明过程我还是看不太懂……数学基础不太好,过后需要再学习一下数学了。
空间复杂度:O(1)
学习资料
http://blog.csdn.net/clam_clam/article/details/6799763 本次总结大部分图是从这里来的…实在是懒着画了,抱歉抱歉
http://www.cnblogs.com/mengdd/archive/2012/11/30/2796845.html