算法思路
问题
给定顶点集合为 V,边集合为 E,求最小生成树 T?
解过程
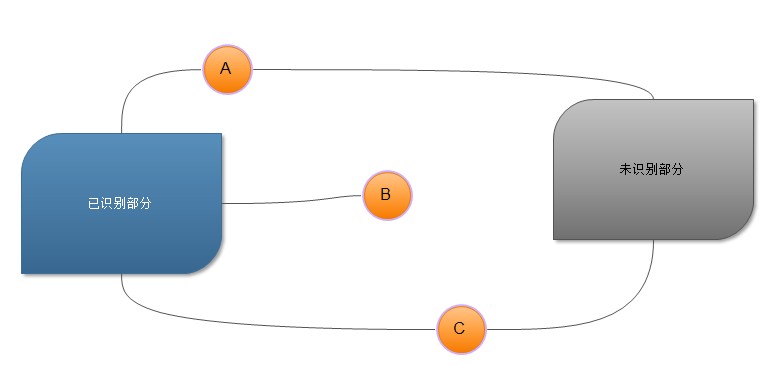
任意时刻的边都可以划分为到三个集合:
- X:边的所有顶点都是最小生成树的一部分。
- Y:边的末端节点不是最小生成树的一部分。
- Z:其它。
从 Y 中选择权重最小的边,将其加入到 T 中。
优先级队列
该算法需要用到一个工具:优先级队列(从某个集合中选择最小的元素)。
1 class PriorityQueue<T> 2 where T : IComparable<T> 3 { 4 private T[] _items; 5 private int _length; 6 7 public PriorityQueue(int size) 8 { 9 _items = new T[size]; 10 } 11 12 public void EnQueue(T item) 13 { 14 if (this.IsFull()) 15 { 16 throw new InvalidOperationException("容量已满,不能插入!"); 17 } 18 19 _items[_length++] = item; 20 this.MoveUp(_length - 1); 21 } 22 23 private void MoveUp(int index) 24 { 25 var bottom = _items[index]; 26 var current = index; 27 28 while (current > 0) 29 { 30 var parent = (current - 1) / 2; 31 if (_items[parent].CompareTo(bottom) < 0) 32 { 33 break; 34 } 35 36 _items[current] = _items[parent]; 37 current = parent; 38 } 39 40 _items[current] = bottom; 41 } 42 43 public T DeQueue() 44 { 45 if (this.IsEmpty()) 46 { 47 throw new InvalidOperationException("容量已空,不能删除!"); 48 } 49 50 var result = _items[0]; 51 _items[0] = _items[--_length]; 52 53 this.MoveDown(0); 54 55 return result; 56 } 57 58 private void MoveDown(int index) 59 { 60 var top = _items[index]; 61 var current = index; 62 63 while (current < _length) 64 { 65 var small = 0; 66 var left = 2 * current + 1; 67 var right = left + 1; 68 69 if (left < _length && right < _length) 70 { 71 if (_items[left].CompareTo(_items[right]) <= 0) 72 { 73 small = left; 74 } 75 else 76 { 77 small = right; 78 } 79 } 80 else if (left < _length) 81 { 82 small = left; 83 } 84 else 85 { 86 break; 87 } 88 89 if (_items[small].CompareTo(top) >= 0) 90 { 91 break; 92 } 93 94 _items[current] = _items[small]; 95 current = small; 96 } 97 98 _items[current] = top; 99 } 100 101 public bool IsFull() 102 { 103 return _length == _items.Length; 104 } 105 106 public bool IsEmpty() 107 { 108 return _length == 0; 109 } 110 }
最小生成树代码
1 class Edge : IComparable<Edge> 2 { 3 public int StartIndex { get; set; } 4 5 public int EndIndex { get; set; } 6 7 public int Weight { get; set; } 8 9 public string Description { get; set; } 10 11 public int CompareTo(Edge other) 12 { 13 return this.Weight.CompareTo(other.Weight); 14 } 15 } 16 17 private class Path : IComparable<Path> 18 { 19 public Path() 20 { 21 this.Edges = new List<Edge>(); 22 } 23 24 public int StartVertexIndex { get; set; } 25 26 public int EndVertexIndex { get; set; } 27 28 public List<Edge> Edges { get; private set; } 29 30 public int Weight { get; private set; } 31 32 public void AddEdges(IEnumerable<Edge> edges) 33 { 34 foreach (var edge in edges) 35 { 36 this.AddEdge(edge); 37 } 38 } 39 40 public void AddEdge(Edge edge) 41 { 42 this.Edges.Add(edge); 43 this.Weight += edge.Weight; 44 } 45 46 public int CompareTo(Path other) 47 { 48 return this.Weight.CompareTo(other.Weight); 49 } 50 } 51 52 class Vertex<T> 53 { 54 public T Value { get; set; } 55 } 56 57 class Graph<T> 58 { 59 #region 私有字段 60 61 private int _maxSize; 62 private Vertex<T>[] _vertexs; 63 private Edge[][] _edges; 64 private int _vertexCount = 0; 65 66 #endregion 67 68 #region 构造方法 69 70 public Graph(int maxSize) 71 { 72 _maxSize = maxSize; 73 _vertexs = new Vertex<T>[_maxSize]; 74 _edges = new Edge[_maxSize][]; 75 for (var i = 0; i < _maxSize; i++) 76 { 77 _edges[i] = new Edge[_maxSize]; 78 } 79 } 80 81 #endregion 82 83 #region 添加顶点 84 85 public Graph<T> AddVertex(T value) 86 { 87 _vertexs[_vertexCount++] = new Vertex<T> { Value = value }; 88 89 return this; 90 } 91 92 #endregion 93 94 #region 添加边 95 96 public Graph<T> AddUnDirectedEdge(T startItem, T endItem, int weight) 97 { 98 var startIndex = this.GetVertexIndex(startItem); 99 var endIndex = this.GetVertexIndex(endItem); 100 101 _edges[startIndex][endIndex] = new Edge { StartIndex = startIndex, EndIndex = endIndex, Weight = weight, Description = String.Format("{0}->{1}", startItem, endItem) }; 102 _edges[endIndex][startIndex] = new Edge { StartIndex = endIndex, EndIndex = startIndex, Weight = weight, Description = String.Format("{0}->{1}", endItem, startItem) }; 103 104 return this; 105 } 106 107 public Graph<T> AddDirectedEdge(T startItem, T endItem, int weight) 108 { 109 var startIndex = this.GetVertexIndex(startItem); 110 var endIndex = this.GetVertexIndex(endItem); 111 112 _edges[startIndex][endIndex] = new Edge { StartIndex = startIndex, EndIndex = endIndex, Weight = weight, Description = String.Format("{0}->{1}", startItem, endItem) }; 113 114 return this; 115 } 116 117 #endregion 118 119 #region 最小生成树 120 121 public IEnumerable<Edge> GetMinimumSpanningTree() 122 { 123 var minimumSpanningTrees = new List<Edge>(); 124 Dictionary<int, bool> vertexInTreesTracker = new Dictionary<int, bool>(); 125 var queue = new PriorityQueue<Edge>(_maxSize); 126 127 var currentVertexIndex = 0; 128 while (minimumSpanningTrees.Count < _vertexCount - 1) 129 { 130 vertexInTreesTracker[currentVertexIndex] = true; 131 132 foreach (var item in _edges[currentVertexIndex]) 133 { 134 if (item == null) 135 { 136 continue; 137 } 138 if (vertexInTreesTracker.ContainsKey(item.EndIndex)) 139 { 140 continue; 141 } 142 143 queue.EnQueue(item); 144 } 145 146 var smallEdge = queue.DeQueue(); 147 while (vertexInTreesTracker.ContainsKey(smallEdge.EndIndex)) 148 { 149 smallEdge = queue.DeQueue(); 150 } 151 minimumSpanningTrees.Add(smallEdge); 152 currentVertexIndex = smallEdge.EndIndex; 153 } 154 155 return minimumSpanningTrees; 156 } 157 158 #endregion 159 160 #region 最短路径 161 162 public IEnumerable<Edge> GetShortestPath(T startItem, T endItem) 163 { 164 var startIndex = this.GetVertexIndex(startItem); 165 var endIndex = this.GetVertexIndex(endItem); 166 167 var shortestPaths = new Dictionary<int, Path>(); 168 var queue = new PriorityQueue<Path>(_maxSize); 169 170 var currentVertexIndex = startIndex; 171 var currentPath = new Path 172 { 173 StartVertexIndex = startIndex, 174 EndVertexIndex = endIndex 175 }; 176 177 while (!shortestPaths.ContainsKey(endIndex)) 178 { 179 foreach (var item in _edges[currentVertexIndex]) 180 { 181 if (item == null) 182 { 183 continue; 184 } 185 if (shortestPaths.ContainsKey(item.EndIndex)) 186 { 187 continue; 188 } 189 190 var path = new Path 191 { 192 StartVertexIndex = startIndex, 193 EndVertexIndex = item.EndIndex 194 }; 195 path.AddEdges(currentPath.Edges); 196 path.AddEdge(item); 197 queue.EnQueue(path); 198 } 199 200 var smallPath = queue.DeQueue(); 201 while (shortestPaths.ContainsKey(smallPath.EndVertexIndex)) 202 { 203 smallPath = queue.DeQueue(); 204 } 205 shortestPaths[smallPath.EndVertexIndex] = smallPath; 206 currentVertexIndex = smallPath.EndVertexIndex; 207 currentPath = smallPath; 208 } 209 210 return shortestPaths[endIndex].Edges; 211 } 212 213 #endregion 214 215 #region 帮助方法 216 217 private int GetVertexIndex(T item) 218 { 219 for (var i = 0; i < _vertexCount; i++) 220 { 221 if (_vertexs[i].Value.Equals(item)) 222 { 223 return i; 224 } 225 } 226 return -1; 227 } 228 229 #endregion 230 }
备注
最短路径的算法和最小生成树的算法非常相似,都是利用了:优先级队列。