队列是先进先出的线性表,顾名思义,优先队列则是元素有优先级的队列,出列的顺序由元素的优先级决定。从优先队列中删除元素是根据优先权的高低次序,而不是元素进入队列的次序。优先队列的典型应用是机器调度等。
假设我们对机器服务进行收费。每个用户每次使用机器所付费用都是相同的,但每个用户所需要服务时间都不同。为获得最大利润,假设只要有用户机器就不会空闲,我们可以把等待使用该机器的用户组织成一个最小优先队列,优先权即为用户所需服务时间。当一个新的用户需要使用机器时,将他 /她的请求加入优先队列。一旦机器可用,则为需要最少服务时间(即具有最高优先权)的用户提供服务。如果每个用户所需时间相同,但用户愿意支付的费用不同,则可以用支付费用作为优先权,一旦机器可用,所交费用最多的用户可最先得到服务,这时就要选择最大优先队列。
1.概念
优先队列( priority queue)是0个或多个元素的集合,每个元素都有一个优先权或值,对优先队列执行的操作有 1) 查找; 2) 插入一个新元素; 3) 删除。在最小优先队列( min priority q u e u e)中,查找操作用来搜索优先权最小的元素,删除操作用来删除该元素;对于最大优先队列( max priority queue),查找操作用来搜索优先权最大的元素,删除操作用来删除该元素。优先权队列中的元素可以有相同的优先权,查找与删除操作可根据任意优先权进行。
描述优先队列最简单的方法是采用无序线性表。假设有一个具有n个元素的优先队列,如果采用公式化的线性表描述,那么插入操作可以十分方便的在表的右端末尾执行,插入操作的时间为O(1)。删除时必须查找优先权最大的元素,因此所需时间为O(n)。
若采用有序的线性表,则插入为O(n),删除为O(1)
2.实现
由上面描述可以知道,我们可以在线性表的基础上完成优先队列,只需要改变删除的操作,当删除时找到最大或最小的值即可。
我们可以直接继承线性表类线性表的2种实现方式:数组和链表
线性表的公式化实现:

1 #ifndef LINEARLIST_H 2 #define LINEARLIST_H 3 #include<iostream> 4 #include<cstdlib> 5 #include<new> 6 using std::cout; 7 using std::endl; 8 template<class T> 9 class LinearList 10 { 11 public: 12 LinearList(int MaxListSize=10);//构造函数 13 virtual ~LinearList(); 14 bool IsEmpty()const 15 { 16 return length==0; 17 } 18 int Length()const {return length;} 19 bool Find(int k,T& x)const;//返回第K个元素到中 20 int Search(T& x)const;//返回x的位置 21 LinearList<T>& Delete(int k,T& x);//删除位置k的元素,并将元素值存到x 22 LinearList<T>& Insert(int k,const T& x);//将x插入到k位置之后 23 void Output(std::ostream& out)const;//输出到流 24 25 protected: 26 int length;//线性表当前长度 27 int MaxSize;//最大长度 28 T *element;//线性表数组 29 }; 30 31 class NoMem 32 { 33 public : 34 NoMem(){ 35 cout<<"No Memory"<<endl; 36 //std::exit(1); 37 } 38 39 }; 40 41 class OutofBounds 42 { 43 public : 44 OutofBounds() 45 { 46 cout<<"Out of Bounds"<<endl; 47 //std::exit(1); 48 } 49 }; 50 51 52 void my_new_handler() 53 { 54 throw NoMem(); 55 } 56 57 template<class T> 58 LinearList<T>::LinearList(int MaxListSize) 59 { 60 std::new_handler old_Handler=std::set_new_handler(my_new_handler); 61 MaxSize=MaxListSize; 62 element=new T[MaxSize]; 63 length=0; 64 65 } 66 67 template<class T> 68 LinearList<T>::~LinearList() 69 { 70 delete[]element; 71 MaxSize=0; 72 length=0; 73 } 74 75 template<class T> 76 bool LinearList<T>::Find(int k,T&x)const 77 { 78 if(k<0||k>length) 79 return false; 80 x=element[k-1]; 81 return true; 82 } 83 84 template<class T> 85 int LinearList<T>::Search(T &x)const 86 { 87 int i=0; 88 while(i<length&&element[i]!=x) 89 { 90 i++; 91 } 92 if(i==length) return 0; 93 else return i+1; 94 } 95 96 template<class T> 97 LinearList<T>& LinearList<T>::Delete(int k,T &x) 98 { 99 if(Find(k,x))//存在位置k 100 { 101 for(int i=k;i<length;++i) 102 { 103 element[i-1]=element[i];//k之后元素向前移动一位 104 } 105 length--; 106 return *this; 107 } 108 else 109 { 110 throw OutofBounds(); 111 } 112 } 113 114 template<class T> 115 LinearList<T>& LinearList<T>::Insert(int k,const T &x) 116 { 117 if(k<0||k>length) 118 { 119 throw OutofBounds(); 120 } 121 else if(length==MaxSize) 122 { 123 throw NoMem(); 124 } 125 else 126 { 127 for(int i=length;i>k;--i) 128 { 129 element[i]=element[i-1];//k之后元素向后移动一位 130 } 131 element[k]=x; 132 length++; 133 return *this; 134 } 135 } 136 137 template<class T> 138 void LinearList<T>::Output(std::ostream& out)const 139 { 140 for(int i=0;i<length;i++) 141 { 142 143 out<<element[i]<<" "; 144 } 145 } 146 147 template<class T> 148 std::ostream& operator<<(std::ostream &out,const LinearList<T>& x) 149 { 150 x.Output(out); 151 return out; 152 } 153 154 #endif // LINEARLIST_H
最大优先队列:

1 #ifndef PRIORITYQUEUE_H 2 #define PRIORITYQUEUE_H 3 #include "LinearList.h" 4 5 template<typename T> 6 class PriorityQueue:public LinearList<T> 7 { 8 public: 9 PriorityQueue(int MaxListSize=10):LinearList<T>::LinearList(MaxListSize){}; 10 PriorityQueue<T>& Insert(const T& x); 11 PriorityQueue<T>& Delete(T& x); 12 T Max() const; 13 ~PriorityQueue(){}; 14 //void Output(std::ostream& out)const;//输出到流 15 friend ostream& operator<< <>(ostream& output, const PriorityQueue<T>& x); 16 private: 17 size_t MaxIndex() const; 18 19 }; 20 21 //末端插入 22 template<typename T> 23 PriorityQueue<T>& PriorityQueue<T>::Insert(const T& x) 24 { 25 if (length>=MaxSize) 26 { 27 throw NoMem(); 28 } 29 30 element[length++] = x; 31 return *this; 32 } 33 34 //找到最大值的索引(下标) 35 template<typename T> 36 size_t PriorityQueue<T>::MaxIndex() const 37 { 38 if (length == 0) 39 { 40 throw OutofBounds(); 41 } 42 size_t maxNum = 0; 43 for (size_t i = 1; i < length; ++i) 44 { 45 if (element[i]>element[maxNum]) 46 { 47 maxNum = i; 48 } 49 } 50 51 return maxNum; 52 } 53 54 //返回最大值 55 template<typename T> 56 T PriorityQueue<T>::Max() const 57 { 58 if (length==0) 59 { 60 throw OutofBounds(); 61 } 62 size_t maxNum = MaxIndex(); 63 64 return element[maxNum]; 65 } 66 67 //取出最大值 68 template<typename T> 69 PriorityQueue<T>& PriorityQueue<T>::Delete(T& x) 70 { 71 if (length==0) 72 { 73 throw OutofBounds(); 74 } 75 76 size_t maxindex = MaxIndex(); 77 x = element[maxindex]; 78 79 //元素前移 80 for (size_t i = maxindex; i < length-1;++i) 81 { 82 element[i] = element[i + 1]; 83 } 84 --length; 85 return *this; 86 } 87 /* 88 template<typename T> 89 void PriorityQueue<T>::Output(std::ostream& out) const 90 { 91 if (length==0) 92 { 93 throw OutofBounds(); 94 } 95 for (size_t i = 0; i < length;++i) 96 { 97 out << element[i]<<' '; 98 } 99 100 out << endl; 101 } 102 */ 103 template<typename T> 104 ostream& operator<<(ostream& output,const PriorityQueue<T>& x) 105 { 106 x.Output(output); 107 return output; 108 } 109 #endif
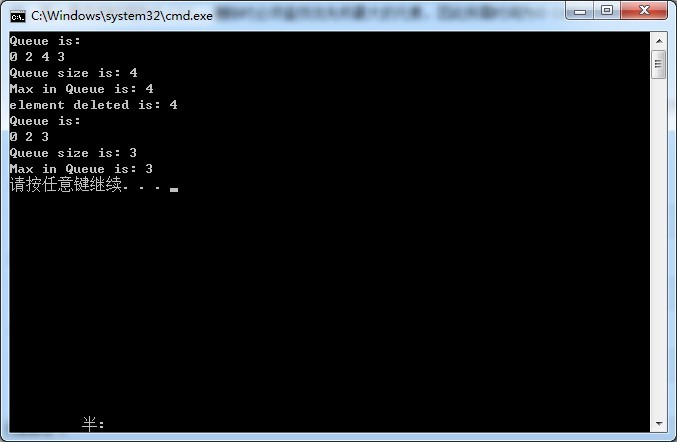
测试:

1 #include<iostream> 2 using namespace std; 3 4 #include "PriorityQueue.h" 5 6 int main() 7 { 8 PriorityQueue<int> testQ; 9 testQ.Insert(0); 10 testQ.Insert(2); 11 testQ.Insert(4); 12 testQ.Insert(3); 13 14 cout << "Queue is: " << endl; 15 cout << testQ << endl; 16 cout << "Queue size is: " << testQ.Length(); 17 cout << endl; 18 cout << "Max in Queue is: " << testQ.Max(); 19 cout << endl; 20 21 int x; 22 testQ.Delete(x); 23 cout << "element deleted is: " << x<<endl; 24 25 cout << "Queue is: " << endl; 26 cout << testQ << endl; 27 cout << "Queue size is: " << testQ.Length(); 28 cout << endl; 29 cout << "Max in Queue is: " << testQ.Max(); 30 cout << endl; 31 32 return 0; 33 }